单筋矩形截面梁正截面承载力计算方法

（一）计算简图

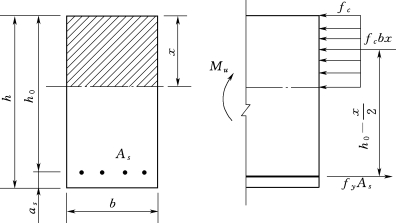
图2-17　单筋矩形截面梁正截面承载力计算简图

根据受弯构件适筋破坏的特征，在进行单筋矩形截面受弯承载力计算时，忽略受拉区混凝土的作用；受压区混凝土的应力图形采用等效矩形应力图形，应力值达到混凝土的轴心抗压强度设计值fc；受拉钢筋应力达到其抗拉强度设计值fy。计算简图如图2-17所示。

（二）基本公式

根据计算简图（图2-17），由截面内力的平衡条件，并满足承载能力极限状态设计表达式的要求，可得出两个基本计算公式，即

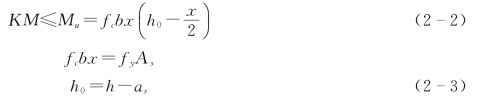
式中　M——弯矩设计值，N·mm；

　　　K——承载力安全系数，按表1-12取用；

　　　fc——混凝土轴心抗压强度设计值，N/mm2，按表1-7取用；

　　　b——矩形截面宽度，mm；

　　　x——混凝土受压区计算高度，mm；

　　　h0——截面有效高度，mm；

　　　h——截面高度；

　　　as——纵向受拉钢筋合力点至截面受拉边缘的距离；

　　　fy——钢筋抗拉强度设计值，N/mm2，按表1-4取用；

　　　As——受拉区纵向钢筋截面面积，mm2。

在式（2-2）和式（2-3）中，是假定受拉钢筋的应力达到fy，受压混凝土的应力达到fc的。这种应力状态只在配筋量适中的构件中才会发生，所以基本公式只适用于适筋梁，而不适用于超筋梁和少筋梁。应用基本公式时应满足下面两个适用条件，即

式中　ξb——相对界限受压区计算高度，对于热轧钢筋，按表2-5取用；

　　　ρ——受拉区纵向钢筋配筋率；

　　　ρmin——受弯构件纵向受拉钢筋最小配筋率，按附录C取用。

式（2-4）是为了防止配筋过多而发生超筋破坏，式（2-5）是为了防止配筋过少而发少筋破坏。

按式（2-2）和式（2-3），在已知材料强度、截面尺寸等条件下，可联立解出受压区高及受拉钢筋截面面积值，但比较麻烦。为了计算方便，可将式（2-2）及式（2-3）改如下。

将ξ=x/h0（即x=ξh0）代入式（2-2）、式（2-3），并令

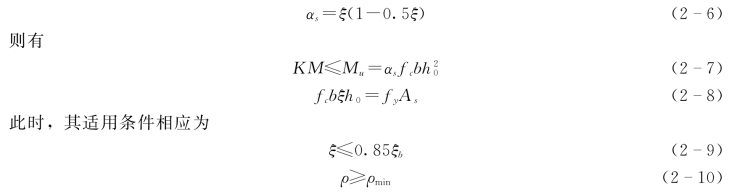
（三）基本公式应用

钢筋混凝土受弯构件的正截面承载力计算有截面设计和承载力复核两种情况。

1.截面设计

截面设计时，一般可先根据建筑物使用要求、外荷载（弯矩设计值）大小及所选用的混凝土与钢筋等级，凭设计经验或参考类似结构确定构件的截面尺寸b及h，然后计算受拉钢筋截面面积As。

在设计中，可有多种不同截面尺寸的选择。显然，截面尺寸定得大，配筋率ρ就可小一些；截面尺寸定得小，配筋率ρ就会大一些。截面尺寸的选择应使计算得出的配筋率ρ处在常用配筋率范围之内。矩形截面梁常用配筋率范围为0.6%～1.5%，T形截面梁常用配筋率范围为0.9%～1.8%。应当指出的是，对于有特殊使用要求的构件，其配筋率则应灵活处理。比如，为了减轻预制构件的自重，有时采用比常用配筋率略高的数值；对于有抗裂要求的构件，其配筋率将低于上述数值。

正截面抗弯配筋计算步骤如下。

（1）作出梁的计算简图（图2-18）。计算简图中应标明计算跨度、支座和荷载的情况。

计算跨度l0可取下列数值的较小者。

对于简支梁，有

式中　ln——梁的净跨度，mm；

　　　a——梁的支承长度，mm。

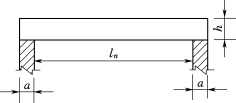
图2-18　梁的计算简图

（2）计算设计弯矩值M。

对于简支梁，按作用在梁上的全部荷载（永久荷载及可变荷载），求出跨中最大弯矩设计值。对于外伸梁，则应根据荷载最不利组合，分别求出简支梁跨跨中最大正弯矩和支座最大负弯矩设计值。

（3）配筋计算。

第一步：由式（2-7）计算αs，即

第二步：按式（2-6）求ξ，并验算是否满足式（2-9）。若不满足，说明截面尺寸过小，可能发生超筋破坏，则应加大截面尺寸、提高混凝土强度等级或采用双筋截面重新设计。

第三步：由式（2-8）计算出所需要的钢筋截面面积As，即

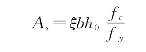
第四步：计算配筋率ρ=As/（bh0），并检查是否满足适用条件式（2-10）。若不满足，则应按最小配筋率ρmin配筋，即取As=ρminbh0，或减小截面尺寸重新设计。(www.xing528.com)

最好使求得的ρ处在常用配筋率范围内，若不在常用配筋率范围内，可修改截面尺寸，重新计算，经过一两次计算后，就能够确定出合适的截面尺寸和钢筋数量。

第五步：由附录A选择合适的钢筋直径及根数。实际采用的钢筋截面面积一般应等于或略大于计算所需的钢筋截面面积，若小于计算所需要的面积，则两者相差不应超过5%。钢筋的直径和间距等应符合有关构造规定。

（4）绘制截面配筋图。

截面配筋图上应标注截面尺寸和配筋情况，注意按适当比例绘制。梁中纵向钢筋标注方式为根数+钢筋级别符号+直径，如425。

活动1：单筋矩形截面梁正截面设计案例。

【案例2-1】 某建筑物级别为2级的钢筋混凝土矩形截面简支梁，处于室内正常环境，截面尺寸b×h=250mm×650mm，荷载效应组合为基本组合，承受弯矩设计值M=225kN·m，混凝土强度等级为C20，HRB335级钢筋，试配置截面受力钢筋。

解 材料强度设计值fc=9.6N/mm2，fy=300 N/mm2，ξb=0.55；梁处于一类工作环境，取as=40mm；2级建筑物，荷载效应组合为基本组合，K=1.20。

（1）求αs。

（2）求ξ。

截面尺寸满足要求。

（3）求As。

（4）计算ρ。

（5）选配钢筋，绘制配筋图。

查附录A，选配钢筋222+2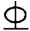25（As=1742mm2）。

dmax=25mm钢筋间距满足要求，正截面配筋图见图2-19。

2.承载力复核

承载力复核是在已知构件截面尺寸、受力钢筋截面面积、混凝土等级和钢筋等级的条件下，验算该正截面承载能力是否满足要求。可按下列步骤进行。

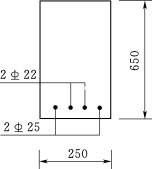
图2-19　正截面配筋图（单位：mm）

第一步：验算配筋率是否满足。若ρ＜ρmin，应重新进行配筋计算。若为已建成的工程，则应降低使用条件。

第二步：按式（2-8）计算相对受压区计算高度ξ，并检查是否满足式（2-9）的条件。若不满足，表示截面属于超筋截面，承载力受混凝土受压区控制，则取ξ=0.85ξb。

第三步：按式（2-6）求αs，即

第四步：计算正截面受弯承载力Mu。

第五步：验算Mu是否满足KM≤Mu。若满足，则截面安全；否则，截面不安全。

活动2：单筋矩形截面梁正截面承载力复核案例。

【案例2-2】 某建筑物级别为3级，其钢筋混凝土矩形截面简支梁的截面尺寸b×h=250mm×500mm，处于室内正常环境，正常使用承受弯矩设计值M=75kN·m，采用混凝土强度等级为C25，HRB335级钢筋，配置受力钢筋为318。试复核该梁正截面受弯承载力是否满足要求。

解 材料强度设计值fc=11.9N/mm2，fy=300N/mm2，ξb=0.55；纵向受拉钢筋截面面积As=763mm2；一类工作环境，as=40mm；3级建筑物，荷载效应组合为基本组合，K=1.20，h0=h-as=500-40-460（mm）。

（1）验算配筋率是否满足要求。

满足最小配筋率要求。

（2）计算相对受压区计算高度ξ。

说明不会发生超筋破坏。

（3）计算系数αs。

（4）计算正截面受弯承载力Mu。

（5）验算正截面承载能力是否满足要求。

正截面承载能力满足要求。