规范化正截面承载力计算

（一）基本假定

钢筋混凝土受弯构件正截面承载力的计算依据的是适筋梁在第Ⅲ阶段末的应力状态。为了建立基本计算公式，《水工混凝土结构设计规范》在大量试验研究的基础上做出以下4条假定。

（1）平截面假定。构件正截面在弯曲变形后仍保持为一平面，即截面上各点的应变之间保持线性变化关系。

（2）不考虑截面受拉区混凝土的抗拉强度，即假定截面受拉区的拉力全部由纵向受拉钢筋来承担。

（3）受压区混凝土的应力-应变关系采用理想化的应力-应变曲线（图2-14）。混凝土弯曲受压时，当εc≤0.002时，应力与应变关系曲线为抛物线；当压应变εc＞0.002时，应力与应变关系曲线为水平线，其极限压应变εcu取0.0033，相应的最大压应力取混凝土轴心抗压强度设计值fc。

（4）软钢的应力与应变关系曲线见图2-15。纵向钢筋的应力等于钢筋应变εc与其弹性模量Eε的乘积，但不应大于其相应的强度设计值。即钢筋屈服之前，应力按σs=Esεs计算；钢筋屈服之后，应力一律取为强度设计值fy。

（二）受压区混凝土的等效应力图形

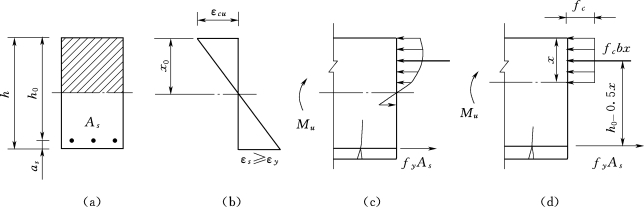
根据平截面假定，可得到每一纵向纤维的应变值，在受压区混凝土的应力与应变关系曲线上可得到与某一应变值对应的应力值。这样，便可绘制出受压区混凝土的应力图形[图2.16（c）]。由于得到的应力图形为二次抛物线，不便计算，根据两个应力图形合力相等和合力作用点位置不变的原则，将其简化为等效矩形分布的应力图形[图2-16（d）]。

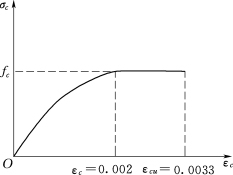
图2-14　混凝土σcεc曲线

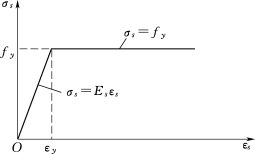
图2-15　有明显屈服点钢筋的应力-应变曲线

(www.xing528.com)

图2-16　单筋矩形截面应力图形转化

（三）相对界限受压区计算高度与受拉纵向钢筋配筋率

1.相对界限受压区计算高度

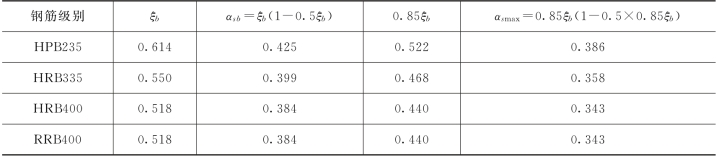
相对受压区计算高度是等效矩形混凝土受压区计算高度x与截面有效高度h0的比值，用ξ=x/h0表示。相对界限受压区计算高度x是指在正截面上受拉钢筋达到屈服的同时，受压区混凝土压应力达到极限压应变，这时混凝土受压区计算高度与截面有效高度h0的比值，称为相对界限受压区计算高度，以ξb表示，即ξb=xb/h0。这一临界破坏状态就是适筋梁与超筋梁的界限。当混凝土强度等级不大于C60时，常用钢筋的ξb值见表2-5。

表2-5　钢筋混凝土构件常用钢筋的ξb、αsb及αsmax值

2.受拉纵筋配筋率ρ

受拉纵筋的配筋率是指受拉钢筋截面面积As与梁截面的有效截面面积bh0的比值，以百分率表示，即

式中　As——纵向受拉钢筋的截面面积，mm2；

　　　b——梁的截面宽度，mm；

　　　h0——梁截面的有效高度，mm。

通常用ρmax表示受拉钢筋的最大配筋率，用ρmin表示受拉钢筋的最小配筋率。当ρ＞ρmax时，说明将发生超筋破坏；当ρ＜ρmin时，说明将发生少筋破坏；当ρmin≤ρ≤ρmax时，说明将发生适筋破坏。为避免发生超筋破坏与少筋破坏，截面设计时，应控制受拉纵筋的配筋率ρ在ρmin～ρmax内。