使用动态客观指标的线性回归模型预测织物热湿舒适性

采用的样本与BP神经网络模型相同（表3－2）。选取4、9、17、21、24、27、31、35号样本的测试数据作为回归模型的预测检验样本，其余样本的测试数据作为多元线性回归模型的建模样本。织物的四项主观评价指标闷热感（Y1）、粘体感（Y2）、潮湿感（Y3）和运动后的冷感（Y4）为因变量，五项静态客观评价指标KTs（X7）、Tequ（X8）、△T（X9）、KTe（X10）和RHequ（X11）为自变量。

采用逐步回归方法，建立闷热感的多元线性回归方程如下：

回归模型的多相关系数为0.992。对回归模型进行方差分析，F＝822.282，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，Tequ和RHequ的p值分别为0和0.007。按α＝0.05水平，回归系数均有显著意义。

采用逐步回归方法，建立粘体感的多元线性回归方程如下：

回归模型的多相关系数为0.949。对回归模型进行方差分析，F＝73.145，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，KTs、Tequ和RHequ的p值均为0。按α＝0.05水平，回归系数均有显著意义。

采用逐步回归方法，建立潮湿感的多元线性回归方程如下：

(www.xing528.com)

回归模型的多相关系数为0.974。对回归模型进行方差分析，F＝147.643，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，KTs、Tequ和RHequ的p值分别为0.011、0.016和0。按α＝0.05水平，回归系数均有显著意义。

采用逐步回归方法，建立运动后的冷感的多元线性回归方程如下：

回归模型的多相关系数为0.988。对回归模型进行方差分析，F＝240.946，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，Tequ、△T、KTe和RHequ的p值均为0。按α＝0.05水平，回归系数均有显著意义。

采用回归方程对8个检验样本进行预测，预测结果如表6－12所示。

表6－12　回归模型预测检验结果

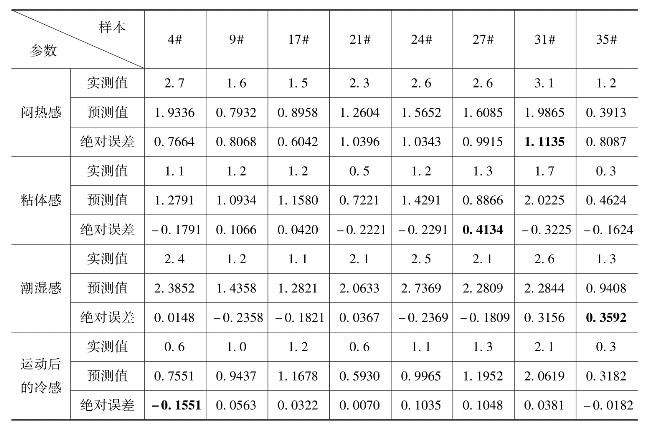
从表6－12可知，回归方程的预测值与实测值有的相差较大，有的很接近。其中闷热感的实测值与预测值的绝对误差最大值为1.1135，平均绝对误差为0.8957；粘体感的实测值与预测值的绝对误差最大值为0.4134，平均绝对误差为0.2097；潮湿感的实测值与预测值的绝对误差最大值为0.3592，平均绝对误差为0.1952；运动后的冷感的实测值与预测值的绝对误差最大值为0.1551，平均绝对误差为0.0644。从回归模型预测结果和网络模型预测结果（对比表6－5）可以看出，除了运动后的冷感外，闷热感、粘体感和潮湿感的多元线性回归模型预测检验结果的平均绝对误差值均比BP网络模型的预测检验结果的平均绝对误差值稍大。相比较而言，BP神经网络预测精度要高，模型的稳定性更好。

再对比以动态客观指标为自变量的织物主观热湿舒适性多元线性回归模型和以静态客观指标为自变量的织物主观热湿舒适性多元线性回归模型，仍然是以动态客观指标为自变量的织物主观热湿舒适性多元线性回归模型的预测精度要高。分析原因仍可能是：相比较6个静态客观指标值，本书中提取的这5个动态特征指标值能更全面地表征人体穿着服装从开始出汗到停止出汗的整个过程的感觉。