基于静态客观指标的织物热湿舒适性线性回归模型

采用的样本与BP神经网络模型相同（表3－2）。选取4、9、17、21、24、27、31、35号样本的测试数据作为回归模型的预测检验样本，其余样本的测试数据作为多元线性回归模型的建模样本。织物的4个主观评价指标闷热感（Y1）、粘体感（Y2）、潮湿感（Y3）和运动后的冷感（Y4）为因变量，6个静态客观评价指标透气率（X1）、透湿率（X2）、芯吸高度（X3）、回潮率（X4）、散湿率（X5）和热阻（X6）为自变量。

采用逐步回归方法，建立闷热感的多元线性回归方程如下：

表6－8～表6－10是采用SPSS软件进行数据处理时，系统给出的结果。

表6－8是多元线性回归模型的概要表。

表6－8　回归模型概要

表6－9显示了模型的方差分析结果，F＝46.211，p＝0。按α＝0.05的水平，认为闷热感与透湿率和热阻之间有线性关系。表中Sum of Squares表示平方和，包括回归平方和和残差平方和。

表6－9　回归模型方差分析

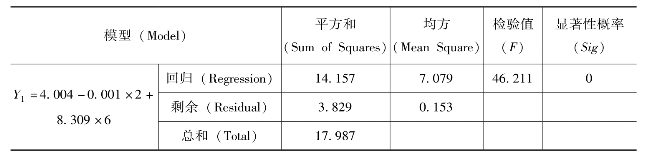
表6－10显示了模型的回归系数检验结果。经t检验，透湿率和热阻的p值均为0，按α＝0.05水平均有显著意义。

表6－10　回归系数检验

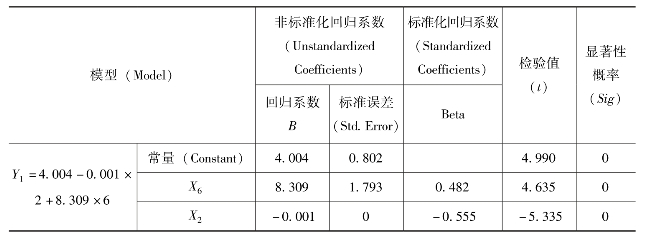
以下模型不再列出相关系数、方差分析和回归系数检验的表格，仅做相关系数、方差分析与回归系数的检验说明。(www.xing528.com)

采用逐步回归方法，建立粘体感的多元线性回归方程如下：

回归模型的多相关系数为0.790。对回归模型进行方差分析，F＝20.716，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，透湿率和热阻的p值均为0。按α＝0.05水平，回归系数均有显著意义。

采用逐步回归方法，建立潮湿感的多元线性回归方程如下：

回归模型的多相关系数为0.743。对回归模型进行方差分析，F＝32.109，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，透湿率的p值为0。按α＝0.05水平，回归系数具有显著意义。

采用逐步回归方法，建立运动后的冷感的多元线性回归方程如下：

回归模型的多相关系数为0.787。对回归模型进行方差分析，F＝42.296，p＝0，按α＝0.05水平，回归方程中的变量之间有线性关系。对模型进行回归系数t检验，散湿率的p值为0。按α＝0.05水平，回归系数具有显著意义。

采用回归方程对8个检验样本进行预测，预测结果如表6－11所示。

表6－11　回归模型预测检验结果

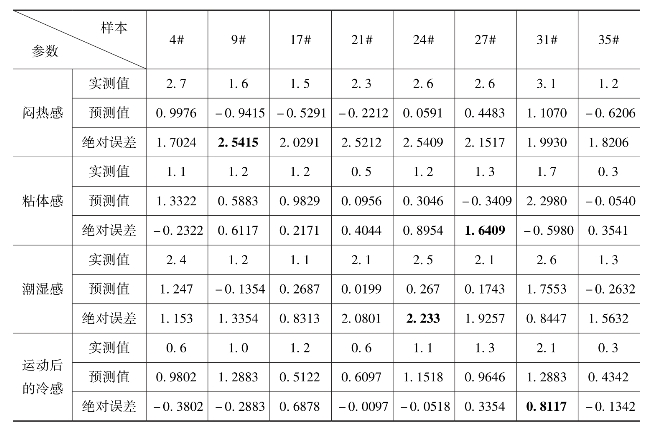
从表6－11可知，回归方程的预测值与实测值相差较远。闷热感的实测值与预测值的绝对误差最大值为2.5415，平均绝对误差为2.1625；粘体感的实测值与预测值的绝对误差最大值为1.6409，平均绝对误差为0.6192；潮湿感的实测值与预测值的绝对误差最大值为2.233，平均绝对误差为1.4958；运动后的冷感的实测值与预测值的绝对误差最大值为0.8117，平均绝对误差为0.3244。从回归模型预测结果和网络模型预测结果（对比表6－3）可以看出，多元线性回归模型的预测检验结果的平均绝对误差值均比BP网络模型的预测检验结果的平均绝对误差值要大。除了粘体感和运动后的冷感的平均绝对误差小于1之外，闷热感和潮湿感的平均绝对误差均超过了1，有的预测值甚至为负值。这些结果说明了闷热感、潮湿感与相关输入指标之间为非线性关系，因此多元线性回归模型不能适用。同时也说明了多元线性回归只能解决线性问题，强行对非线性问题使用线性回归会出现完全不相关的预测值。