基于静态客观指标的织物热湿舒适性预测模型

（一）网络模型的构建

建立模型的主要工作必须合理确定网络的隐层数、网络的输入结点数、隐层的结点数和输出结点数，以及对数据的处理，确定网络的算法和模型参数。

1.输入和输出结点的确定

织物的静态客观评价指标有六个，透气率、透湿率、芯吸高度、回潮率、散湿率和热阻，这六个指标作为输入层参数。织物的主观评价指标有四个，闷热感、粘体感、潮湿感和运动后的冷感，这四个指标作为输出层参数。

2.网络层数的确定

织物的静态客观评价指标和主观评价指标之间不是简单的线性关系，因此对织造建立模型就不能简单地用一层结构，必须采用多层网络。从理论上讲三层BP神经网络可以逼近所有的函数。因此建立的模型都采用三层网络结构，即输入层、输出层和一个隐层。

3.隐层结点数的确定

隐层结点数目的多少对整个网络的性能和预测结果有直接影响。隐层神经元个数参考值可以根据上述的经验公式（6－9）计算。此外还有许多经验公式，不过这些公式大都是依据具体的试验环境而得来的，普遍性不是很好，所以，应结合本书的研究和经验公式得到的参考值，进行试验得出预测模型的最佳隐层结点数。

4.样本数据的预处理和后处理

一般来说，用于BP网络训练的输入样本数据预处理分为两个步骤，即原始数据样本集的标准化与标准化后数据的主成分分析。在BP网络的实际应用中，各指标之间存在着量纲、数量级不同等方面的问题，因此在进行主成分分析之前，需对数据进行标准化。标准化方法可采用零均值标准差标准化方法或者归一化方法，在Matlab中前者由prestd函数来实现，后者由premnmx来实现。实验中发现采用零均值标准差标准化方法比归一化方法效果要好，所以在本书采用prestd函数来实现原始数据样本集数据的标准化。然后采用Matlab函数prepca来实现主成分分析。

由于样本数据在输入BP网络之前已进行了标准化处理，为将输出值还原到原始量纲，应对训练后的网络输出数据进行后处理，对应于数据的预处理过程，在Matlab中用两个函数可完成数据的量纲还原，分别是poststd与postmnmx，为保持前后相对应，本研究采用poststd函数。

（二）网络模型的训练

1.模型网络结构

共采用了36组样本（表3－2），随机挑出4、9、17、21、24、27、31、35号样本的测试数据作为网络模型的预测检验样本，其余样本的测试数据作为网络模型的训练样本，这样随机提取样本的主要目的是为了提高预测的精度。BP神经网络模型的主要程序见附录1，经大量训练，所采用的最佳网络参数见表6－2。

表6－2　BP神经网络预测模型的优化参数

图6－3所示为Trainbr函数训练BP网络的误差变化曲线图。SSE为网络训练误差平方和，SSW为网络权值与阈值平方和，Parameters为有效的权值与阈值个数。这三个参数用来表征Trainbr函数训练过程，Trainbr函数采用贝叶斯规则对SSE与SSW进行最小化，自动获得权值与阈值的有效个数，找到网络的最佳结构，提高网络的泛化能力。在用此函数训练BP网络时，训练结果收敛，网络会给出提示信息“Maximum MU reached”。此外还可以根据SSE和SSW的大小变化情况来判断训练是否收敛，当SSE和SSW的值在经过若干步迭代后处于恒值时，则通常说明网络训练收敛，此时可以停止训练。本模型的迭代至127步SSE和SSW达到恒值，网络收敛，此时网络的有效权值和阈值的个数为48.9029。

图6－3　网络训练过程曲线

2.模型预测结果的对比分析

根据上述网络结构建立了以静态客观指标为输入参数的织物主观热湿舒适性预测模型，并对8个预测检验样本作了预测结果见表6－3。

表6－3　网络模型预测检验结果(www.xing528.com)

从表6－3可知，网络预测值与实测值比较接近。闷热感的实测值与预测值的绝对误差最大值为0.9279，平均绝对误差为0.3441；粘体感的实测值与预测值的绝对误差最大值为1.2519，平均绝对误差为0.4536；潮湿感的实测值与预测值的绝对误差最大值为0.6342，平均绝对误差为0.3001；运动后的冷感的实测值与预测值的绝对误差最大值为0.4129，平均绝对误差为0.2166。除了31号织物的粘体感的实测值与预测值的绝对误差超过1（为1.2519）之外，其他绝对误差值均小于1，平均绝对误差值均小于0.5，这样的预测精度值是在可接受范围内的。

本书采用绝对误差，而非相对误差来分析预测精度，主要是因为4个主观感觉值均采用5级标尺进行评判，评分在0～4之间，每一级标尺相差1分，也就是说只要预测值与实测值的评分相差不到1分，即表示主观穿着感觉非常接近，若采用相对误差来分析预测精度，反而不能很好说明问题。

下面分别以Excel绘图形式来直观的表示8个预测检验样本的各项预测值与实测值的符合情况。图6－4～图6－7分别是闷热感、粘体感、潮湿感和运动后的冷感的预测值与实测值的对比图。

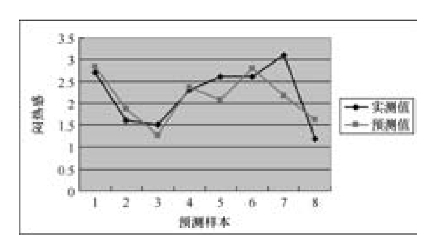
图6－4　闷热感的预测值与实测值的对比图

图6－5　粘体感的预测值与实测值的对比图

图6－6　潮湿感的预测值与实测值的对比图

图6－7　运动后的冷感的预测值与实测值的对比图

为了更好地分析采用该网络模型的预测精度，本书对这8个预测检验样本的实测值与预测值用Origin软件做了相关性分析。图6－8～图6－11分别是闷热感、粘体感、潮湿感和运动后的冷感的预测值与实测值的线性回归图。图中x轴表示实测值，y轴表示预测值，y＝Ax＋B表示相关方程，R为相关系数。从图中可以看出，运动后的冷感的预测值与实测值的相关系数最高，为0.926，也即预测精度最好，粘体感的预测值与实测值的相关系数最低，为0.649，预测精度不太好。闷热感和潮湿感的预测精度居中。

图6－8　闷热感的预测值与实测值的线性回归图

图6－9　粘体感的预测值与实测值的线性回归图

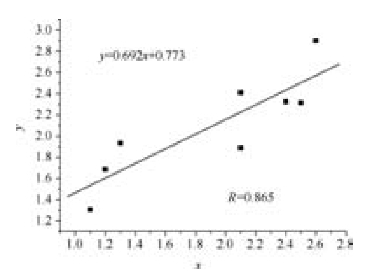
图6－10　潮湿感的预测值与实测值的线性回归图

图6－11　运动后的冷感的预测值与实测值的线性回归图