BP神经网络——结构及算法解析

（一）BP神经网络简介

BP神经网络模型［7］是由输入层、输出层和若干个隐层组成的多层前馈网络模型，误差反向传播（BP）算法是训练前馈网络模型的最常用算法。在BP网络模型中，同层各神经元互不连接，相邻层的神经元通过权值连接。主要用于：

（1）函数逼近：用输入矢量和相应的输出矢量训练一个网络逼近一个函数；

（2）模式识别：用一个特定的输出矢量将它与输入矢量联系起来；

（3）分类：把输入矢量以所定义的合适方式进行分类；

（4）数据压缩：减少输出矢量维数以便于传输和存贮。

（二）BP神经元模型与网络结构

1.BP神经元模型

一个基本的BP神经元模型结构和普通的神经元相同如图6－1所示。不同的是，BP神经元的传递函数f通常取可微的单调递增函数，如对数Sigmoid函数logsig、正切Sigmoid函数tansig和线性函数purelin等。BP网络最后一层神经元的特性决定神经网络的输出特性。当最后一层神经元采用Sigmoid型函数时，整个神经网络的输出被限制在一个较小的范围内；如果最后一个神经元采用purelin型函数，则网络可输出任意值。

2.BP神经网络结构［2］

BP神经网络通常采用基于BP神经元的多层前向神经网络的结构形式。BP神经网络一般具有一个或多个隐层，其中，隐层神经元通常采用Sigmoid型传递函数，而输出层则采用purelin型传递函数。1989年Robert Hecht－Nielson已证明对于任何在闭区间的一个连续函数都可以用具有如图6－2所示结构的BP网络来逼近，因而一个三层结构的BP网络可以完成任意N维到M维的映射［6］，因此，通常BP网络多采用单隐层结构。

图6－2　单隐层BP网络结构

本书亦采用单隐层的BP神经网络建模。在三层前馈网络模型中，输入向量X＝（x1，x2，…，xi，…，xn）T，如加入x0＝－1，可为隐层神经元引入阈值；隐层输出向量为Y＝（y1，y2，…，yj，…，ym）T，如加入y0＝－1，可为输出层神经元引入阈值；输出层向量为O＝（o1，o2，…，ok，…，ol）T；期望输出向量为D＝（d1，d2，…，dk，…，dl）T。输入层到隐层之间的权值矩阵用V表示，V＝（V1，V2，…，Vj，…Vm），其中列向量Vj为隐层第j个神经元对应的权向量；隐层到输出层之间的权值矩阵用W表示，W＝（W1，W2，…，Wk，…，Wl），其中列向量Wk为输出层第k个神经元对应的权向量。由此得到各层之间的数学关系：

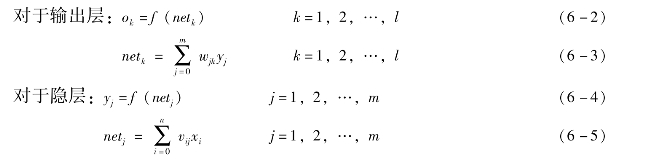
6－2与6－4两式中的f（x）为转移函数，隐层神经元一般采用单极性的对数Sigmoid函数：

该函数具有连续、可导的特点；输出层神经元采用纯线性变换函数。

（三）BP神经网络的学习算法

BP（Back—Propagation）神经网络是一种前馈式、反向传播学习算法的人工神经网络。BP神经网络的工作原理是将数据输入网络输入层，输入层单元接收输入信号，经传递函数向前传播到隐含层节点，计算权重，再把隐层节点的输出信号传播到输出节点，最后给出输出结果。

1.一般的BP算法

BP算法学习过程的主要所在是反向传播，即当输出值与目标值产生误差时，反向传播修正各权重值以达到最小误差。具体算法为：

（1）给初始权值、阈值、目标值和输入值x，计算实际输出y：

（2）检验yj与的差异并与期望误差E对比看是否满足，或看E是否最小，如满足则结束。

（3）反馈修正权值：沿网络通路反向传播，通过修正各权值，使误差最小；(www.xing528.com)

其中ωij为连接点第i和j层间的权值，η为步长大小，t为权值修正次数，α为动量因子，δpj为j节点p模式的局部误差，由目标输出与系统输出yj的差值直接求得。

（4）达到了期望误差E或最小后停止学习输出yj，否则返回第二步。

2.BP算法的改进

在实际应用中，原始的BP算法很难胜任，因此出现了很多改进算法。BP算法的改进主要有两种途径，一种是采用启发式学习方法；另一种则是采用更有效的优化算法。

现在的神经网络中主要采用动量法和学习率自适应调整两种策略，从而提高了学习速度并增加了算法的可靠性。动量法降低了网络对于误差曲面局部细节的敏感性，有效地抑制网络陷于局部最小；自适应调整学习率有利于缩短学习时间。本书准备采用改进的BP算法训练神经网络模型，对于不同的预报对象有可能采取不同的BP改进算法。

（四）BP神经网络模型的构建、训练和仿真［3］

本书采用MATLAB神经网络工具箱函数编程，来实现对BP网络模型的构建、训练与仿真。

1.网络模型的构建与初始化

构建BP网络模型的第一步是建立网络对象并初始化，可用MATLAB神经网络工具箱函数newff来建立一个可训练的单隐层BP网络，其语法为：

net＝newff（PR，［S1 S2］，｛TF1 TF2｝，BTF，BLF，PF）

这里，PR是一个R×2的矩阵，以定义R个输入向量的最小值和最大值；｛TF1 TF2｝是包含每层用到的转移函数名称的细胞数组，本书取TF1为tansig，其函数表达式见式（6－6），它的作用是将神经元的输入范围（－∞，＋∞）映射到（0，＋1），TF2为purelin，为纯线性变换函数，其输出范围为（－∞，＋∞）；BTF是用到的训练函数的名称，本书主要采用trainbr函数；BLF为权值与阈值的学习函数，本书采用learngdm，其为带动量项的BP学习规则；PF为网络运行性能表征方式，本书采用最小误差平方和函数mse。［S1 S2］是一个包含每层神经元个数的数组，本书的BP网络输出节点为4个，因此，S2＝4，S1根据具体情况来取得，有经验公式可以利用［8］：

式中m为输入层节点数，n为输出层节点数，S1为隐层节点数。

对前馈网络来说，有两种不同的初始化方式经常被用到：initwb和initnw。initwb函数根据每一层自己的初始化参数（net.inputWeights｛i，j｝.initFcn）初始化权值矩阵和阈值。前馈网络的初始化权值通常设为rands，它使权值在－1到1之间随机取值，这种方式经常用在转移函数是线性函数时。initnw通常用于转移函数是曲线函数时，它根据Nguyen和Widrow规则为各层产生初始权值和阈值，使得每层神经元的活动区域能大致平坦地分布在输入空间。它比起单纯地给权值和阈值随机赋值有以下优点：（1）减少神经元的浪费（因为所有神经元的活动区域都在输入空间内）；（2）有更快的训练速度（因为输入空间的每个区域都在活动的神经元范围中）。本书采用newff函数调用initnw方式，建立网络对象并且初始化网络权值和阈值，此后，网络模型就可以进行训练了。

2.网络模型的训练

在MATLAB神经网络工具箱中有很多训练BP网络的函数，如traingd，traingdm，traingda，traingdx，trainlm，trainbr等，分别对应于不同的改进BP算法。本书主要采用trainbr函数。在使用trainbr函数对BP网络进行训练之前，先要对其参数进行赋值，一般有如下参数需赋值（表6－1），其他参数可取缺省值。

表6－1　trainbr训练函数内部参数

然后调用函数train进行训练，并将训练后的网络结构保存在net数组中，语法为：

net＝train（net，Pd，T1）

网络在训练的过程中，将根据程序显示训练前的权重值和阈值，以及训练后的权重值和阈值，绘制出比例图，该过程可以用hintonwb函数实现。

3.网络模型的仿真

BP网络每一次训练结束后，都进行网络性能的验证。验证时，使用sim函数模拟训练后的网络，其接收新的网络输入pnew，网络对象net，返回网络输出anew，其语法为：

［anew］＝sim（net，pnew）

可以通过预报误差分析或者相关性分析来验证网络预报精度，看能否作为准确的预报工具。