算法设计优化与刀路轨迹设计

10.3.3.1算法设计</ID=5>

1）实例10-2车削凹椭圆，采用的思路是用X值作为变化的步距，根据椭圆方程来计算Z值，在椭圆方程中心的右边，X值是逐渐增加的，而在椭圆方程中心的左边，X值是逐渐减小的。

2）根据椭圆的参数方程建立图10-8所示的数学模型。

由数学知识可知椭圆参数方程表达式：X=Asinθ和Z=Bcosθ，tanθ=A/B，其中公共参数设为角度量θ。结合数学模型图，设置#100号变量控制椭圆的角度变化，由椭圆参数方程可知：任意角度对应的数学表达式为#101=19*SIN[#100]、#102=30*COS[#100]。

由加工零件图以及数学知识并结合图10-8数学模型图可知，实例10-2凹椭圆的起始角度#100=0、终止角度#100=180。

3）采用拟合法（无限逼近椭圆轮廓）车削椭圆轮廓，设置#100号变量控制角度变化利用椭圆的参数方程，计算出角度对应的X、Z的值，X、Z的值构成了一个点的坐标（位置）。通过角度的变化引起点的变化，随着角度按照一定的规律变化，从而引起点的变化这些点的运动轨迹构成凹椭圆轮廓。规划的刀路轨迹如图10-9所示。

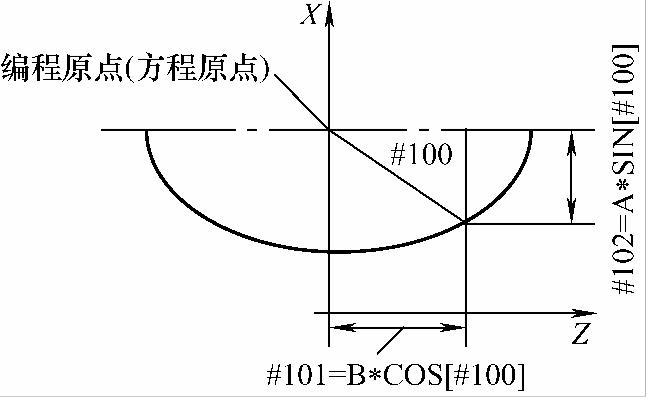
图10-8 凹椭圆数学模型示意图

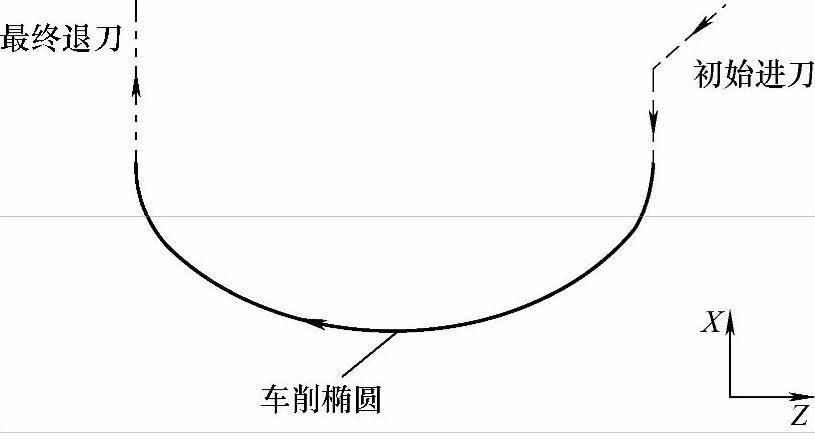
图10-9 车削凹椭圆刀路轨迹规划图

4）同心椭圆法车削凹椭圆弧。

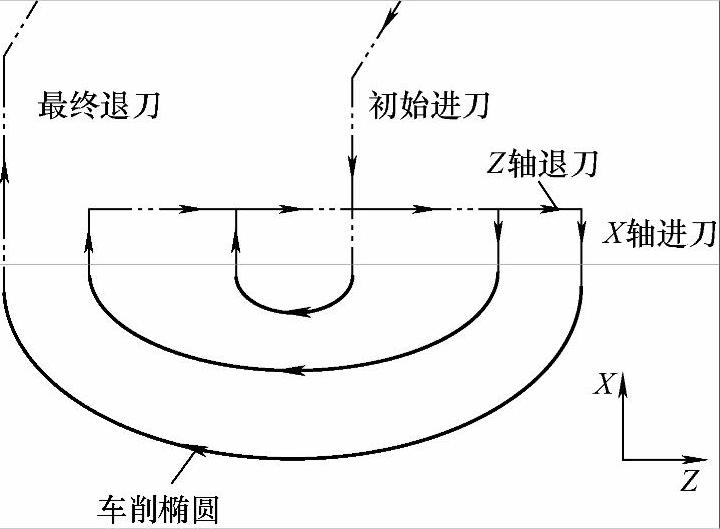
同心椭圆法编程思路：先车削一个长、短半轴较小（如R3mm）的凹椭圆弧，车削一次后X、Z轴退刀至下一次车削凹椭圆弧加工的起点，准备下一次车削凹椭圆弧，下一次车削椭圆弧的长、短半轴要比上一次车削椭圆弧的长、短半轴要大（车削凹椭圆弧长、短半轴按照一定的规律逐渐增大至零件尺寸），直至凹椭圆弧加工结束。规划的刀路轨迹如图10-10所示。

同心椭圆法车削凹椭圆弧的步骤如下：

1）设置#113=3、#111=1.9控制起始加工凹椭圆弧长、短半轴的值。

2）X、Z向进刀至凹椭圆圆弧加工起点，车削椭圆长、短半轴值为：#113=3、#114=1.9凹椭圆弧。

3）通过条件判断语句IF[#100 LT 10]GOTO 10判断凹椭圆弧是否车削完毕，如车削完毕，X、Z轴退刀，加工结束；如凹圆弧没有车削完毕，则执行步骤4）。

4）X、Z向进刀至下一次车削长短半轴值为：#113=#100+3、#111=#111+1.9凹椭圆弧的加工起点位置，准备进行下一次车削凹椭圆。

5）循环执行1）～4）操作步骤直至凹椭圆弧车削完成，程序设计流程如图10-11所示

(www.xing528.com)

图10-10 “同心椭圆法车削凹椭圆”刀路轨迹规划图

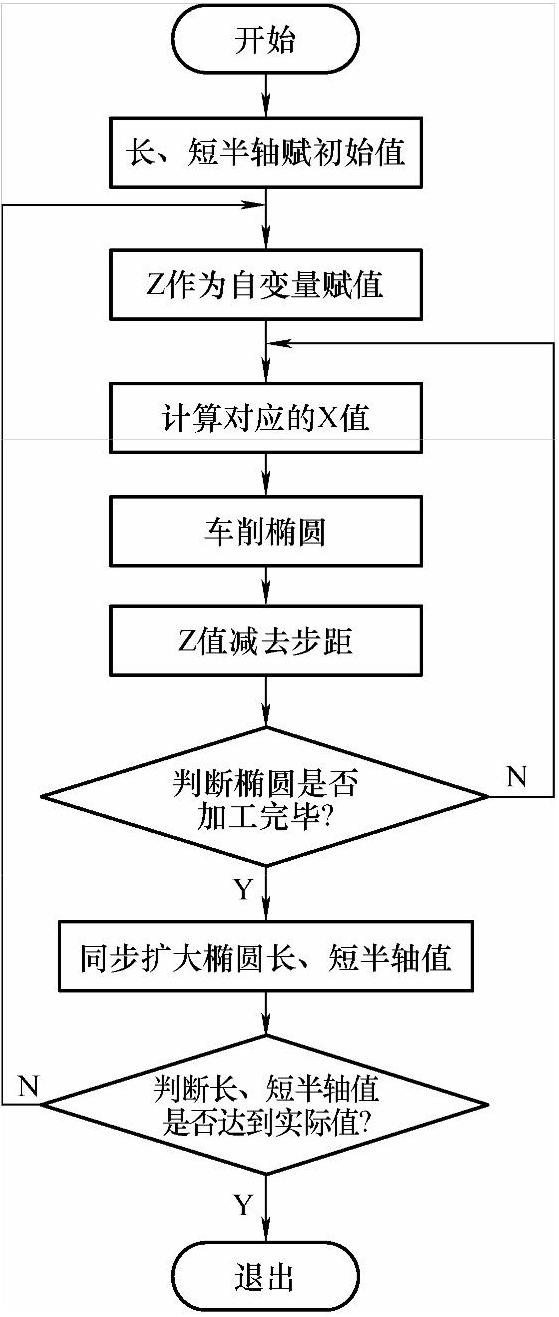
图10-11 “同心椭圆法车削凹椭圆”程序设计流程框图

10.3.3.2根据算法以及流程框图编写加工的宏程序代码</ID=6>

1.根据椭圆参数方程编写凹椭圆精车轮廓宏程序加工代码</ID=7>

编程要点提示</ID=2>

1）程序O1006车削凹椭圆轮廓的精加工程序，只能应用于已经去除大量余量的精加工轮廓，否则会产生扎刀。

2）由于是整体凹椭圆轮廓，因此程序中X值应该设置为#104=60-#103。

3）设置语句#107=#101-50，是因为椭圆中心和编程原点不是同一个点，相距50mm

2.采用同心椭圆法编制宏程序代码</ID=4>

编程要点提示</ID=2>

1）本程序采用同心椭圆方法车削凹椭圆轮廓的程序，也包含粗加工程序。该程序采用“分割曲线轮廓”和“直线逼近曲线轮廓”的编程思路，大概为：先把椭圆长、短半轴分为均匀的10等份，先车削一个小椭圆轮廓，然后逐渐增加椭圆的长、短半轴值，慢慢逼近最终椭圆的轮廓。

2）每次车削凹椭圆轮廓长、短半轴的尺寸都不一样，语句G0 Z[#101-50]是控制每次Z向的进刀点。