金属表面的扩散机制与缺陷相关性分析

扩散是指原子、离子或分子因热运动而发生的迁移。固体的扩散是通过固体中原子、离子或分子的相对位移来实现的。原子在多晶体中的扩散可按体扩散（晶格扩散）、表面扩散、晶界扩散和位错扩散四种不同的途径进行。其中表面扩散，即原子在晶体表面的迁移，所需的扩散激活能最低。许多金属的表面扩散所需的热能为62.7～209.4kJ·mol^-1。随着温度的升高，越来越多的表面原子可以得到足够的激活能得以与近邻原子的键断裂而沿表面运动。固体表面的任何原子或分子要从一个位置移到另一个位置，也必须像晶体点阵内一样，克服一定的势垒，即扩散激活能，而且要到达的位置必须是空着的，这就要求点阵中有空位或其他缺陷。缺陷构成了扩散的主要机制。但是，表面缺陷与晶体内部的缺陷有一定的差异，因而表面扩散与体扩散也不相同。

1.表面缺陷及其能量

（1）表面缺陷 单晶表面的TLK模型（图1-2）说明晶体表面存在着低晶面指数平台、单分子或单分子高度的台阶和扭折。表面缺陷中由热激发所引起的表面空位、表面增原子和表面杂质原子等容易发生在TLK结构的表面上。

表面空位指在一维点阵的格点上失去原子所形成的空位缺陷。它除了经常出现在TLK结构的表面上外，也可出现在一般重构表面上。在热激发下，某些表面原子有可能脱离格点而进入晶体内部成为增原子，并在表面留下空位；或者某些表面原子脱离格点挥发以及在表面迁移，形成空位。

表面增原子指二维点阵以外出现的额外同质原子。其位置可在TLK结构的平台、台阶和扭折处。在热激发下，某些晶体内部的位移原子可能连续不断地迁移而最后定位在表面处，成为表面增原子，而在晶体内部留下空位，这种缺陷称为肖特基（Schottky）缺陷。表面增原子也可以通过表面原子的迁移而形成。

表面杂质原子是指杂质原子占据表面的一些晶格格点或间隙位置后形成的缺陷。吸附、晶体内部向表面扩散杂质、合金化等，都是这种缺陷的来源。

碱卤化合物等离子晶体表面在辐射、渗入杂质或过量成分、电解等条件下，常由于正负离子缺位，或电子进入表面而形成荷电中心，这类缺陷称为色心和极化子。色心根据形成机理大致可分为俘获电子心、俘获空穴心和化学缺陷心等。目前研究最多的色心是碱卤化合物中的F心，它是一个负离子空位俘获一个电子所构成的系统。其他重要的色心还有正离子空位俘获空穴形成的V心（及V_k心）以及复合结构的H心、M心、R心等。极化子是指电子进入离子晶体表面所造成的点阵畸变。当电子进入晶格后，其附近的正离子被吸引，负离子被排斥，产生离子位移极化，其构成的库仑场反过来又成为束缚电子的“陷阱”。一个自陷态电子和晶格的极化畸变，形成了一个准粒子称为极化子。换言之，进入离子晶体的电子与周围极化场构成的总体称为极化子。

（2）表面缺陷的能量和熵 严格计算表面缺陷的能量和熵，需要采用量子力学的方法，这较为复杂。通常采用经典的近似方法，假设固体中原子之间存在成对作用，按表面原子之间的结合势来计算表面缺陷形成能和迁移能。空位缺陷的形成能为

式中 ΔE_T——从平台上移动一个原子离开平台点阵所需的能量；

ΔE_K——该移动原子落入另一格点（扭折或台阶边缘）时所消耗的能量；

ΔE^v_R——平台失去一个原子后平台空位周围点阵弛豫畸变所消耗的能量。

表面增原子的形成能为

式中 ΔE_K——原子脱离格点（多在TLK结构的扭折处）所需的能量；

ΔE_A——原子占据台阶格点所消耗的能量；

ΔE^a_R——平台或台阶吸附一个增原子而引起点阵畸变所消耗的表面弛豫能。

以上各项能量与表面原子之间的结合势有关。Wynblatt和Gjostein利用莫尔斯势对Cu、W等进行了计算。莫尔斯为计算金属表面能提出的势能函数为

式中 D、a——两个调节参数。

Wynblatt等将其修正为

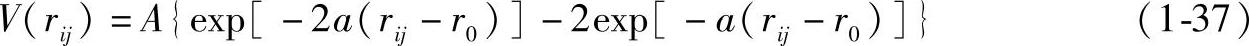
式中 a、r₀、A——常数；

r_ij——两原子i和j之间的距离。

表1-3为对铜晶体计算的结果。

表1-3 铜晶体表面缺陷形成能和迁移能

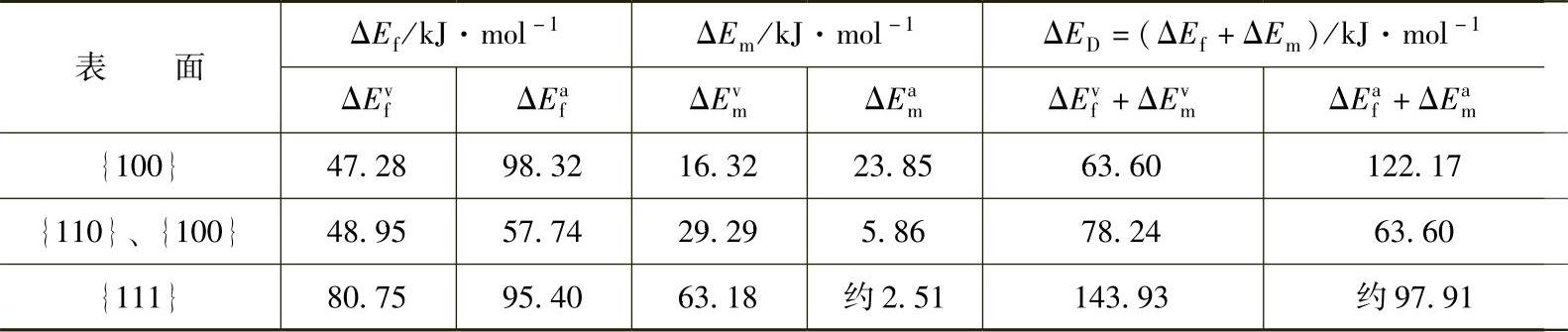
从表1-3中可以看出，在原子密排面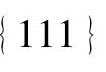处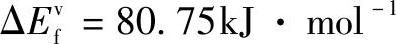，，95.40kJ·mol^-1，而铜晶体结合能为336.39kJ·mol^-1，约为表面缺陷形成能的4倍。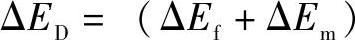，其中，ΔE_D为跃进激活能；ΔE_f为表面缺陷形成能；ΔE_m表示表面缺陷迁移能，即表面原子或表面空位由一个平衡位置越过势垒跃迁到邻近格点位置时所需的能量，其数值上等于原子互作用势垒的高度。

同样，Wynblatt等对表面缺陷迁移能作了计算（表1-3）。假定唯一的扩散物质是吸附原子，它表示一个吸附原子从一个平衡位置到另一个平衡位置伴随扩散跳跃的能量变化。由于缺陷在迁移前、后或过程中，正常格点的弛豫都要受到周围格点弛豫的影响，所以缺陷的迁移能实际上包含了原子能势垒和势谷时的弛豫能。图1-14中的实线表示扩散跳跃时真正的能量变化，虚线表示原子在跳跃过程中周围格点的弛豫能，ΔE₂为弛豫势垒高度，ΔE₁为势谷弛豫能，ΔE₃为势垒（鞍点）弛豫能，则表面缺陷迁移能为

由玻耳兹曼关系式S＝klnW，可以写出表面缺陷所引起的熵增。例如，由表面增原子引起的熵增（组态熵），即表面缺陷形成熵为

式中 W₀——表面未出现缺陷时的平衡态热力学概率；

W_f——表面出现缺陷时的非完整表面态热力学概率；

k——玻耳兹曼常数。

W₀和W_f可以用原子振动频率来计算，从而可计算出ΔS _f。同样，也可以计算得到表面缺陷迁移熵。

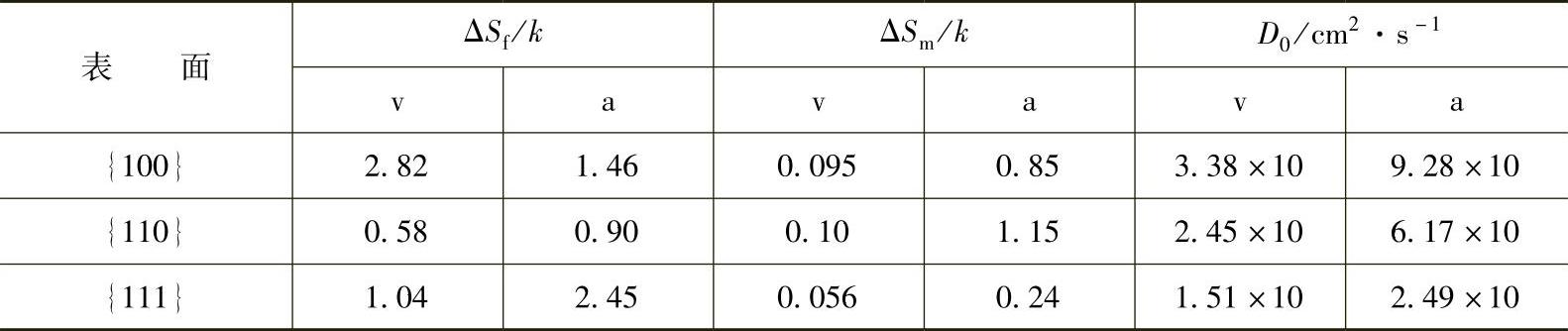
温布拉特（Wynblatt）等计算的铜晶体的ΔS_f和ΔS_m见表1-4。表中v表示表面空位，a表示表面增原子，ΔS_f为形成熵，ΔS_m为迁移熵，D₀为频率因子，定义为

式中 a——常数；

v——频率；

l——缺陷迁移的平均自由程。

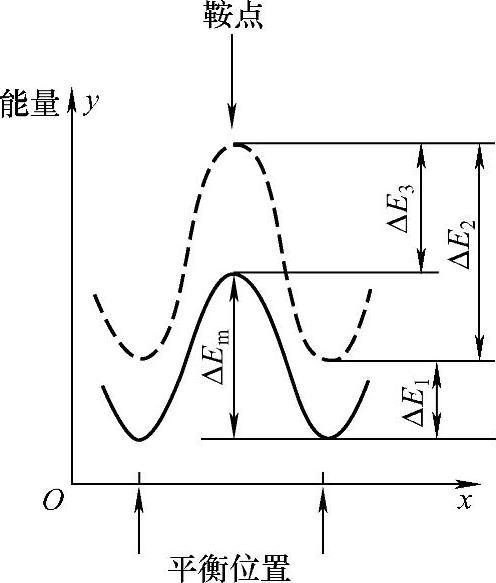
图1-14 缺陷迁移时各能量项示意图

表1-4 铜晶体表面缺陷形成熵与迁移熵

2.表面扩散系数

扩散是物质中原子、离子或分子的迁移现象，是物质传输的一种方式。在气体及液体中，物质传输一般是通过对流和扩散进行的。在固体中不存在对流，扩散成为传输的唯一方式。扩散问题可以从两方面进行分析：一是根据测量的参数描述质量传输的速率和数量，研究扩散现象的宏观规律，可以称为扩散的唯象理论；二是扩散的微观机制，把一个原子的扩散系数与它在固体中的跳动特性联系起来，这是扩散的原子理论。

表面扩散与体内扩散一样，也有自扩散和互扩散两种情况，前者是基质原子在表面的扩散过程，后者是外来原子沿表面的扩散。表面原子的自扩散机制与晶体体内基本相同，但存在两个区别：一是表面原子有更大的自由度，并且扩散激活能远小于体内，因而扩散速率远大于体内；二是表面扩散机制可能因不同晶面而异，例如，面心立方{100}晶面的表面扩散主要为表面空位机制，而{110}晶面主要为增原子扩散机制。

如前所述，TLK模型是单晶表面结构的基本模型。TLK表面的势能是一个复杂的三维函数。表面原子沿这种表面扩散，不可能保持均匀单一速率。为简化计算程序，假设表面原子以平均长度l作无序跳动，连续两次跳动之间的平均时间为τ，根据无序跳动理论，扩散系数的一般表达式为

式中 a——与晶体结构和缺陷运动状况有关的常数。对于简单立方晶系，一维运动取(www.xing528.com)

a＝1/2，表面二维运动取a＝1/4，体内三维运动取a＝1/6。

又设p为单位时间内原子跳动的次数，称为跳动概率，即

由统计理论可得

式中v₀——表面原子的本征频率；

ΔE_D——跳动激活能，它是缺陷形成能ΔE_f与迁移能ΔE_m之和，即

这样，可得表面自扩散系数表达式

如果考虑到原子周围缺陷的形成概率p_f和迁移概率p_m，则表面自扩散系数应表达为

令，则

式中 D₀——与温度无关的频率因子。

由于表面缺陷的形成和迁移都使系统的熵增加，以及

因而

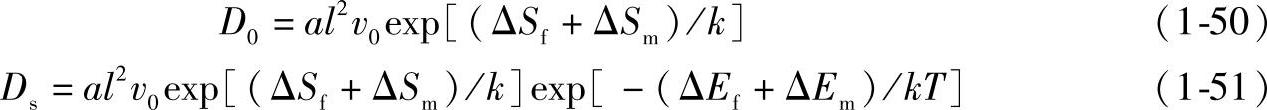
上述表面自扩散是原子跳动的长度与点阵原子间距具有相同数量级的情况，属于短程扩散，可称为局域扩散。如果温度升高，表面原子能量随之增加，可以处于较高的激发态，其跳动的长度会比点阵原子间距长得多，即属于长程扩散，称为非局域扩散。为了说明这个概念，可参考图1-15所示的体心立方（100）表面吸附原子运动的例子。

对于（100）表面上的吸附原子，由于声子的相互作用（热起伏现象），在某一时刻可从平衡位置越过一个鞍点，鞍点位置的能量为迁移能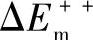，扩散跳跃长度与点阵原子间距同数量级。如果原子积累的能量比表面扩散最小能量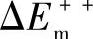大得多（隧道效应除外），它就有能力沿图中箭头3跳到远处，此时跳跃路径比点阵原子间距长得多，若以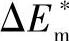表示完成这种跳跃的最小能量，并以ΔE_s表示平台吸附原子的束缚能，则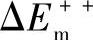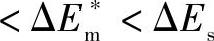。当然它可能沿箭头2所示的路径扩散到次邻近A、B位置。把图1-15a中1、2所示的短程扩散称为局域扩散，而把3所示的长程扩散称为非局域扩散。

图1-15b是吸附原子作局域扩散、非局域扩散以及处于蒸发态下的能量范围。每种状态各有不同的自由度分配。例如，局域扩散原子具有两个振动自由度和一个平移自由度；在非局域扩散状态下则具有两个平移自由度和一个振动自由度。大分子物质的扩散具有更复杂的自由度分配。由以上分析可见，表面扩散时原子可能跳跃到固体表面上的三维空隙位置后进入另一个新位置，此时能量只要大于ΔE_m^*，而小于ΔE_s。体扩散不可能出现这种情况，它不存在这种附加自由度。

表面互扩散（异质扩散）是外来原子沿表面的扩散。外来原子在表面以间隙、置换、化合、吸附等方式存在，由于受势场束缚较弱，其跳动速率远大于自扩散。如果外来原子是置换式的，那么在点阵弛豫作用下，表面缺陷的形成和迁移概率增大，从而使扩散系数增大；如果外来原子是间隙式的，那么它们的迁移仅与表面势垒有关，扩散系数表示式（1-47）中的ΔE_D仅有ΔE_m一项，此时v₀为外来原子的振动频率。

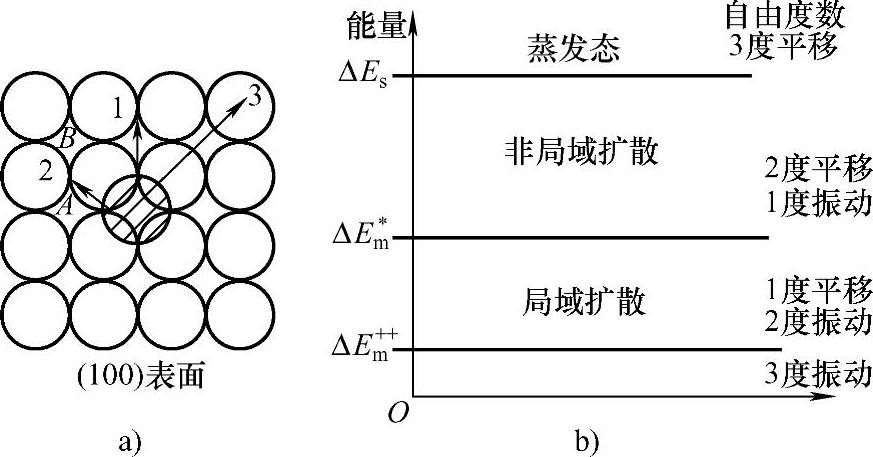
图1-15 体心立方（100）表面吸附原子的运动及其激活能

a）吸附原子的平衡位置及可能跃迁途径 b）吸附原子局域扩散、非局域扩散以及蒸发态下的能量图

3.表面扩散的试验研究和唯象理论

表面扩散的主要特征表现于表面扩散系数，现有许多测定表面扩散系数的方法。

（1）示踪法 它可用来求出不同杂质的表面扩散系数和激活能。这是一种较为古老的方法，由于蒸发和体扩散，示踪物质容易流失。

（2）传质法 传质法是用光学方法观察表面扩散传质引起的表面形貌变化，进而计算出表面扩散系数和激活能的一种方法。用于试验研究的传质法有晶界沟槽化、单划痕衰减、划痕衰减（正弦轮廓）、小面化、烧结、晶界孔洞生长、钝化等。主要测量手段及方法有干涉显微镜、激光衍射轮廓和场发射成像。试验时要设法减少表面污染的影响。

（3）场离子发射显微镜法（FIM）和场电子发射显微镜法（FEM）它们通常是观察吸附原子在难熔金属制成的场发射尖端表面上的位移，进而测量异质表面扩散系数和激活能。

下坡扩散是指从浓度高处向浓度低处扩散。在自然界中，也可由于某种原因出现从浓度低处向浓度高处扩散的现象，也就是形成上坡扩散。因此，真正的扩散驱动力并不是浓度梯度，而应该是化学势的变化∂μ/∂x。在多组元系统中，组元i的化学势可看成每个i组元原子的自由能，而化学势对距离求导就是原子所受的化学力F_c，即扩散驱动力（F_c）i＝-∂μ/∂x，其中负号表示扩散总是沿化学势减小的方向进行。至于引起扩散的具体原因，要作具体分析。对表面扩散来说，大致有以下两个重要类型：

1）由浓度梯度引起的表面扩散。处理这类表面扩散问题的步骤与体扩散类似。如果已知扩散系数，那么可用菲克（Fick）第一定律或第二定律根据边界条件求解，以此计算出由浓度梯度引起的表面扩散通量或各区域浓度随时间的变化值等。

2）由毛细管作用力引起的表面扩散。这类扩散是由表面自由能最小化引起的，属于这类表面扩散的有许多。例如，为使表面自由能与晶界能达到平衡而在晶界附近原来平坦抛光的表面上形成晶界沟（槽）的表面扩散；人为造成周期性（正弦）表面原子密度分布引起表面平坦化的表面扩散；非周期性表面原子密度分布引起表面痕迹衰变的表面扩散；与线性小面横向生长（即在一定的条件下原先是平坦的表面会出现不同于邻位表面取向的独立小面）有关的表面扩散；在高温下粒子靠吸附原子从高化学势到低化学势而实现聚集的表面扩散；在场电子发射显微镜中触针由尖变钝的表面扩散。

上述各种表面扩散原子的化学势μ（x）通常可用Gibbs-Thomson公式表示为

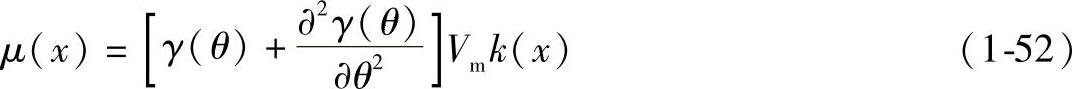
式中 γ（θ）——表面自由能，与表面的结晶取向有关；

V_m——摩尔体积；

k（x）——与表面形状有关的主曲率函数。

且

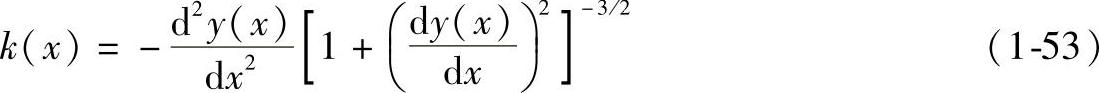
式中 y（x）——描述表面原子分布的函数。

如果表面扩散只在结晶取向的小范围内进行，γ（θ）和γ″（θ）用平均值γ₀和γ₀″代替，那么扩散流通量为

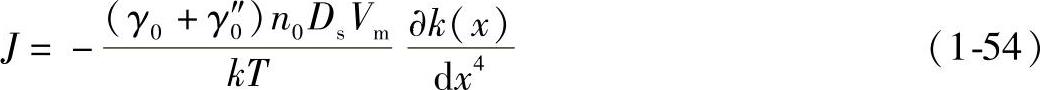
式中 n₀——单位面积的原子位置总数目；

D_s——表面扩散系数。

扩散流引起表面原子密度分布改变，y（x）的变化速率为

利用适当的边界条件，可对式（1-54）求解。