固体表面吸附现象及比表面积测定方法

表面现象一般是指具有确切表面的固体、液体表面上产生的各种物理化学现象，如吸附、润湿等现象都是表面现象。表面现象在金属表面技术中具有重要的作用。表面现象与表面自由能有密切关系，因此与表面自由能一样，表面现象普遍存在于多相体系中。表面和界面吸附和润湿是两种重要的表面现象。

1.气体在固体表面上的吸附

固体表面的吸附作用是表面自由能存在所引起的一种普遍存在的现象。固体不能像液体那样改变表面形状、缩小表面积、降低表面自由能，但可利用表面分子的剩余力场来捕捉气相或液相中的分子，降低表面自由能以达到相对稳定状态。吸附作用使固体表面自由能降低，是自发过程，因而难以获得者真正清洁的固体表面。

气体物质在固体表面上浓集的现象称为气体在固体表面上的吸附。被吸附的物质称为吸附质，具有吸附能力的固体称为吸附剂。常用的吸附剂有硅胶、分子筛、活性炭等。为了测定固体的比表面积，常用的吸附质有氮气、水蒸气、苯或环己烷的蒸气等。

2.物理吸附与化学吸附

吸附是固体表面质点和气体分子相互作用的一种现象。按作用力的性质可分为物理吸附和化学吸附两种类型。物理吸附通过分子间力（范德华力）实现，它相当于气体分子在固体表面上的凝聚。化学吸附实质上是一种化学反应。因此这两种吸附在许多性质上都有明显的差别。

（1）物理吸附 具有如下特点的吸附称为物理吸附：

1）吸附力是由固体和气体分子之间的范德华引力产生的，一般比较弱。

2）吸附热较小，接近于气体的液化热，一般在每摩尔几千焦以下。

3）吸附稳定性不高，吸附与解吸速率都很快。

4）吸附无选择性，任何固体可以吸附任何气体，当然吸附量会有所不同。

5）吸附可以是单分子层的，也可以是多分子层的。

6）吸附不需要活化能，吸附速率并不因温度的升高而变快。

物理吸附仅是一种物理作用，没有电子转移，没有化学键的生成与破坏，也没有原子重排等。

图1-7中pp′是H₂在金属镍表面发生物理吸附过程的势能曲线，其可由量子力学计算出来。当H₂远离Ni表面时，势能为零；当H₂逐渐接近Ni表面时，范德华引力起主要作用，势能逐渐降低；吸附平衡时（到达a点），势能最低，形成了物理吸附的稳定状态。在曲线最低点a处，放出的能量相当于物理吸附热Q_p。而相应的距离r_a相当于表面Ni原子和H₂分子的范德华半径之和（约0.32nm）。但分子进一步接近时，由于电子云重叠引起相斥作用而使势能迅速上升。

（2）化学吸附 具有如下特点的吸附称为化学吸附：

1）吸附力是吸附剂与吸附质分子之间产生的化学键力，一般较强。

2）吸附热较高，接近于化学反应热，一般在40kJ·mol^-1以上。

3）吸附很稳定，一旦吸附，就不易解吸。

4）吸附有选择性，固体表面的活性位只吸附与之可发生反应的气体分子，如酸位吸附碱性分子，反之亦然。

5）吸附是单分子层的。

6）吸附需要活化能，温度升高吸附和解吸速率加快。

化学吸附相当于吸附剂表面分子与吸附质分子发生了化学反应，在红外、紫外-可见光谱中会出现新的特征吸收带。图1-7中cc＇是H₂在金属镍表面发生化学吸附过程的势能曲线。在相互作用的势能曲线上，H₂分子获得解离能D_H-H，解离成H原子，处于c＇的位置。曲线cc＇是解离状态的H原子在固体Ni表面上发生化学吸附时势能E与Ni和H原子距离之间的关系。随着H原子向Ni表面靠近，势能不断下降，达到b点，这是化学吸附的稳定状态。Ni和H原子之间的距离等于两者的原子半径之和。能量E_b是放出的化学吸附热Q_c，这相当于两者之间形成化学键的键能。随着H原子进一步向Ni表面靠近，由于核间斥力，位能沿bc线迅速上升。

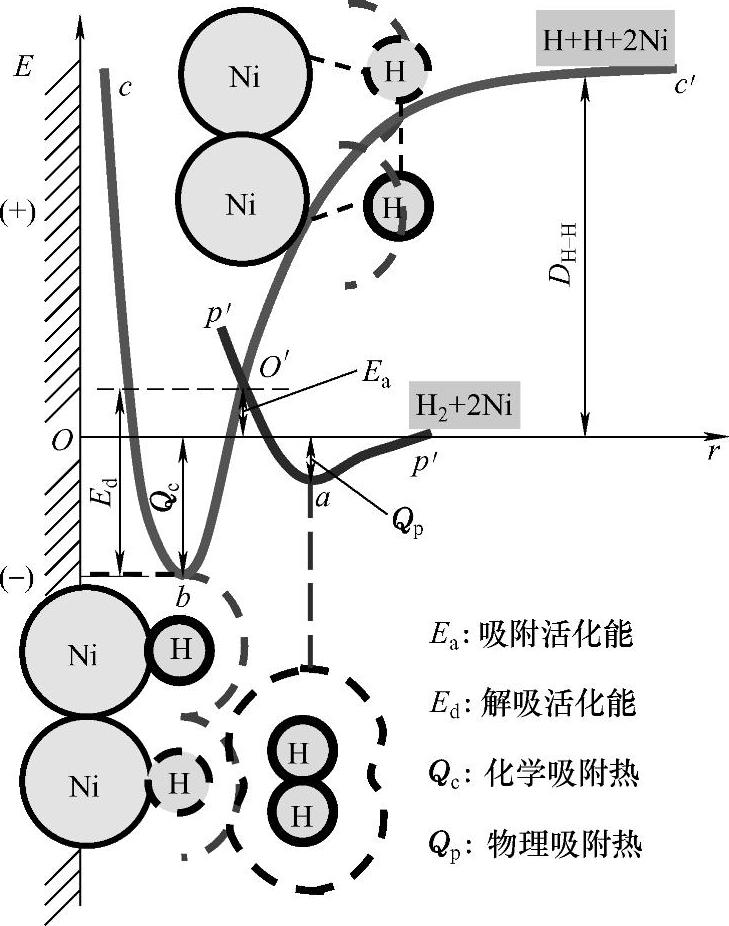
图1-7 H₂在金属镍表面发生物理吸附和化学吸附

3.吸附热力学

（1）吸附热 如前所述，在给定的温度和压力下，吸附都是自发进行的，所以吸附过程的表面自由能变化ΔG＜0。而且气体分子被吸附在固体表面上时，气体分子由原来在三维空间中运动，转变为在二维空间上运动，混乱程度降低，因而过程的熵变ΔS＜0。根据热力学公式

ΔG＝ΔH-TΔS

必然吸附热ΔH＜0，即等温吸附过程是放热过程。大多数试验结果也证实了气体在固体上的吸附是放热的（H₂在Cu、Ag、Au和Cd上的吸附是吸热的，这与它们的化学吸附性质有关）。

吸附热的大小是直接反映吸附剂和吸附质分子之间的结合力强弱和吸附性质的重要参数。吸附热大说明吸附键强，反之说明吸附键弱。吸附热小，与气体的液化热接近，为物理过程。吸附热大，与化学反应的热效应接近，为化学吸附。

这里介绍两种吸附热的定义。

1）积分吸附热Q_i。在固体表面上恒温地吸附一定量的气体时所放出的热量称为积分吸附热。如果某吸附剂在恒温下吸附了a mol吸附质后，放出的总热量为Q，则积分吸附热Q_i为

其中，下标V^g表示与吸附剂相接触的吸附质气体在吸附过程中体积不变。

它表示在吸附平衡时，已经被气体覆盖的那部分表面的平均吸附热。它反映了吸附过程中一个比较长的时间内热量变化的平均结果。

2）微分吸附热Q_d。在已经吸附了一定的气体以后，固体表面上再吸附少量的气体da时所放出的热量为dQ。它反映了吸附过程中某一瞬间的热量变化。由于固体的不均匀性，吸附热随表面覆盖度θ的不同而改变，在覆盖度θ不同时，微分吸附热的值是不同的。因此，在吸附过程中，任一瞬间的Q_d并不相同。据此，Q_d为

因此，积分吸附热实际上是各种不同覆盖度下微分吸附热的平均值。

（2）吸附热的确定

1）量热方法。用热量计直接测定吸附热。

2）根据吸附等量线计算。在保持吸附量不变的情况下，测定平衡压力和温度的关系，也就是根据所谓吸附等量线，按克劳修斯-克拉贝龙（Clausius-Clapeyron）方程计算得到吸附热，即

积分得

或

由式（1-10）可以方便地计算出某吸附量下的吸附热。其中，Q_a为等量吸附热，它实际上是一种微分吸附热。

用克劳修斯-克拉贝龙方程计算Q_a的前提是把物理吸附过程等效为气体分子在固体表面的液化。如果过程可逆，则吸附热相当于液化热。因此温度和压力与相变热的关系应符合克劳修斯-克拉贝龙方程。

（3）吸附平衡与吸附量

1）吸附平衡。气相中的气体分子可以被吸附到固体表面上来，已被吸附的分子也可以脱附（解吸）而回到气相。在温度和吸附质的分压恒定的条件下，当吸附速率与脱附速率相等时，即单位时间内被吸附到固体表面上的量与脱附回到气相的量相等时，达到吸附平衡。此时固体表面的吸附量不再随时间而变。吸附平衡是一种动态平衡。

2）吸附量Γ。吸附达到平衡时单位质量的吸附剂吸附气体的物质的量或体积V（换算成气体在标准状态下所占的体积）称为吸附量，即

Γ＝V/m（Γ的单位为m³·g^-1和m³·kg^-1）或Γ＝n/m（Γ的单位为mol·g^-1和mol·kg^-1）

影响吸附量的因素有吸附剂和吸附质的本性、温度及达到吸附平衡时吸附质的分压等。

4.吸附曲线

吸附曲线主要反映固体吸附气体时，吸附量和温度、压力的关系。恒T过程，Γ＝f（p）为吸附等温式，可以得到吸附等温线；恒p过程，Γ＝f（T）为吸附等压式，可以得到吸附等压线；恒Γ过程，p＝f（T）为吸附等量式，可以得到吸附等量线。这三种吸附曲线是相互联系的，其中任何一种曲线都可以用来描述吸附作用的规律，实际工作中使用最多的是吸附等温线，最常用的有五种类型，如图1-8所示。

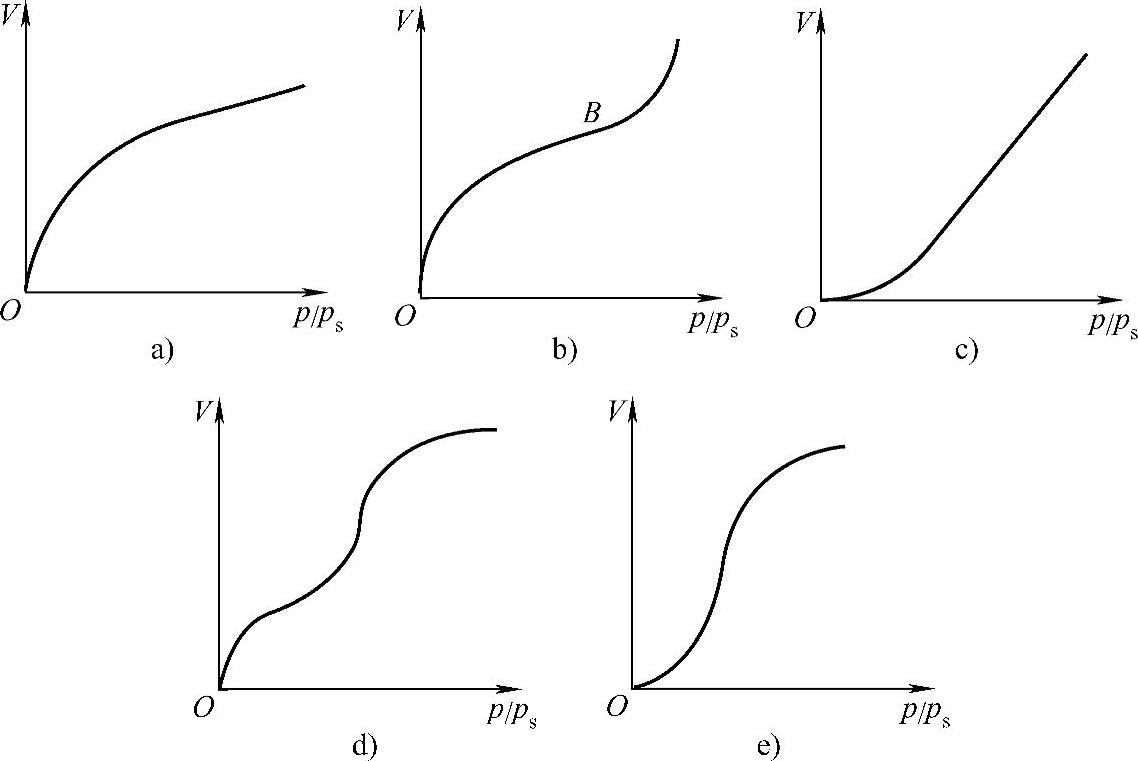
图1-8 最常用的吸附等温线

1）单分子吸附型等温线（图1-8a），化学吸附通常表现为这种等温线。吸附剂的孔径在1.5nm以下。此种等温线在压力远低于p_s时，固体表面就吸满了单分子层，此时的吸附量可称为饱和吸附量V_m。

2）反S形等温线，也常称为S形等温线（图1-8b）。吸附剂的孔径通常在10nm以上。物理吸附常表现出这种等温线，它的特点是在低压下首先形成单分子层吸附（相当于B点，此时的吸附量为V_m），随着压力的升高逐渐产生多分子层吸附，当压力相当高时，吸附量又急剧上升，这表明被吸附的气体已开始凝结为液相。根据凹液面的Kel-vin公式有

其中，对于凹液面r为负值。由此式可知，若吸附质液体可以润湿毛细孔孔壁，则吸附液膜在孔中形成凹形弯曲面，其平衡时的饱和蒸气压小于相同温度下平液面上的蒸气压，毛细孔越小，即∣r∣越小，p_r越小，因此对正常平液面未达到饱和的蒸气压，可以在毛细孔的弯曲液面上凝结，气体压力越高，能发生气体凝结的毛细孔越大，这种现象称为毛细凝结现象。这是多孔性固体所具有的特殊吸附现象。

3）如图1-8c所示，等温线是凹的，说明吸附质和吸附剂之间的相互作用很弱。但压力稍增大，吸附量即迅速增加。当压力接近于p_s时便和图1-8b所示）曲线相似，曲线成为与纵轴平行的渐近线，这表明吸附剂表面上的多层吸附逐渐转变为吸附质凝聚。

4）如图1-8d所示，等温线在低压下是凸的，表明吸附质和吸附剂有相当强的亲和力，并也易于确定类似于图1-8b的等温线B点的位置，相当于盖满单分子层时的饱和吸附量。随着压力的增大，又有多层吸附逐渐产生毛细管凝结，所以吸附量能够迅速增加。最后由于毛细孔中均装满吸附质液体，故吸附量不再增加，等温线又变得平缓。

5）如图1-8e所示，等温线低压下也是凹的，与图1-8c相似。随着压力的增大也产生多分子层和毛细管凝结，此种情况和图1-8d所示曲线的高压部分相似。

5.吸附等温式

（1）朗缪尔（Langmuir）吸附等温式——单分子层吸附理论 关于气体在固体上的吸附，早在1916年，朗缪尔就首先提出单分子层吸附模型，并从动力学观点推导了单分子层吸附方程式。他认为：当气体分子碰撞固体表面时，有的是弹性碰撞，有的是非弹性碰撞；若为弹性碰撞，则气体分子跃回气相，且与固体表面无能量交换；若为非弹性碰撞，则气体分子就“逗留”在固体表面上，经过一段时间又可能跃回气相。气体分子在固体表面上的这种“逗留”就是吸附现象。

1）朗缪尔基本假设。在推导单分子层吸附方程时，朗缪尔作了如下基本假设：

①气体在固体表面上的吸附是单分子层的。因此只有当气体分子碰到固体的空白表面时才能被吸附，这种碰撞是非弹性碰撞，如果碰到已被吸附的气体分子上则不发生吸附，它的碰撞是弹性碰撞。

②被吸附的分子间无相互作用力。被吸附分子脱附时，不受邻近吸附分子的影响。

③吸附剂表面是均匀的，表面上各吸附位置的能量相同。

④吸附平衡是动态平衡。

2）覆盖度。设吸附剂表面上有S个吸附位置，当有S₁个位置被吸附质分子占据时，则空白位置数为S₀＝S-S₁，令

式中 θ——覆盖度。

于是空白位置的分数为1-θ，当所有的吸附位置都被吸附质占据时，θ＝1。

3）吸附速率r_a。若以μ代表单位时间、单位固体表面上碰撞的气体分子数，即碰撞频率，则根据气体分子运动论有

式中 p——气体压力；

m——气体分子的质量；

k——玻耳兹曼（Boltzmann）常数；

T——热力学温度。

根据基本假设①，吸附速率应与空白位置分数和碰撞频率成正比，则

式中 k_a——吸附速率系数（吸附速率常数）。

4）脱附速率r_d。根据基本假设②，单位时间、单位面积上脱附的分子数与覆盖度成正比，于是

式中 k_d——脱附速率系数。

吸附平衡时，根据基本假设④，r_a＝r_d，可得

5）朗缪尔吸附等温式。整理后得朗缪尔吸附等温式为

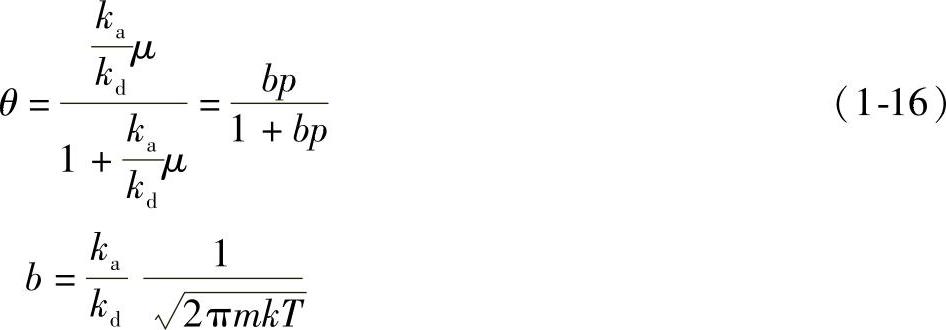
式中 b——吸附系数，它的大小代表了固体表面吸附气体能力的强弱。

若V_m表示单位质量吸附剂的表面覆盖度θ＝1时的吸附量，即饱和吸附量（又称极限吸附量），以V表示单位质量吸附剂在气体压力为p时的吸附量（该吸附量换算成气体在标准状态下的体积），则

于是朗缪尔吸附等温式改写为

(www.xing528.com)

式中 b——吸附系数。

如果一个分子被吸附时放热q，则被吸附分子中具有q以上能量的就能离开表面到气相中。根据玻尔兹曼（Boltzmann）能量分布原理[阿伦尼乌斯（Arrhenius）公式]，返回气相及脱附的分子数（速度常数）与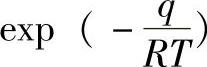成正比，即

式中 A——比例系数。将式（1-19）代入式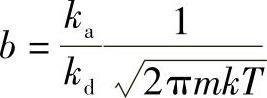，得

由式（1-20）可见，b是温度和吸附热的函数。b随吸附热增加而增大，随温度升高而减小。所以一般温度升高，吸附量降低。

从朗缪尔吸附等温式可以看到：

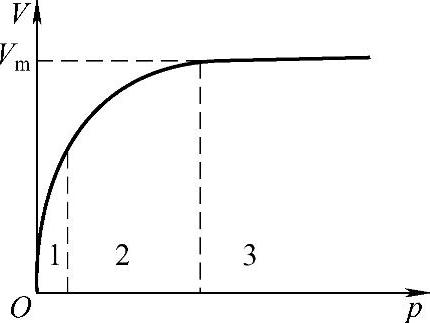
图1-9 朗缪尔吸附等温式

①在压力足够低或吸附较弱时，bp≪1，则V≈V_mbp（满足y＝kx函数），这时吸附量V与p成直线关系，如图1-9的低压部分（1部分）所示。

②压力足够大或吸附较强时，bp≫1，则V＝V_m。这时V与p无关，吸附达到单分子层饱和状态，如图1-9所示的3部分。

③当压力适中时，V与p成曲线关系，如图1-9中曲线部分（2部分）所示。

6）朗缪尔吸附等温式的应用。将朗缪尔吸附等温式改写为

这是朗缪尔吸附等温式的又一表示形式。p/V与p成线性关系，通过试验可测定不同p下的吸附量V，以p/V～p作图得一直线，直线的斜率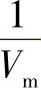为，截距为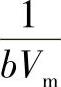，从斜率和截距求出吸附系数b和铺满单分子层的气体体积V_m。

V_m是一个重要参数。若已知每个吸附质分子的截面面积A_m，就可计算吸附剂的总表面积S和比表面积A₀，即

式中 S——吸附剂的总表面积；

A_m——^一个吸附质分子的截面面积；

N_A——阿伏伽德罗常数；

n——吸附质的物质的量。

标准状态下，气体的摩尔体积为22400cm³·mol^-1，若V_m的单位采用cm³，则n＝V_m/（22400cm³·mol^-1）（标准状态）。

可得比表面积A₀为

吸附热变化不大、覆盖度较小的绝大多数化学吸附均能较好地服从朗缪尔假设，从而符合朗缪尔吸附等温式。压力较大的物理吸附，会发生多层吸附，因而不遵循朗缪尔吸附等温式。有些半径在几纳米以下的微孔吸附剂，虽然是多分子层吸附，但吸附等温线也与图1-8a相似。

7）混合气体的吸附等温式。在气相中含有两种或两种以上的气体物质，它们都能在固体表面上形成单分子层吸附，这种混合吸附情况常见于多相催化。

当A和B两种粒子都被吸附时，设A、B两种气体在固体表面上的吸附系数分别为b_A和b_B。在分压分别为p_A和p_B时，固体表面的覆盖度分别为θ_A和θ_B。A和B分子的吸附速率与脱附速率分别为

达到吸附平衡时，A和B各自的吸附速率和脱附速率相等，则有

两式联立解得θ_A和θ_B分别为

可见，两种气体混合吸附时，将相互抑制。p_B增大使θ_A变小，即气体B的存在可使气体A的吸附受到抑制。同理，气体A的吸附也要妨碍气体B的吸附。

对于多种气体混合物的吸附，其中组分i气体的朗缪尔吸附等温式为

在上面的朗缪尔吸附等温式中虽然所写的是θ和p之间的关系，但因为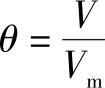，所以实际上也是V和p的关系（V是吸附气体的体积）。

8）朗缪尔吸附等温式的缺点。

①假设吸附是单分子层的，与事实不符。

②假设表面是均匀的，其实大部分表面是不均匀的。

③在覆盖度θ较大时，朗缪尔吸附等温式不适用。

（2）BET吸附等温式——多分子层吸附理论 正因为朗缪尔吸附等温式具有局限性，所以许多吸附等温线不符合朗缪尔吸附等温式，原因是不符合单分子层吸附假设，尤其是物理吸附，大多数是多分子层吸附。

1938年，由布鲁尼尔（Brunauer）、埃密特（Emmett）、特勒（Teller）三人在朗缪尔单分子层吸附理论的基础上，提出的多分子层吸附理论，简称BET理论，其导出公式称为BET吸附等温式。

1）BET理论的基本假设。

①吸附可以是多分子层的。该理论认为，在物理吸附中，不仅吸附质与吸附剂之间有范德华引力，而且吸附质之间也有范德华引力，因此，气相中的分子若碰在吸附分子上，也有可能被吸附，所以吸附是多分子层的。

②固体表面是均匀的。多层吸附中，各层都存在吸附平衡，此时吸附速率和脱附速率相等。不必上层吸附满后才吸附下层。

③除第一层以外，其余各层的吸附热等于吸附质的液化热。

2）BET吸附等温式为

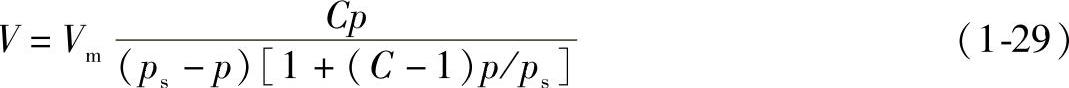
式中 V_m——铺满单分子层所需气体的体积；

C——与吸附热有关的常数；

p、V——吸附时的压力和体积；

p_s——试验温度下吸附质的饱和蒸气压。

该式又称为二常数公式，常数是V_m和C。为了使用方便，将二常数公式改写为

从试验可测定不同p下的吸附量V，再用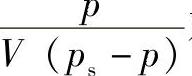对绘图，若得一条直线，则说明该体系符合BET公式。从直线的斜率和截距可计算两个常数C和V_m的值。

根据式（1-22）和式（1-23），从V_m可以计算吸附剂的总表面积S和比表面积A₀。

3）BET吸附等温式的使用范围。BET吸附等温式通常只适用于比压（p/p_s）控制在0.05～0.35的情况，这是因为在推导公式时，假定是多层的物理吸附。比压太低（p/p_s＜0.5），压力太小，不能建立起多分子层物理吸附，甚至连单分子层物理吸附也远未完全形成。比压过高（p/p_s＞0.35），容易发生毛细凝聚，因而破坏了多层物理吸附平衡，使结果偏高。

（3）弗罗因德利希（Freundlich）吸附等温式 弗罗因德利希在大量试验的基础上，总结出经验公式为

式中 V、p——吸附平衡时的吸附量与吸附质气相分压；

n、k——经验常数，n一般大于1。

将式（1-31）取对数，得

6.影响气-固界面吸附的因素

影响气-固界面吸附的因素有多种，现作简单介绍。

（1）温度 气体吸附一般是放热过程，因此无论物理吸附还是化学吸附（有例外），温度升高时，吸附量是减少的。可根据需要确定最适宜的温度，并不是越低越好。

在物理吸附中，要有明显的吸附作用，一般温度控制在气体的沸点附近。例如常用的吸附剂活性炭、硅胶、Al₂O₃等，对吸附质N₂要在其沸点-195.8℃附近才能进行吸附，对吸附质He要在其沸点-268.3℃才能进行吸附，而在室温下这些吸附剂都不吸附He和N₂或空气，所以气相色谱试验中常用He或N₂作载气。

在化学吸附中，情况比较复杂。例如H₂（沸点为-252.5℃）在室温下，不被上述吸附剂所吸附，但在Ni或Pt上则被化学吸附。

温度不仅影响吸附量，还能影响吸附类型。如H₂在MgO-Cr₂O₃催化剂上的吸附，在-78℃时为物理吸附，而在100℃时为化学吸附。

（2）压力 无论是物理吸附还是化学吸附，增大吸附质平衡分压，吸附速率和吸附量都是增加的。

（3）吸附剂和吸附质的性质 遵循相似相吸的规则，即极性吸附剂易于吸附极性吸附质，非极性吸附剂易于吸附非极性吸附质。如活性炭是非极性吸附剂，故其对烃类和各种有机蒸气的吸附能力较强。但活性炭的界面含氧量增加时，其对水蒸气的吸附量将增大。又如硅胶、硅铝催化剂、Al₂O₃等是极性吸附剂，易于吸附极性的水、氨、乙醇等吸附质。

无论是极性还是非极性吸附剂，一般吸附质分子的结构越复杂，沸点越高，被吸附的能力越强。这是因为分子结构越复杂，范德华引力越大；沸点越高，气体越易凝结，这些都有利于吸附。

酸性吸附剂易吸附碱性吸附质，反之碱性吸附剂易吸附酸性吸附剂。例如，硅铝催化剂、分子筛等均为酸性吸附剂或固体酸催化剂，故它们易吸附碱性气体，如NH₃、水蒸气和芳烃蒸气等。

（4）多孔性吸附剂的孔结构 多孔性吸附剂的孔隙大小不但影响吸附速率，还直接影响吸附量的大小。硅胶是极性吸附剂，有很大的吸水能力，但若将硅胶进行扩孔，则比表面积大大减小，从而对水蒸气的吸附量也大大减小。

7.固-液界面的吸附

（1）固-液界面吸附的特点

1）溶液吸附规律比较复杂。固体自溶液中的吸附是最常见的吸附现象之一。溶液吸附规律比较复杂（这主要是因为溶液中除了溶质外还有溶剂），因而固体自溶液中吸附的理论不像气体吸附那样完整，至今仍处于初始阶段。固体对气体的吸附，主要由固体表面与气体分子相互作用的强弱来决定。而固体自溶液中的吸附，至少要考虑三种作用力，即在界面层上固体与溶质之间的作用力、固体与溶剂之间的作用力以及在溶液中溶质与溶剂之间的作用力。当比表面积较大的固体在溶液中吸附任意溶质或溶剂时，存在着竞争性优先吸附或顶替吸附现象。一般固体对溶液中的溶质和溶剂均能吸附，由于固体与溶剂和溶质的相互作用会有差异，因此溶液在界面吸附层的浓度与体相（溶液内部）的浓度不一致。如果固体表面上的吸附溶质浓度比体相（溶液内部）的大，则对溶质就是正吸附，否则就是负吸附。

2）溶液中的吸附速率较慢。从吸附速率看，溶液中的吸附速率一般比气体吸附速率慢得多，这是由于吸附质分子在溶液中的扩散速度比在气体中慢。在溶液中，固体表面总有一层液膜，溶质分子必须通过这层膜才能被吸附，再加上孔的因素，因此吸附速率就更慢了，这意味着溶液吸附平衡时间往往很长。

溶液吸附的应用极为广泛，例如常见的活性炭脱色、岩石对表面活性剂的吸附等，它们不仅具有研究的理论意义，更有巨大的使用价值。为了更好地解决实际问题，人们必须掌控在不同情况下吸附的基本规律。

（2）固体自溶液中的吸附量 溶液吸附虽然比气体吸附复杂，但测定吸附量的试验方法却比较简单。只要将一定量的固体放入一定量的已知浓度溶液中，不断振荡，当吸附达到平衡后，测定溶液的浓度，从浓度的变化就可以计算单位质量固体吸附了多少溶质。设c₀和c分别表示吸附前、后溶液的浓度，V是溶液的体积，m是吸附剂的质量，则溶质的吸附量Γ为

式中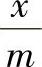——每克吸附剂上吸附溶质的量（mol·g^-1）。

这种计算没有考虑溶剂的吸附，所以通常称为表观吸附量。如果是稀溶液，表观吸附量与真实的接近，但对于浓溶液必须了解表观吸附量与真实吸附量之间的关系。在溶液吸附中，溶液的平衡浓度c和吸附量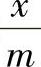之间的定量关系目前尚不能由理论导出，但考虑到液相吸附和气相吸附有许多相似之处，人们常利用气相吸附的关系式（如弗罗因德利希公式、朗缪尔公式和BET公式）来处理液相吸附结果。因为这些公式是“借用的”，公式中常数的物理意义不很明确，故只能作为经验公式。实际使用时只要把公式中的p改为c，相对压力p/p_s改为c/c₀即可，此处c₀为饱和溶液的浓度。

（3）固体自溶液中吸附的影响因素 固体自溶液中的吸附有着广泛的应用，其研究工作越来越深入。然而由于体系的复杂性，至今仍处在数据积累阶段，没有完善的理论，但从大量试验中得出了一些经验规律，下面将作简要介绍。注意在讨论某一影响因素的规律时，是以其他因素一定为前提的。

1）温度。与固体吸附气体一样，固体自溶液中的吸附是放热过程，因此，一般温度升高，吸附量减少。但对于溶解度不高的体系，还要考虑溶解度与温度的关系。这是因为温度升高，溶解度增大，故饱和溶液浓度增大。该因素引起的吸附量增加超过了温度升高而使吸附量减少的作用，总结果是吸附量随温度升高而增加。

2）溶解度。溶解度越小的溶质越易被吸附。此规则要在其他条件相同或相近的情况下才可以应用。

3）吸附剂、溶质和溶剂三者的性质。固体自溶液中吸附一般也服从相似相吸的规则：极性吸附剂易吸附极性溶质，非极性吸附剂易吸附非极性溶质。在应用此规则时，要同时考虑吸附剂、溶质和溶剂三者之间的关系。通常，极性溶质易溶于极性溶剂，非极性溶质易溶于非极性溶剂。因此，从溶解度角度来看，极性溶质易于从非极性溶剂中被吸附，非极性溶质易于从极性溶剂中被吸附。综上所述，可知：极性吸附剂易于从非极性溶剂中吸附极性溶质，非极性吸附剂易于从极性溶剂中吸附非极性溶质。

还可以得到有关极性有机物同系物吸附的规律，即特劳贝（Traube）规则：吸附量随碳氢链增长而有规律地增加。例如，活性炭自水溶液中吸附脂肪酸时，吸附量的顺序为：丁酸＞丙酸＞乙酸＞甲酸（链越短，极性越强）。因为活性炭是非极性吸附剂，而非极性吸附剂总是易于自极性溶剂中优先吸附非极性组分。

同样，硅胶自四氯化碳中吸附脂肪醇吸附量的顺序为：乙醇＞正丙醇＞正戊醇＞正己醇﹥正辛醇（链越短，极性越强），这也符合“极性吸附剂易于从非极性溶剂中吸附极性溶质”这一规律。当然由于体系性质不同，吸附量顺序正好与前一个例子相反，所以有时也称为反Traube规则。

关于吸附剂的极性与非极性，应注意概念的相对性。例如，活性炭自水溶液中吸附时是非极性吸附剂，但自四氯化碳（典型的非极性溶剂）中吸附时，活性炭会表现出极性吸附剂的性质。与此相应必然有以下的结果：活性炭自非极性溶剂吸附有机同系物时吸附量随碳链增长而减少。这是因为活性炭的表面覆盖有氧化物，这些氧化物是极性的。在极性强的水中吸附时，这些表面氧化物的极性不能明显地显示出来，于是活性炭表现为非极性吸附剂的特征，但在非极性的四氯化碳中吸附时，这些表面氧化物的极性就突现出来。所以Traube规则是个相对规则。

4）吸附剂孔径的大小。对多孔吸附剂来说，孔径越小，向孔内扩散速率越慢，吸附平衡时间越长，且只有尺寸小于孔径的溶质分子才能被吸附。

5）盐。即使加入的盐不被吸附，但由于它能影响溶质与溶剂之间的相互作用，因此也会对吸附产生明显的影响。试验证明，若盐能使溶质的溶解度减小，则吸附量会因盐的加入而增大；反之，若盐能提高溶质的溶解度，则吸附量会因盐的加入而减小。

6）多种溶质溶液中的其他溶质。若溶液中有多种溶质，且均能被吸附，则除非有特殊相互作用，通常各溶质的吸附要比其在同条件下单独存在时吸附量小，可用混合吸附公式表示。

溶液吸附中的规律非常复杂，影响因素很多，而且这些因素不是相互独立的。在探讨吸附机理和预测各种吸附情况时，必须根据具体情况，综合考虑各种因素，才能得出正确的结论。