互换装配法：工业制造的新趋势

互换装配法是从制造合格的同规格零件中任取一个用来装配均能达到装配精度要求的装配方法。

互换法装配产品的装配精度是靠控制零件的加工精度来保证的，因此需要零件的制造满足互换性。

互换装配法的优点：

（1）装配工作简单、生产率高；

（2）有利于组织流水生产；

（3）便于将复杂的产品在许多工厂中协作生产；

（4）有利于产品的维修和配件供应。

互换装配法的缺点：难以适应装配精度要求很高的场合。

按互换程度的不同，互换装配法分为完全互换装配法与不完全互换装配法。

1）完全互换装配法

在产品装配时各组成环零件不需要挑选或改变其大小或位置，全部产品装配后即能达到封闭环的公差要求，这种装配方法称为完全互换装配法。

完全互换装配法采用极值法计算。为保证装配精度要求，尺寸链中封闭环的极值公差应小于或等于封闭环的公差要求值。

完全互换法计算方法见“7.5.3装配尺寸链的计算”，下面再举例说明。

【实例9-1】在图9-22所示装配关系中，轴是固定的，齿轮在轴上回转，要求保证齿轮与挡圈之间的轴向间隙为0.10～0.35 mm。已知A1=30 mm、A2=5 mm、A3=43 mm、A4=（标准件）、A5=5 mm。现采用完全互换法装配，试确定各组成环的极限偏差。

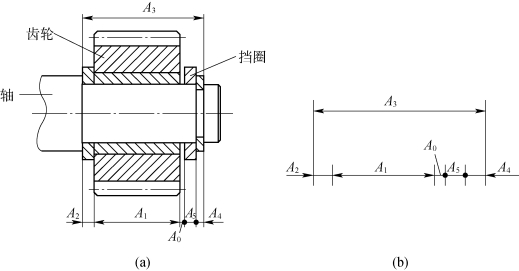
图9-22　齿轮轴装配图及其尺寸链

（a）装配图；（b）尺寸链

解：（1）画装配尺寸链，判断封闭环、增环和减环，校验各环基本尺寸。根据题意，轴向间隙为0.10～0.35 mm，则封闭环尺寸，公差T0=0.25 mm。装配尺寸链如图9-23（b）所示，尺寸链总环数n=6。其中，尺寸A3为增环，尺寸A1、A2、A4、A5为减环。封闭环的基本尺寸为

A0=A3-(A1+A2+A4+A5)

=43-(30+5+3+5)=0 mm

由计算可知，各组成环基本尺寸的已定数值是正确的。

（2）确定协调环。A5是挡圈尺寸，易于加工，且可以用通用量具测量，因此选它作为协调环。

（3）确定除协调环以外各组成环的公差和极限偏差。按等公差法分配各组成环平均公差

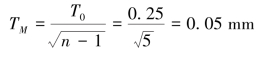
参照国家标准，并考虑各零件加工的难易程度，在各组成环平均公差TM的基础上，对各组成环的公差进行合理调整，并按入体原则标注。轴用挡圈A4是标准件，其尺寸为。其余各组成环的公差按加工难易程度调整如下：

T1=0.06 mm,T2=0.02 mm,T3=0.1 mm

故取：。

（4）计算协调环的公差和极限偏差。协调环的公差为

T5=T0-(T1+T2+T4+T5)=0.25-(0.06+0.02+0.1+0.05)=0.02 mm

协调环的下偏差为

ES0=ES3-(EI1+EI2+EI4+EI5)

0.35=0.1-(-0.06-0.02-0.05+EI5)(www.xing528.com)

EI5=-0.12 mm

协调环的上偏差为

ES5=T5+EI5=0.02+(-0.12)=-0.10 mm

因此，协调环的尺寸为。

综上所述，各组成环的尺寸和极限偏差为：

2）大数互换法

大数互换法又称为不完全互换法，是指在绝大多数产品中，装配时各组成环不需要挑选或不需要改变大小或位置，装配后即能保证装配精度要求的装配方法。

大数互换法与完全互换法相比，放宽了尺寸链各组成环的公差，有利于零件的经济加工，但同时会有少部分产品的装配精度超差，需要进行返修。因此，大数互换法多用于大批大量生产和装配精度要求不太高而组成环数较多的装配尺寸链。

大数互换法采用的基本理论是概率论，即按所有零件尺寸分布曲线的状态来处理。通常封闭环的尺寸分布趋近正态分布，其尺寸分散范围为±3σ，产品合格率为99.73%。采用大数互换法装配时，尺寸链的计算一般采用概率法，详见“7.5.3装配尺寸链的计算”。下面再以齿轮轴为例详细说明。

【实例9-2】如图9-23所示，要求保证齿轮与挡圈之间的轴向间隙为0.10～0.35 mm。已知A1=30 mm、A2=5 mm、A3=43 mm、A4=（标准件）、A5=5 mm。现采用大数互换法装配，试确定各组成环的极限偏差。

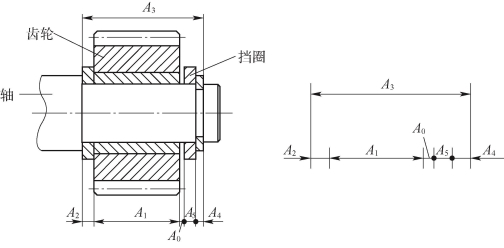
图9-23　齿轮轴装配图及其尺寸链

解：（1）画装配尺寸链，判断增、减环，校验各环基本尺寸分析计算过程与上例中1）相同。

（2）确定协调环。考虑到A3较难加工，希望其公差尽可能大，故选用A3作为协调环，最后确定其公差。

（3）确定除协调环以外各组成环的公差和极限偏差。假设5个组成环均接近正态分布，则各组成环的平均公差为

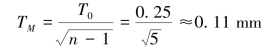
参照国家标准，并考虑各零件加工的难易程度，在各组成环平均公差TM的基础上，对各组成环的公差进行合理调整，并按“入体原则”标注。轴用挡圈A4是标准件，其尺寸为。其余各组成环的公差按加工难易程度调整如下：

T1=0.14 mm,T2=0.05 mm,T5=0.05 mm

故取：。

（4）计算协调环的公差和极限偏差。

①计算协调环的公差。

②计算各环平均尺寸，并求出协调环的尺寸和极限偏差。各环平均尺寸为

A1M=29.93 mm,A2M=A5M=4.975 mm,A4M=2.975 mm,A0M=0.225 mm

因

A0M=A3M-(A1M+A2M+A4M+A5M)

A3M=A0M+(A1M+A2M+A4M+A5M)

=0.225+(29.93+4.975+2.975+4.975)

=43.08 mm

所以，协调环的尺寸和极限偏差为

综上所述，各组成环的尺寸和极限偏差为：