装配尺寸链计算实例优化

【实例7-9】图7-32为齿轮箱部件，装配后要求轴向窜动量为0.2～0.7 mm，即A0=。已知其他零件的有关基本尺寸是：A1=122 mm、A2=28 mm、A3=5 mm、A4=140 mm、A5=5 mm，试决定其上下偏差。

图7-32　齿轮箱装配图及装配尺寸链

解：1）极值解法

（1）画出装配尺寸链，如图7-29所示，校验各环基本尺寸。封闭环基本尺寸为基本尺寸正确。

（2）确定各组成环尺寸的公差大小和分布位置。为了满足封闭环公差要求T0=0.5 mm，各组成环公差Ti的累积值∑Ti不得超过此0.50 mm值，即应满足

∑Ti=T1+T2+T3+T4+T5≤T0=0.50 mm

问题：如何既方便又经济合理地分配确定各组成环的公差Ti？

通常，把封闭环公差（T0=0.5 mm）分配到各组成环公差（Ti）的方法有3种：公差大致相等、精度大致相等和加工难易程度大致相同。

①按等公差分配法。即将T0平均分摊到各个组成环Ti

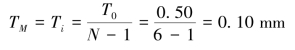
再按公差分配的“入体原则”，确定各组成环的上下偏差

A4作为该尺寸链的“协调环”，即A4的上、下偏差应通过计算获得

+0.70=(0.10+0.10)-(-0.10+ΔxA4-0.10),δxA4=-0.30 mm+0.20=(0+0)-(0+ΔsA4+0),ΔsA4=-0.20 mm

故A4=mm。

进行验算：T0=T1+T2+T3+T4+T5=0.10+0.10+0.10+0.10+0.10=0.50 mm，计算结果符合装配精度要求。

等公差法计算方便，但未考虑各零件的基本尺寸差异，因此各零件的精度等级不同，显然不太合理。在同一尺寸链中基本尺寸大致差不多的情况下，此法应用广泛。

②按等精度分配法。假定这台机器中每个零件都是同样的精度等级，则分配公差时，凡基本尺寸大的零件分配公差较大，反之较小，这较为合理。

据《公差与技术测量》，公差

T=aI

式中，a——公差等级系数；

I——公差单位，，而D=，A、B分别为尺寸分段的首尾两个尺寸值。

用等精度法分配公差时，可查表得出该尺寸链中各组成环基本尺寸相应的公差单位值，再求出平均公差等级系数。

③按加工难易程度分配法。根据零件要求和加工要求来分配公差，是更为科学合理的方法。但需要设计人员有较丰富的经验。(www.xing528.com)

如上例中：A1、A2加工较难，精度等级应略为降低。A3、A5加工方便，可适当提高精度等级。A4加工难度中等。按等精度中求得平均精度等级为IT10。

今取A1、A2大于10级，而A3、A5取9级，即

TA1=0.17 mm　TA2=0.1 mm　TA3=TA5=0.3 mm

TA4=T0-(T1+T2+T3+T5)=0.17 mm

取A4为协调环，其余组成环分别为：A1=，A2=，A3=A5=。则协调环A4=。

结果符合装配后封闭环的技术要求。

2）概率解法

当装配精度要求较高，而尺寸链的环数又较多（大于4环）时，应采用概率解法。

按等精度分配公差的概率解法，因为概率解法中的封闭环

所以平均公差等级系数

因为127≈64×2，所以平均公差等级系数几乎是放大了一倍。

所以T1=2.52×127=320=0.32 mm

T2=1.31×127=160=0.16 mm

T3=T5=0.73×127=90=0.09 mm

T4=2.52×127=320=0.32 mm

仍以A4为“协调环”，按“入体原则”将其余组成环写成偏差形式，即

求协调环A4的平均基本尺寸

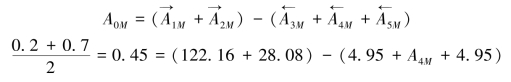
得

所以

验算：T0≤0.50 mm，满足要求。

注意：以互换法解尺寸链所允许的公差较小，当在规定的生产条件下难以加工时，应采用其他装配方法。