如何用概率法解尺寸链？

极值解法的优点：简便、可靠、可保证不出现不合格品；缺点：根据T0=ES0-EI0=关系式分配给各组成环的公差过于严格，甚至无法加工，因此不够科学、不够合理。

概率解法可以克服极值解法的缺点，使其应用更为科学、合理。

1）概率解法的数学依据

在大批、大量生产中，一个尺寸链中的各组成环尺寸的获得，彼此并无关系，因此可将它们看成是相互独立的随机变量。经大量实测数据后，从概率的概念来看，有两个特征数：

（1）算术平均值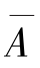——这数值表示尺寸分布的集中位置，如图7-14所示；

（2）均方根偏差δ——这数值说明实际尺寸分布相对算术平均值的离散程度。

独立随机变量之和的均方差为

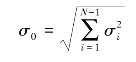
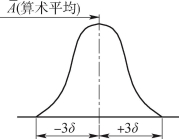
图7-14　算术平均值

其中：σi=（Ai-）。

这是用概率法解尺寸链的数学基础，它反映了封闭环误差与组成环误差间的基本关系。

2）各环公差计算

公式σ0=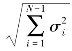反映了封闭环误差与组成环误差间的基本关系。

由于尺寸链计算时，不是均方根偏差间的关系，而是以误差量（或公差）间的关系来计算的，因此上述公式须改写成其他形式。当零件尺寸为正态分布曲线时，其偶然误差ε与均方根误差σ间的关系，可表达为ε=6σ，即

(www.xing528.com)

若尺寸链中各组成环的误差分布，都遵循正态分布规律，则其封闭环也将遵循正态分布规律。若取公差带T=6σ，则封闭环的公差与各组成环的公差关系可表示为

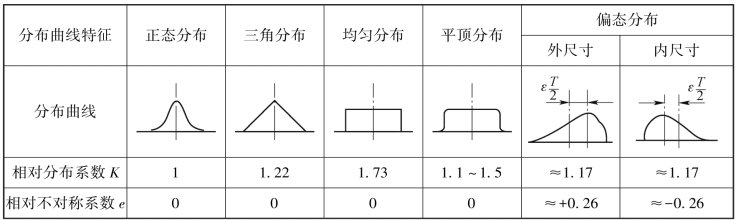
当零件尺寸分布下为非正态分布时，封闭环公差计算时须引入“相对分布系数K”。K表示所研究的尺寸分布曲线的不同分布性质，即曲线的不同分布形状。

正态分布时：T=6σ，σ=；非正态分布时：σ=K。所以，封闭环公差的一般公式为

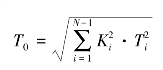
各种K值可参考表7-1。

表7-1　一些尺寸分布曲线的K及e值

若各组成环公差相等，即令Ti=TM时，则可求得各环的平均公差为

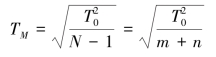
而极值解法的。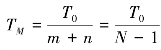

在计算同一尺寸链时，用概率解法可将组成环平均公差扩大倍。但实际上，由于各组成环通常未必是正态分布曲线，即Ki＞1，故实际所求得的扩大倍数比小些。

用概率解法可将组成环平均公差扩大倍的原因：极值解法时的是包括了封闭环尺寸变动时一切可能出现的尺寸，即尺寸出现在范围内的概率为100%；而概率解法时的TM=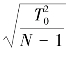是正态分布下取误差范围内的尺寸变动，即尺寸出现在该范围内的概率为99.73%，由于超出之外的概率仅为0.27%，这个数值很小，实际上可认为不至于出现，因此取作为封闭环尺寸的实际变动范围是合理的。正态分布下取误差范围内的尺寸变动如图7-15所示。

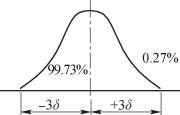
图7-15　正态分布下取误差范围内的尺寸变动