数值与码：十进制和二进制的转换

1.数值

数值可以表示长度、质量、时间、温度等物理量的大小程度。

表示数值大小的各种计数方法称为计数体制，简称数制。按进位的原则进行计数称进位计数制。常用的数制有十进制、二进制、十六进制等。每一种进制有一组特定的数码，如十进制数有0、1、2、…、9共10个数码。数码总数称为基数，如十进制基数是10。每位数的“1”代表的值称为权，如十进制各位的权分别是10⁰、10¹、10²、…及10^-1、10^-2、10^-3、…等。

二进制数的数码有“0”、“1”两个，基数是2，每位的权是2的幂，如2⁰、2¹、2²、…及2^-1、2^-2、…等，进位规则是“逢二进一”。

数字电路中，存在高、低电平两种工作状态，可以方便地表示二进制数（对于正脉冲，高电平为“1”低电平为“0”）。因此数字电路中普遍使用二进制。

日常生活中，人们习惯使用的是十进制数。十进制数可以和二进制数按数值的大小相互等值转换。

二进制数转换成十进制数的方法是按权展开，再求各位数值之和。

表10-1 20以内的十进制数与二进制之间的关系

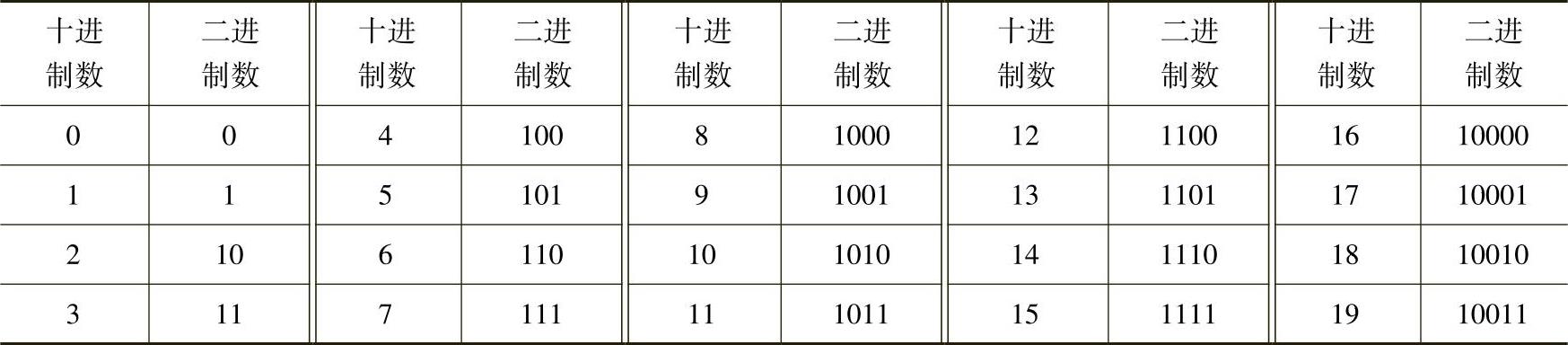
【例10.1】将二进制数11011转换为十进制数。

解：（11011）2=1×2⁴+1×2³+0×2²+1×2¹+1×2⁰

=16+8+0+2+1=（27）₁₀

十进制整数转换为二进制数的常用方法是除二取余法，即将十进制数连续除以2，并依次记下余数，一直除到商为0为止。以最后所得的余数为最高位，依次从后向前排列即为转换后对应的二进制数。

【例10.2】将十进制数218转换为二进制数。

解：用竖式除法表示除二取余法的过程。转化结果为图10-4所给出的二进制数与十进制数的对照表。

【例10.3】把（1011.11）B转换成二进制数（保留两位小数）。

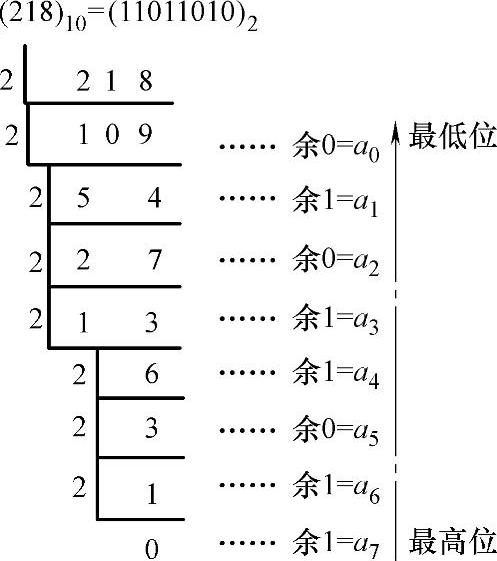
图10-4 例10.2图(www.xing528.com)

解：

（1011.11）B=1×2³+0×2²+1×2¹+1×2⁰+1×2^-1+1×2^-2

=8+0+2+1+0.5+0.25=（11.75）_D

（0.75）D=（0.11）_B

2.码

数字系统中的信息，除数据外还包括文字、符号和各种对象、信号等，这些信息都是用若干位“0”和“1”组成的二进制数表示的。这些二进制数分别称为十进制数码、文字、符号和某对象、信号等的代码。

n位二进制数，可以组成N=2ⁿ种不同的代码，代表2ⁿ种不同的信息或数据。

（1）二—十进制码（BCD码）组成十进制数的数码共有10个，至少需要4位二进制数表示。而4位二进制数码可以有16种组合，表示十进制数码时，只需用10种，有6种不用，故有多种表示方案。常用的二—十进制码有8421码、余3码、格雷码等。

每组（4位）二—十进制码表示一位十进制数，M位十进制数需用M组4M位二—十进制码表示。例如（16）10=（00010110）8421码。

842l BCD码是最基本、常见的BCD码，选用了4位二进制数的前10种组合。每组（4位）内8421码符合二进制规则，而组与组之间则是十进制。

表10-28421 BCD码及其所代表的十进制数

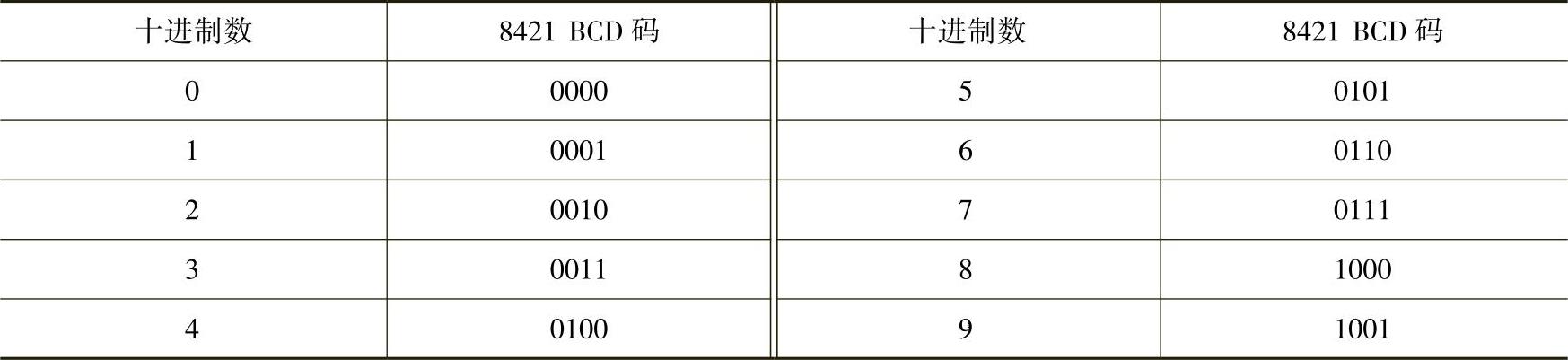
二—十进制码与自然二进制数形式相似，但本质不同。二进制数是按二进制的规则表示数值的大小，而二—十进制码是用二进制数表示十进制数码，它们的值并不一定相等，实际上往往不等。例如：（0110）8421码=（0110）2，但（0110）余3码≠（0110）2，（00010110）8421码≠（00010110）2。

（2）字符码 目前广泛应用的表示字母、符号的二进制代码是ASCII码（American Standard Code for Information Interchange，美国信息交换标准代码）。

ASCII码采用7位二进制数编码，可以表示128个字符。扩展ASCII码采用8位二进制数编码，可以表示256个字符。

在汉字系统中，由于中文文字较多，需用16位二进制数编码。

（3）其他代码 在数字系统中，任何信息包括各种特定的对象、信号等都要转化为二进制代码来处理。例如：在计算机的VGA/TVGA显示系统中，标准彩色字符的颜色与3位二进制代码对应，红色对应（100）2，而（010）2则代表绿色。