如何判断RLC串联电路的电压值是否与基尔霍夫定律矛盾？

1.谐振条件

串联谐振的条件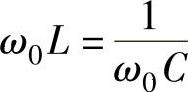：，即串联电路的电抗为零。由谐振条件导出了谐振时的电路频率。

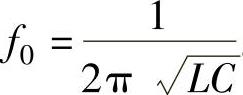使RLC串联电路发生谐振的方法有：

（1）调整信号源的频率，使之等于电路的固有频率；

（2）信号源的频率不变时，可以改变电路中的L值或C值的大小，使电路的固有频率等于信号源的频率。

2.串联谐振特征

串联电路的谐振特征有：

（1）电路发生串联谐振时，电路中阻抗最小，为电阻特性，且等于谐振电路中线圈的电阻R；

（2）若串联谐振电路中的电压一定，由于阻抗最小，因此电流达到最大，且与外加电压同相位；

（3）电感和电容元件两端的电压大小相等、相位相反，且数值等于输入电压的Q倍（其中Q是串联谐振电路的品质因数）

3.串联谐振电路的品质因数Q与电路的频率特性曲线的关系(www.xing528.com)

串联谐振电路的品质因数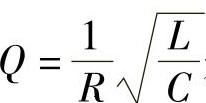是分析谐振电路时常用到的一个重要的性能指标。根据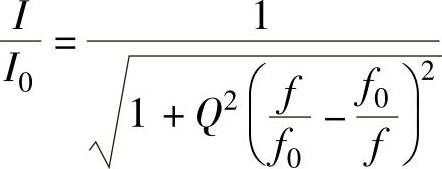

I可知，电流相对值随频率相对值变化的关系仅仅取决于电路

I₀的品质因数Q。

由图3-32也可看出，Q值对谐振曲线尖锐程度的影响很大：当频率偏离谐振频率不多时，电流值也偏离谐振电流，Q值越高，谐振曲线的顶部越尖锐，即电流衰减得越厉害，说明Q值大的电路对不是谐振频率的其他频率的信号抑制能力很强，即信号的选频性能好；而Q值越小，谐振曲线的顶部越圆钝，即电流偏离谐振电流时衰减不多，说明电路对不是谐振频率的其他频率的信号抑制能力较差，电路的选频性能差。

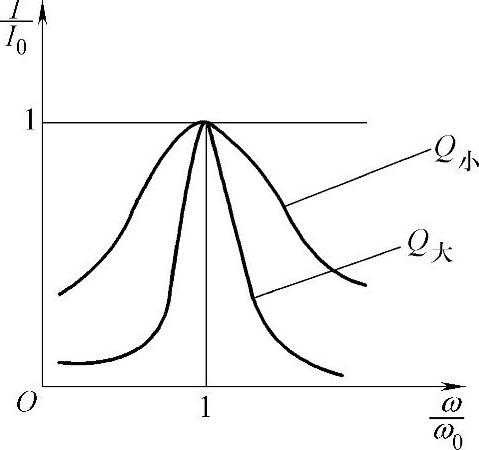
图3-32 I-ω谐振曲线

而通频带则是指以电流衰减到谐振电流I₀的0.707倍为界限时的一段频率范围。显然Q值越高，谐振曲线越尖锐，电路的选择性越好，但电路的通频带会因此变窄，从而容易造成传输信号的失真；而Q值越低，谐振曲线越平滑，电路的选择性能将因此而变差，但通频带越宽，传输的信号越不容易失真。

【例3.11】已知RLC串联电路的品质因数Q=200，当电路发生谐振时，L和C上的电压值均大于回路的电源电压，这是否与基尔霍夫定律有矛盾？

解：由于品质因数高的缘故而使储能元件两端在串谐发生时出现过电压现象是谐振电路的特征之一，与基尔霍夫定律并无矛盾。因为根据基尔霍夫定律，L和C两端的电压虽然很大，但它们大小相等、相位相反，达到完全补偿而不需要电源电压再对它们提供能量，电源电压全部供给电路中的电阻R，这个电压绕串联谐振电路一周，其代数和仍然为零，显然符合基尔霍夫定律。