应用戴维南定理的案例分析

（1）应用一 将复杂的有源二端网络化为最简形式

【例2.13】用戴维南定理化简图2-28a所示电路。

解 1）求开路端电压U_oc。在图2-28a所示电路中：

（3+6）I+9-18=0

I=1A

U_oc=U_ab=6I+9=（6×1+9）V=15V

或U_oc=U_ab=-3I+18=（-3×1+18）V=15V

图2-28 例2.13图

2）求等效电阻R_eq。将电路中的电压源短路，得无源二端网络，如图2-28b所示。可得

3）作等效电压源模型。作图时，应注意使等效电源电压的极性与原二端网络开路端电压的极性一致，电路如图2-28c所示。

（2）应用二 计算电路中某一支路的电压或电流

当计算复杂电路中某一支路的电压或电流时，采用戴维南定理比较方便。

【例2.14】用戴维南定理计算图2-28a所示电路中电阻R_L上的电流。

解：1）把电路分为待求支路和有源二端网络两个部分。移开待求支路，得有源二端网络，如图2-29b所示。

图2-29 例2.14图

2）求有源二端网络的开路端电压U_oc因为此时I=0，由图2-29b可得

I₁=（3-2）A=1A(www.xing528.com)

I₂=（2+1）A=3A

U_oc=（1×4+3×2+6）V=16V

3）求等效电阻R_eq将有源二端网络中的电压源短路、电流源开路，可得无源二端网络，如图2-29c所示，则

R_eq=2+4=6Ω

4）画出等效电压源模型 接上待求支路，电路如图2-29d所示。所求电流为

（3）应用三 分析负载获得最大功率的条件

【例2.15】试求上题中负载电阻R_L的功率。若R_L为可调电阻，问R_L何值时获得的功率最大？其最大功率是多少？由此总结出负载获得最大功率的条件。

解：1）利用例2.14的计算结果可得：

P_L=I²R_L=2²×2W=8W

2）若负载R_L是可变电阻，由图2-29d，可得

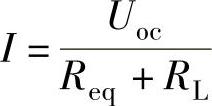
则R_L从网络中所获得的功率

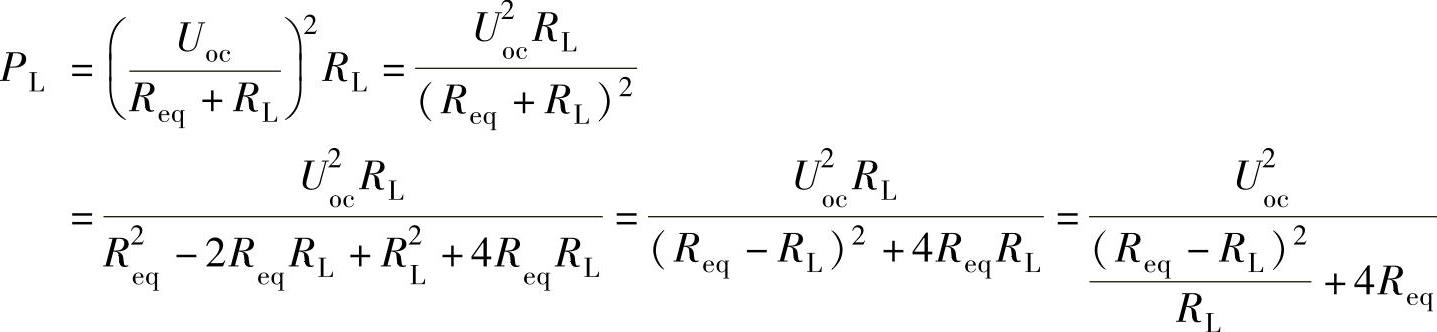
由上式可知，当R_L=R_eq时，功率P₁达到最大值。

最大值为：

综上所述，负载获得最大功率的条件是负载电阻等于等效电源的内阻，即R_L=R_eq。电路的这种工作状态称为电阻匹配。