综合曲线的基本线型是在圆曲线与直线之间加入缓和曲线。如图6.8所示,在直线和圆曲线之间设置缓和曲线,必须向内移动原来的圆曲线,才能使缓和曲线与直线连接。内移圆曲线有两种方法:一是保持圆曲线半径不变,移动圆心;二是圆心不动,缩短半径。在公路测设中,一般采用第一种方法。

图6.8 具有缓和曲线的圆曲线
图中虚线部分为一转角为α、半径为R的圆曲线AB,今欲在两侧插入长度为l 0的缓和曲线。圆曲线的半径不变而将圆心从O 1移至O 2点,圆心内移量为p,p称为曲线内移量。移动后的曲线离切线的距离亦为p,曲线起点沿切线向外侧移动了m,称为切线增长值。将移动后圆曲线的一部分取消,并用弧长为l 0的缓和曲线代替,故缓和曲线大约有一半在原圆曲线范围内,另一半在原直线范围内,缓和曲线的倾角β0即为弧长为l 0的缓和曲线所对的圆心角,称为缓和曲线角(缓和曲线起点切线与终点切线的交角)。
1.缓和曲线常数的计算
缓和曲线的常数包括缓和曲线的倾角β0、圆曲线的内移值P和切线增长值m,根据设计部门确定的缓和曲线长度l 0和圆曲线半径R,其计算公式如下。
(1)缓和曲线角β0
如图6.7所示,在缓和曲线上任意一点i处取一段微分弧长d l,它所对应的圆心角为dβ,根据弧长与半径的关系得

将式(6.11)代入上式后得
![]()
对上式求定积分得i点处的切线偏角为
![]()
因 c=Rl 0
故 ![]()
当l=l 0时,可得(https://www.xing528.com)
![]()
(2)切线增长值m
如图6.9所示,m=x 0-b=x 0-R sinβ0
因 ![]()
故 ![]()
用级数展开![]() 并略去高次项得
并略去高次项得

图6.9 曲线移动量和切线增长值
![]()
(3)曲线内移量p
从图6.9中可知,p=R cosβ0+y 0-R=R(cosβ0-1)+y 0
因![]() ,用级数展开cosβ0并略去高次项,整理后得
,用级数展开cosβ0并略去高次项,整理后得

2.有缓和曲线的圆曲线要素计算
在计算出缓和曲线的倾角β0、圆曲线的移动量p和切线增长值m后,就可计算具有缓和曲线的圆曲线要素
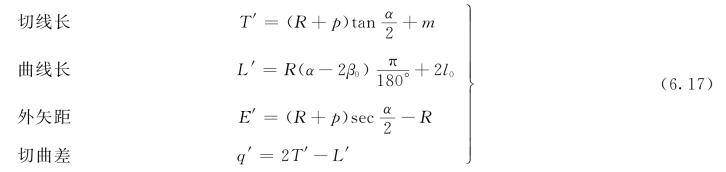
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




