数字测图中地物点平面位置精度的分析

（1）定向误差对地物点平面位置的影响m定

式中　D——测站点到地物点的平距；

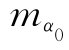——定向方位角中误差；

ρ——206265″。

设测站点坐标为（x 0，y 0），定向点坐标为（x 1，y 1），测定向方位角α0为

对式（2.3）微分得

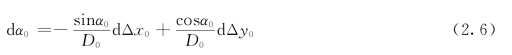
式中　D 0——测站点到定向点的平距。

将式（2.4）转化为中误差形式

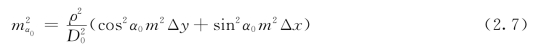
式中，设两个图根点之间的相对中误差为m xy，且

则

（2）对中误差对地物点平面位置的影响m中

对中误差包括测站对中误差和定向对中误差，它通过对测站的影响而影响地物点平面位置。(www.xing528.com)

根据对中误差对测角的影响可推求得

式中　m 1——仪器上光学对中器的对中误差，一般不超过3mm；

D、D 0含义同前。

（3）观测误差对地物点平面位置的影响m测

数字测图时是根据测量的距离和角度直接解算地物点坐标，观测误差主要包括测距误差和测角误差两部分，根据误差传播理论，推出观测误差对地物点平面位置的影响m测为（不考虑测站点起始误差）

式中　A——测距仪固定误差；

B——测距仪比例误差；

mβ——测角中误差。

（4）棱镜中心与待测地物点不重合对地物点平面位置的影响m重

此项误差的影响可控制在2.0cm之内，取m重＝2cm。

一般情况下D/D2.0cm，分别代入式 0≤1.5，两个图根点之间的相对中误差mxy取（2.9）、式（2.10），得m定＝2.1cm，m中＝0.5cm。

根据不同的测距测角精度和观测平距，由式（2.11）计算出m测，并与上述的m定＝2.1cm，m中＝0.5cm、m重＝2cm一起代入式（2.1），计算所得的地物点平面位置中误差列于表2.1中。

表2.1　数字测图地物点（实物）平面位置中误差

由表2.1可以看出，即使用最低精度的仪器（测距精度5mm＋10×10－6D，测角精度10″），在观测平距不超过400m时，所测地物点相对于邻近图根点的平面位置中误差可保证在5cm以内（实施），这大大高于模拟法测图的精度，充分体现了数字法测图在精度方面的优势。另外，这也是精度要求较高的城镇地籍测量、房产测量、房产测量、地下管网测量等目前均要用数字法测图的原因之一。