结构设计计算书的优化

一、剪力墙、框架及连梁的刚度计算

（一）框架的等效剪切刚度CF1

1.梁的线刚度计算

梁的线刚度计算见表5-4-1。

表5-4-1　梁线刚度

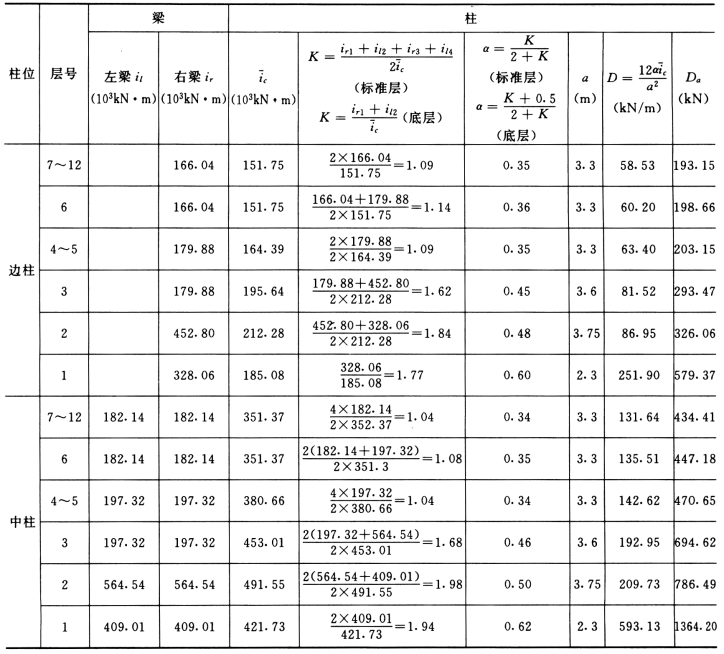
2.柱的线刚度计算

柱的线刚度计算见表5-4-2。

表5-4-2　柱线刚度

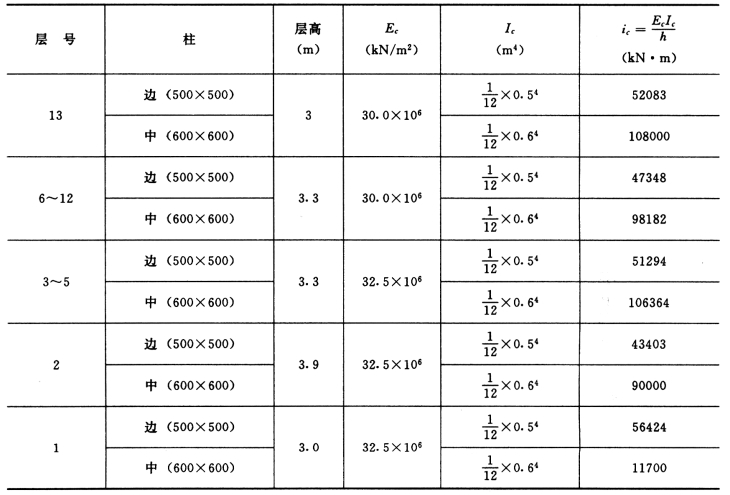
3.框架柱侧移刚度

框架柱侧移刚度（D）计算见表5-4-3。

表5-4-3　框架柱侧向刚度（D）值计算

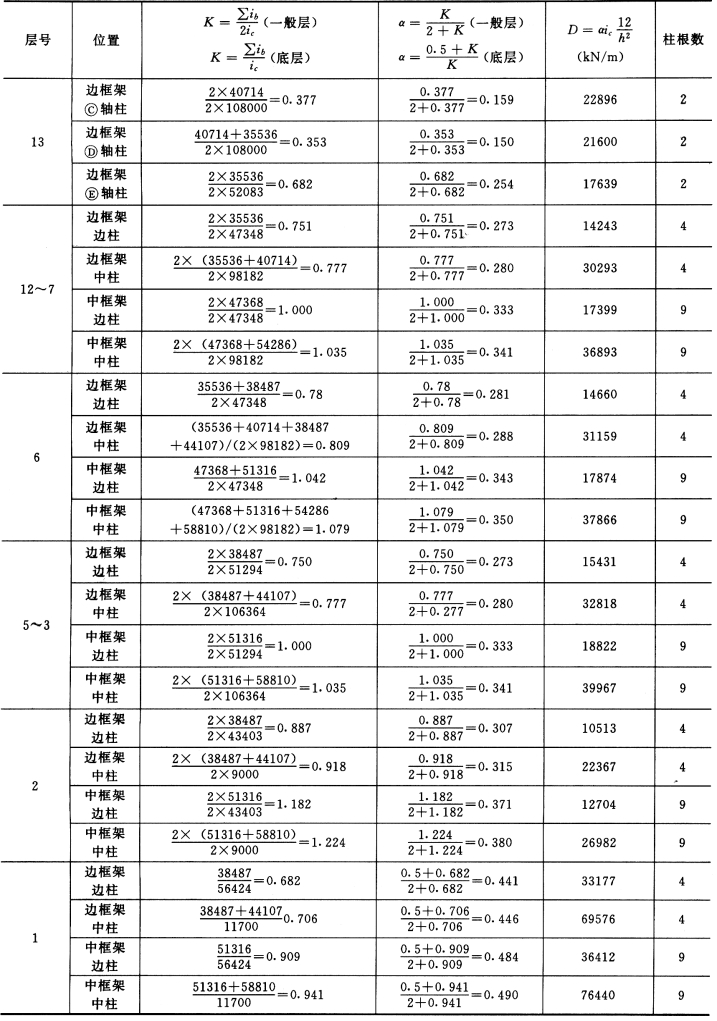
对于高度小于50m 且高宽比小于4 的建筑物，仅考虑梁柱弯曲变形引起的柱侧移刚度，忽略柱的轴向变形。与剪力墙相连的边柱作为剪力墙的翼缘，计入剪力墙的刚度，不作为框架柱处理。

第13层总D值：D13=ΣD=2×（22896+21600+17639）=124270 kN/m

等效剪切刚度：Cf13=ΣDh=124270×3=372810 kN=37.28×104 kN

同理：

Cf12=Cf11=Cf10=Cf9=Cf8=Cf7=220.02×104 kN

Cf6=226.03×104 kN，Cf5=Cf4=Cf3=238.29×104 kN

Cf2=190.59×104 kN，Cf1=428.00×104 kN

框架剪切刚度：

（二）剪力墙的等效刚度EIeq

1.剪力墙W—1 的刚度计算

剪力墙截面见图5-4-1，剪力墙厚250mm，1～5 层混凝土C40，6～12 层混凝土C30

有效翼缘宽度：

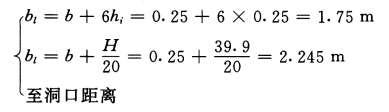
取小值，bi=1.75m。

墙肢面积：Aw=0.62+0.52+1.325×0.25+5.15×0.25=2.229m2

墙肢形心：

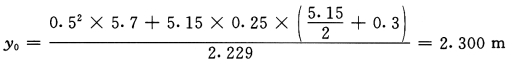
墙肢惯性矩：

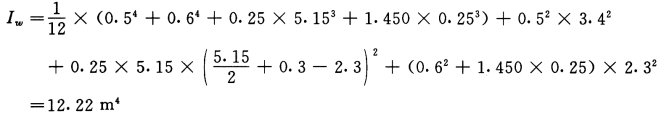
图5-4-1　W—1 截面

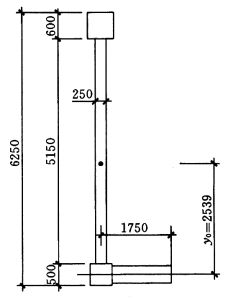
图5-4-2　W—2 截面

截面不均匀系数μ=1.73，等效刚度为

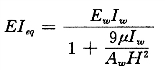
1～5 层：

ΣEwIw=12.22×3.25×107=396.5×106 kN·m2

ΣEIeq=376.32×106 kN·m2

6～12 层：

ΣEwIw=12.22×3.25×107=396.5×106 kN·m2

ΣEIeq=347.94×106 kN·m2

W—1 等效刚度按层高加权平均得：

EIeq1=359.89×106 kN·m2

2.剪力墙W—2 的刚度计算

剪力墙截面见图5-4-2，与W—1 计算过程相同。

Aw=2.241m2，y0=2.559m2，Iw1=13.30m4，截面不均匀系数μ=1.735，则

1～5 层：

ΣEwIw=432.3×106 kN·m2

ΣEIeq=408.32×106 kN·m2

6～12 层：

ΣEwIw=399.00 X 106 kN·m2

ΣEIeq=376.87×106 kN·m2

W—2 等效刚度：

EIeq2=390.11×106 kN·m2

3.横向剪力墙总等效刚度

横向剪力墙总等效刚度为

EIeq=（2×359.89+390.11）×106=1109.89×106 kN·m2

（三）连梁约束刚度CB

截面0.25m×0.40m，1～5 层混凝土为C40，6～12 层为C30。一端有刚域，如图5-4-3所示。

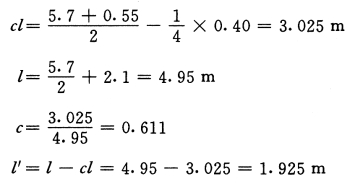
图5-4-3　框架剪力墙连梁刚域图

（应算至墙肢形心，考虑与W—1、W—2 相连连梁的墙肢形心与墙体中心相差不远，本题为简化计算统一算至墙肢中心。）

面积：

A=0.25×0.40=0.1m2

惯性矩：

查表得剪应力不均匀系数：

μ=2.06

考虑剪切变形：

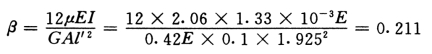
连梁约束弯矩：

6～12 层：m12=1.09×106 kN·m

连梁等效剪切刚度：

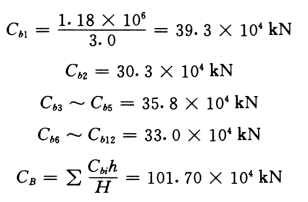
（四）壁式框架柱剪切刚度CF2

1.WF—1 的类型判别

（1）墙肢惯性矩Ij、墙肢截面积Aj 及组合截面惯性矩I。不考虑墙肢翼缘作用时，WF—1的截面尺寸如图5-4-4所示。

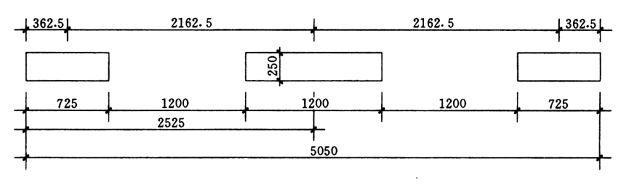
图5-4-4　WF—1 不考虑翼缘作用截面图

墙肢：

I1=0.0079m4

I2=0.036m4

I3=0.0079m4

ΣIj=0.0518m4

A1=0.181m2

A2=0.3m2

A3=0.181m2

ΣAj=0.662m2

组合截面：I=0.0518+0.181（2.525-0.3625）2×2=1.745m4

（2）连梁折算惯性矩。连梁折算惯性矩Ibj0、截面积Abj、计算跨度lj 及折算惯性矩Ibj（见表5-4-4）。

表5-4-4　WF—1 连梁折算惯性矩

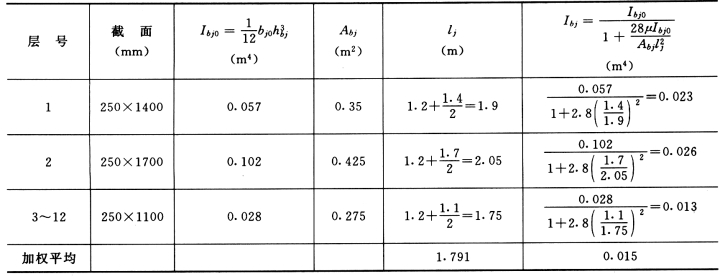
（3）整体系数α及。第1 列连梁：

第1 列洞口两侧墙肢轴线距离：a1=2.1625m

高度加权平均：h=（3.0×3.0+3.9×3.9+3.3×3.3×10）/39.9=3.34

整体系数：

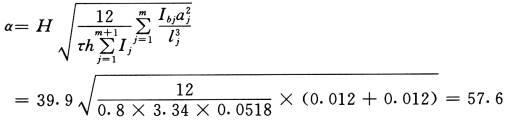
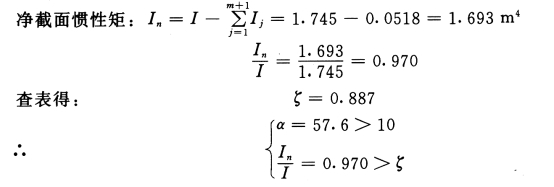
判断为壁式框架。

当墙肢考虑翼缘时，仍判断为壁式框架。本算例按不考虑墙肢翼缘作用来计算壁式框架。

2.壁式框架WF—1 的刚域长度计算

以底层为例。

壁梁刚域长度：

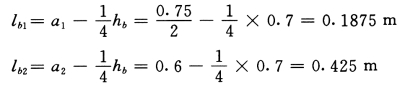
边柱壁柱刚域长度：

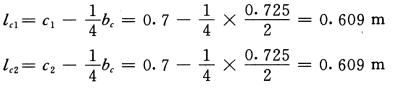
WF—1 的尺寸及各杆件的刚域长度详见图5-4-5（杆件的宽度bb 均为250mm）。

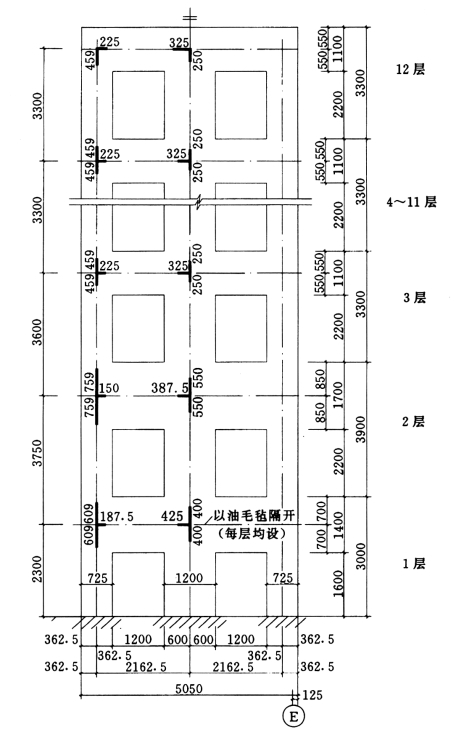
图5-4-5　WF—1 的立面尺寸及刚域长度

3.梁和柱考虑刚域及剪切变形影响的折算线刚度

（1）梁柱的惯性矩。因WF—1 的梁在净跨范围内由两根高度相等的梁组成，所以双层梁的惯性矩等于两单梁惯性矩之和。

（2）壁梁和壁柱的折算线刚度（计算简图见图5-4-6）。WF—1的梁和柱折算线刚度，分别列于表5-4-5和表5-4-6中。

图5-4-6

梁柱均为矩形截面：

表5-4-5　壁梁杆端转动折算线刚度

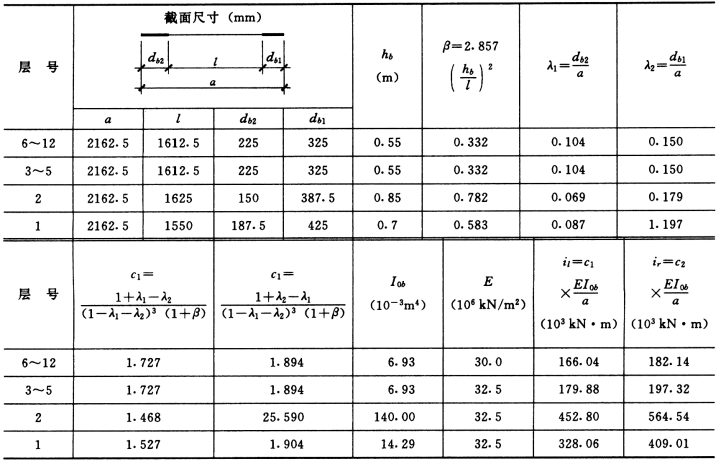
表5-4-6　壁柱杆端转动折算线刚度i1、i2 及侧移折算线刚度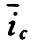

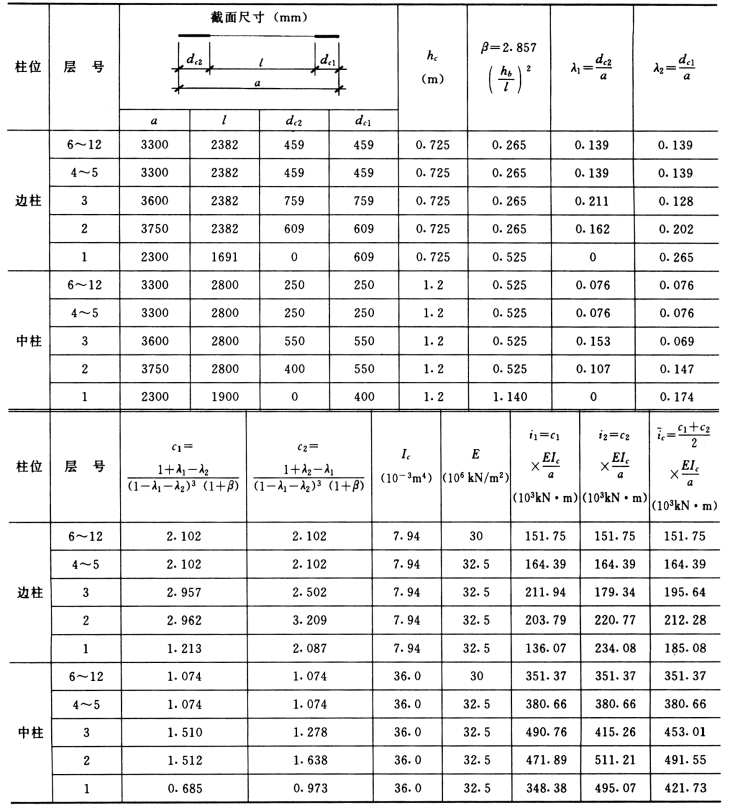
考虑剪切变形影响的附加系数β：

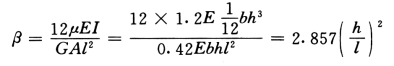
壁梁折算线刚度：

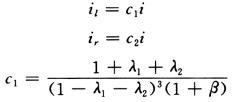
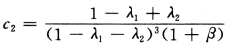
壁柱折算线刚度：

WF—1 各杆的折算线刚度见图5-4-7。

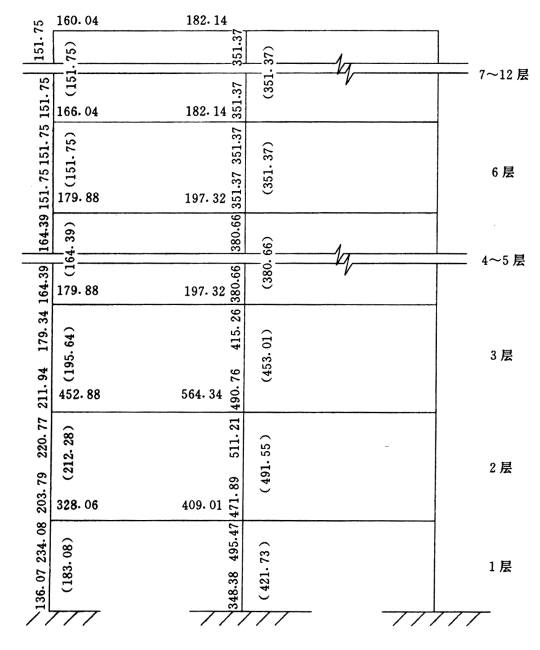
图5-4-7　WF—1 杆件的杆端转动折算线刚度及柱的侧移折算线刚度（括号内数字）（单位：103kN）

（3）壁柱的侧移刚度D（见表5-4-7）及壁式框架剪切刚度CF2。

壁式框架柱剪切刚度：

边柱：ΣDa=2669.29×103 kN

中柱：ΣDa=7043.72×103 kN

壁式框架总剪切刚度：

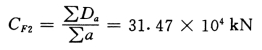
总框架剪切刚度：

CF=CF1+CF2=237.81+31.47=269.28 kN

表5-4-7　壁柱的侧移刚度D 值和Da 值

（五）主体结构刚度特征值

主体结构刚度特征值（不考虑连梁刚度折减，壁式框架剪切刚度计入框架中）λ为

二、水平地震作用效应分析

（一）水平地震荷载计算

对高度不超过40m 以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，可采用底部剪力法。

1.结构基本自振周期

荷载计算从略。

GE=ΣGi=2046.5+9522.4+8296.8×9+8371.2+8251.0=102862.3 kN

Geq=0.85GE=0.85×102862.3=87433 kN

假想把集中在各层楼面处的重力荷载代表值Gi 视作水平荷载来计算结构顶点侧移uT，并进一步简化为均布荷载q，则

在均布荷载作用下，由总剪力墙单独承受水平荷载时的顶点位移为

在顶点处，Z=39.9m，由ζ==1，λ=2.30查表得框—剪结构在均布荷载作用下的顶点位移系数为0.341，则

uT=Δm×0.341=0.736×0.341=0.251m

对质量和刚度沿高度均匀的框—剪结构，结构自振周期由顶点侧移确定，可按下式计算：

2.总水平地震作用

该场地土Ⅱ类，场地特征周期Tg=0.3s，αmax=0.08，则

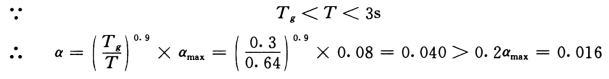
主体结构底部剪力标准值为

FEK=αGeq=0.040×87433=3497.3 kN

3.各楼层质点的水平地震作用

∴顶部附加地震作用系数：

δn=0.08T1+0.07=0.08×0.64+0.07=0.1212

附加顶端集中荷载：ΔFn=δnFEK=0.1212×3497.3=423.9 kN

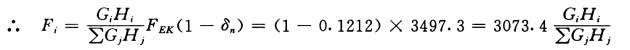
Fi 计算结果见表5-4-8。

表5-4-8　各楼层质点的水平地震作用

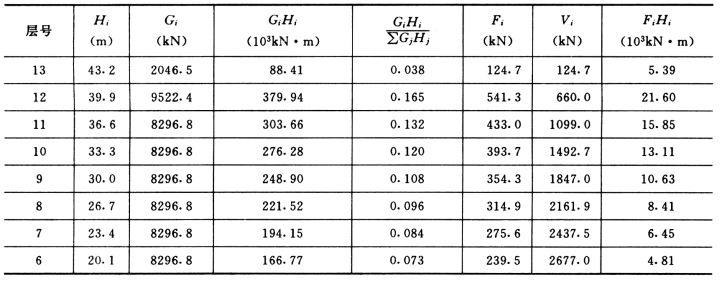
续表

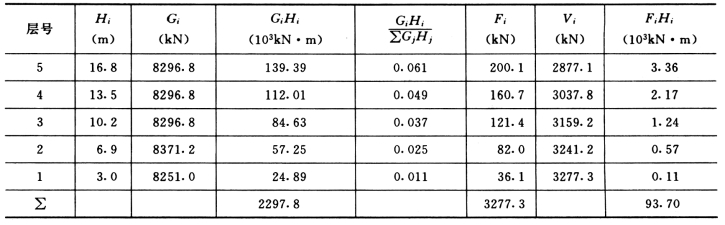
为后续计算方便，将各楼层质点i 的水平地震作用Fi 和顶点附加水平地震作用ΔFn，按基底弯矩和基底剪力相等原则折算为倒三角形连续分布荷载和顶点集中荷载，如图5-4-8所示。

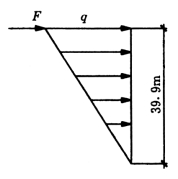
图5-4-8　荷载形式

由基底弯矩：

基底剪力：

得

q=140.2 kN/m

F=700.9 kN

（二）框架—剪力墙协同工作计算

1.框架—剪力墙协同工作计算简图

框架—剪力墙协同工作计算简图见图5-4-9。

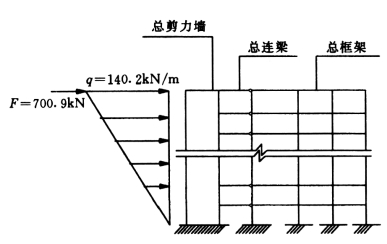
图5-4-9　框剪协同工作计算简图

建筑物横向所有框架、所有剪力墙和所有连梁各自综合在一起，分别形成总框架、总剪力墙和总连梁。

2.结构顶点位移及层间位移验算

考虑连梁塑性调幅，其刚度折减系数取为0.55，重新计算λ值：

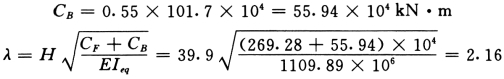
结构顶点位移为

倒三角形荷载：

顶点集中荷载：

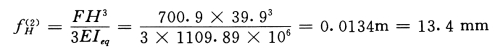
查图表可计算出各楼层标高处的位移，结果见表5-4-9。

表5-4-9　位移计算

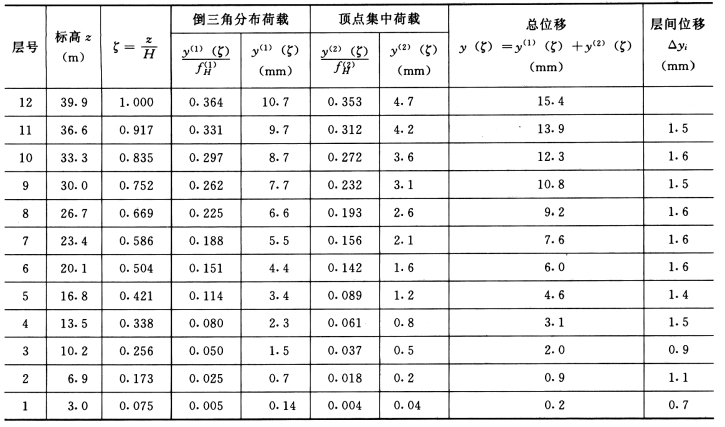
由表5-4-9可知：

层间位移：

顶点位移：

3.总剪力墙、总框架和总连梁的内力

（1）按折算倒三角形荷载计算悬臂剪力V（1）（ζ）及其基底剪力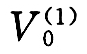和基底弯矩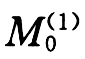；按折算顶端集中荷载计算悬臂剪力V（2）（ζ）及其基底剪力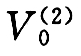和基底弯矩：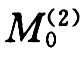

总悬臂剪力：

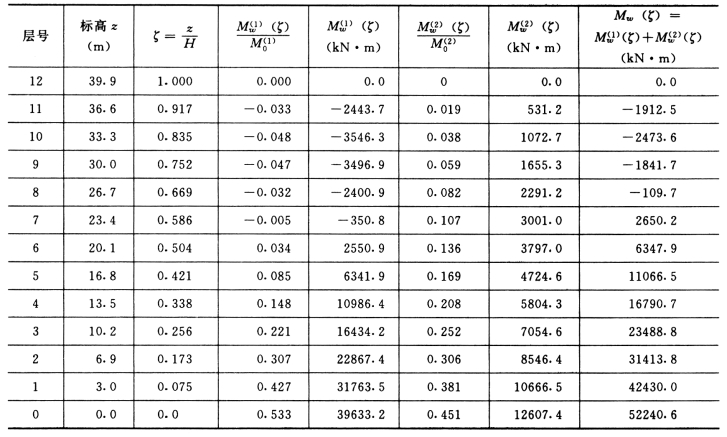
（2）由λ=2.16 查图表计算各楼层标高处总剪力墙弯矩系数，从而求得总剪力墙弯矩，计算见表5-4-10。

表5-4-10　总剪力墙弯矩计算表

（3）查图表得各楼层中间标高处剪力系数，从而得V'w（ζ），计算过程及结果见表5-4-11。

表5-4-11　总剪力墙Vw'值计算表

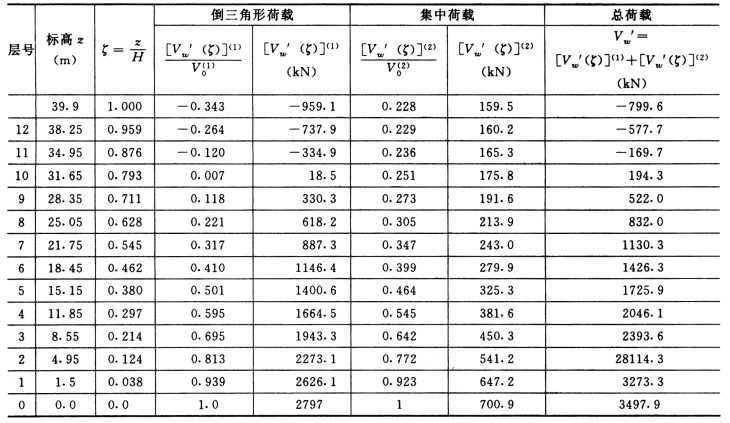
（4）总剪力墙剪力Vw（ζ）、总框架剪力Vf（ζ）和总连梁线约束弯矩m（ζ）之和为

倒三角形荷载：

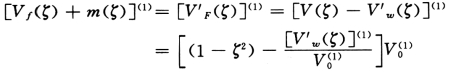
顶点集中荷载：

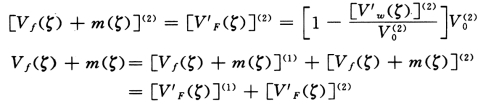
总框架剪力：

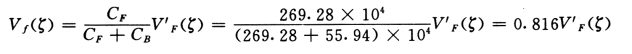
总连梁线约束弯矩：

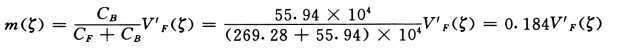
总剪力墙剪力：

Vw（ζ）=V'w（ζ）+m（ζ）

计算过程及结果见表5-4-12。

表5-4-12　总连梁线约束弯距m（ζ）、总框架剪力Vf（ζ）和总剪力墙剪力Vw（ζ）

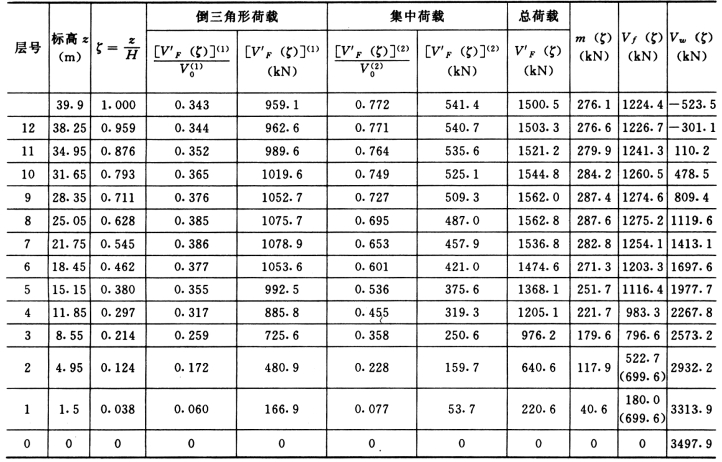
注 0.2V0=0.2（27970+700.9）=699.6kN，1.5Vf，max=1.5×1275.2=1913 kN，取1～2层为699.6kN（表中括号内数字）。

（5）总框架剪力的调整：对总框架剪力Vf＜0.2V0 的楼层，楼层Vf 取Vf 和0.2V0 中较小值。各层框架总剪力调整后，按调整前后的比例放大各柱和梁的剪力和端部弯矩；柱轴力不放大。

总剪力墙在结构底部承担地震弯矩×100%=51.0%＞50%

因此，框架抗震等级为三级，剪力墙抗震等级为二级。

（三）连梁内力计算

1～12 层计算简图如图5-4-10所示。

图5-4-10　一端刚域连梁计算简图

连梁250mm×400mm，l=4.95m。

连梁刚域长度cl=3.025m，c=0.611，计算长度l'=1.925m。

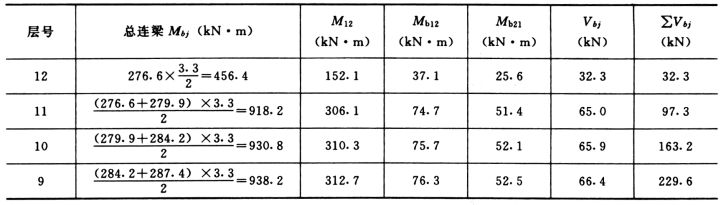
各层连梁总约束弯矩：

每根连梁的约束弯矩：

M12=Mbj/3

1～5 层连梁计算弯矩：

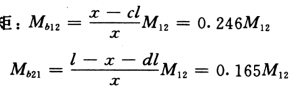
连梁计算剪力：

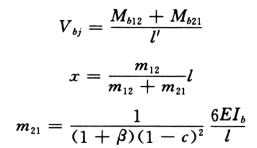
式中：m12、β计算分别见连梁的约束刚度部分。

同理，6～12 层：

Mb12=0.244M12

Mb21=0.168M12

连梁内力计算结果见表5-4-13（单根连梁）。

表5-4-13　地震作用下连梁内力

续表

（四）单片剪力墙的内力

水平荷载下剪力墙的内力计算，按各片剪力墙的等效刚度进行分配，由此计算单片剪力墙的内力。

H=39.9m＜50m，H/B=39.9/13.5=2.96＜4，由《钢筋混凝土高层建筑结构设计与施工规程》可知，仅考虑弯曲变形影响，不考虑柱和墙肢的轴向变形。

考虑与连梁连接的剪力墙受连梁弯矩、剪力的影响，第j层第i 个墙肢的弯矩和剪力分别为

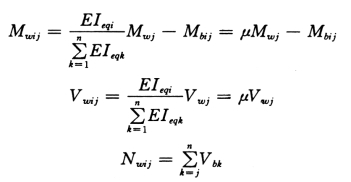
其中，W—1分配系数μ=0.254，W—2分配系数μ=0.352。

计算结果见表5-4-14。

（五）框架内力计算

1.框架地震剪力Vf 在各框架柱间的分配

取⑨轴一榀横向框架。

（1）第j层第i 柱所分配剪力：

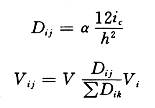
（2）框架柱反弯点位置：各层柱反弯点高度比y根据式（3-4-10）计算，结果见表5-4-15。

表5-4-14　地震作用单片剪力墙内力

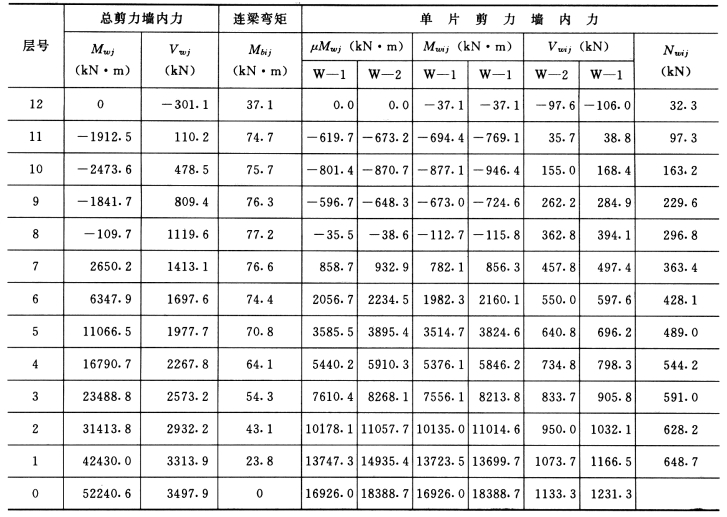
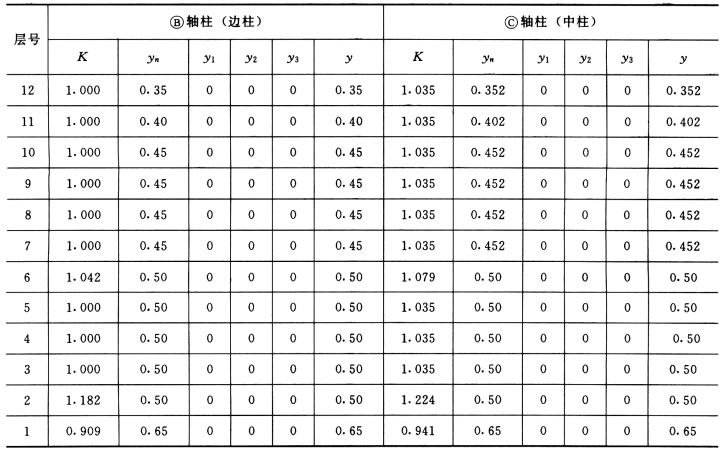
表5-4-15　框架柱及反弯点位置

（3）框架梁柱节点弯矩分配（见图5-4-11）。

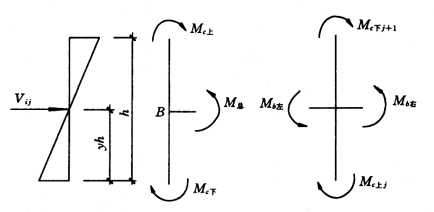
图5-4-11　框架节点弯矩分配

计算结果见表5-4-16。

表5-4-16　框架梁柱弯矩

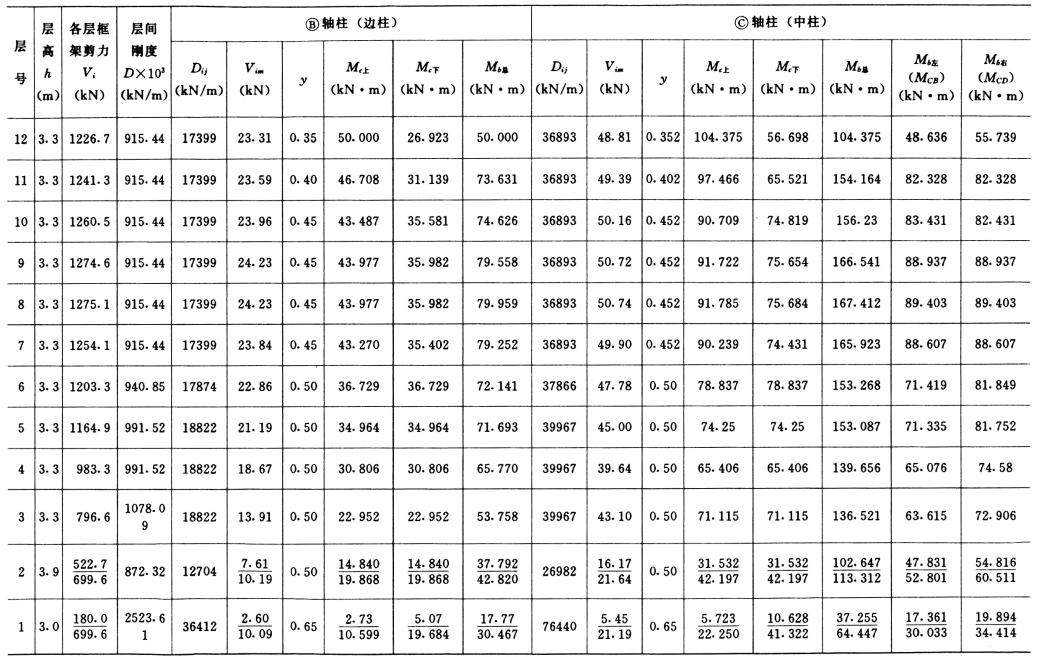
注 表内横线以上数字为实际计算所得数字，用于计算柱轴力；横线以下为调整放大后所得数字，用于计算梁柱弯矩和剪力。

2.框架柱轴力与框架梁剪力计算

（1）框架梁剪力：

梁BC：

梁CD：

梁DE：

其中：l=5.7m，l'=2.1m。

（2）框架柱轴力：

NCjB=VBCj

NCjE=VDEj

N=Σ（V右梁-V左梁）

NCjC=Σ（VDEj-VBCj）

NCjD=Σ（VDEj-VCDj）

梁柱计算结果见表5-4-17。

表5-4-17　⑨轴框架柱轴力与梁端剪力

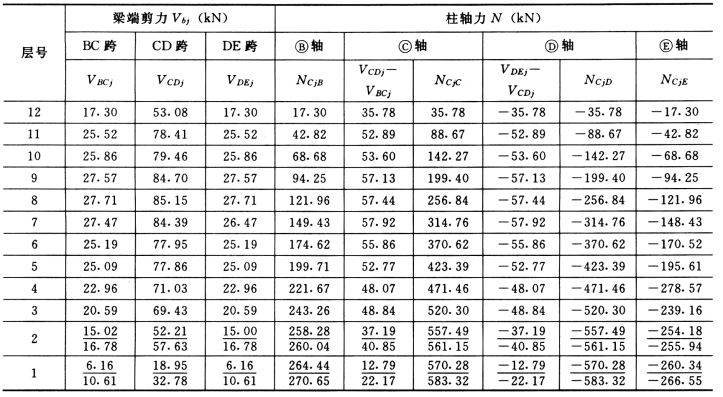
注 横线以上数字为未经放大的数字，计算轴力时取用该项数值。

三、竖向荷载作用下框架和剪力墙内力计算

（一）框架内力计算

以⑨轴横向框架为例。

1.荷载及计算简图

（1）屋面荷载：

（2）楼面荷载：

（3）楼面荷载分配为等效均布荷载（如图5-4-12所示）：

图5-4-12

短向分配荷载：

长向分配荷载：

（4）横向框架梁上线荷载：

1）BC 跨（DE 跨）：

2）CD 跨：

（5）横向框架柱上集中荷载：

1）⑧轴次梁L—1 线荷载：

2）Ⓑ轴次梁KL-C 荷载：

3）Ⓒ轴次梁KL—C 荷载：

4）边柱集中荷载：

5）中柱集中荷载：

框架竖向荷载如图5-4-13所示。

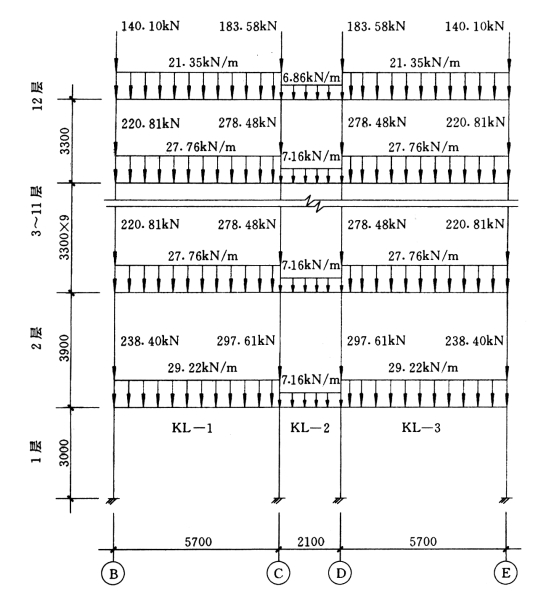
图5-4-13　⑨轴框架竖向荷载

2.框架弯矩计算

在竖向荷载作用下框架内力采用分层法进行简化计算，此时每层框架连同上下层柱组成基本计算单元，竖向荷载产生的梁固端弯矩只在本层内进行弯矩分配，单元之间不再传递。梁的弯矩取分配后的数值；柱端弯矩取相邻两层单元对应柱端弯矩之和。

（1）梁的固端弯矩（见表5-4-18）：

表5-4-18　⑨轴框架梁固端弯矩计算表（KN·m）

（2）柱的线刚度（见表5-4-19）：(www.xing528.com)

表5-4-19　⑨轴框架线刚度

（3）梁的线刚度：

K L—1

（b×h=0.25m×0.6m）

6～11 层：

ib=47368 kN·m

1～5 层：

ib=51316 kN·m

K L—2

（b×h=0.25m×0.45m）

6～11 层：

ib=54286 kN·m

1～5 层：

ib=58810 kN·m

（4）分配系数：考虑框架对称性，取半框架进行计算。半框架的梁柱线刚度如图5-4-14所示。切断横梁线刚度为原来的2 倍，分配系数按与节点连接的各杆的转动刚度比值计算。

图5-4-14　⑨轴半框架梁柱线刚度示意（kN·m）

【例】 B 柱顶层节点。

（5）传递系数：底层柱传递系数为1/2，其余各层柱传递系数为1/3；梁远端固定传递系数为1/2，远端滑动铰支座传递系数为-1。

（6）弯矩分配（分配过程见图5-5-15）。

图5-4-15　⑨轴竖向荷载弯矩分配图（kN·m）

（7）节点不平衡弯矩的再分配：由于柱端弯矩按1/3 传递系数传递到远端（底层按1/2 传递系数），柱端弯矩取相邻两层单元对应柱端弯矩之和，此时原来已经平衡的结点弯矩由于加入了新的弯矩而不再平衡，应将不平衡弯矩再分配，计算过程见表5-4-20。

表5-4-20　⑨轴结点不平衡弯矩配计算表

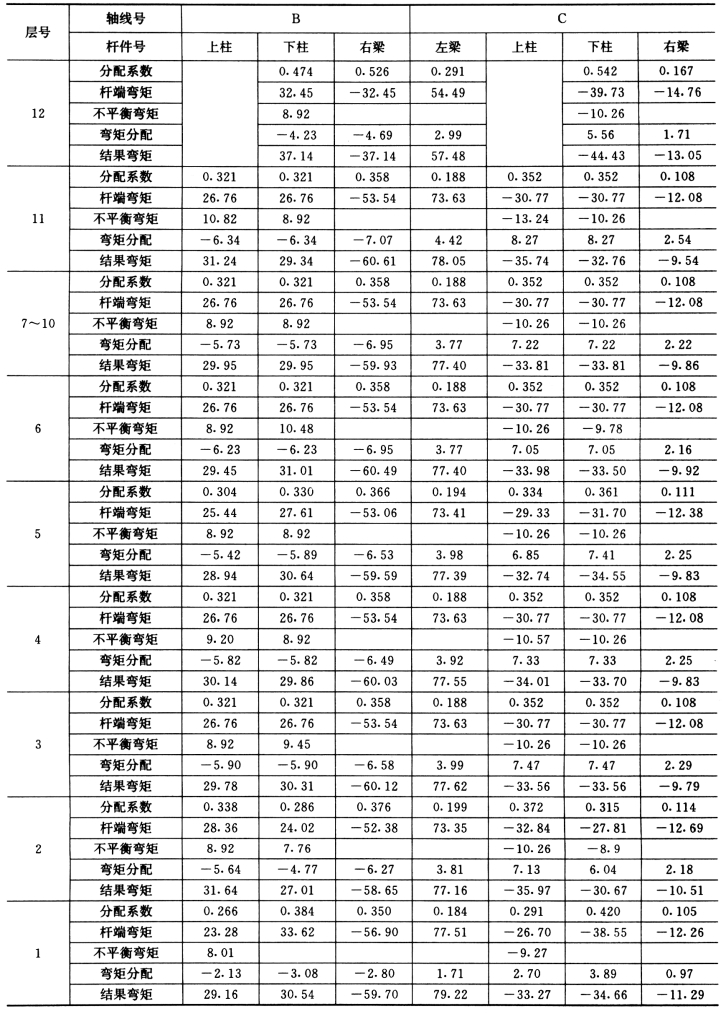
用分层法进行近似计算的梁柱最终弯矩值见图5-4-16。

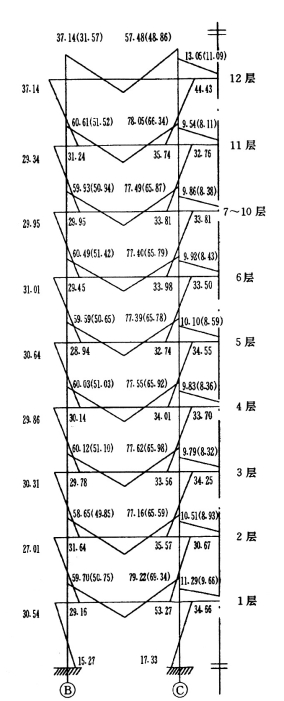
图5-4-16　分层法计算的⑨轴梁柱弯矩

在竖向荷载作用下，对梁端负弯矩进行调幅，调幅系数取0.85。

3.梁剪力及柱轴力计算

（1）梁端剪力：

（2）柱轴力：

N=V（梁端剪力）+P（节点集中力及柱自重）

竖向荷载作用下梁端剪力及柱轴力计算见表5-4-21。

表5-4-21　竖向荷载作用下梁端剪力及柱轴力

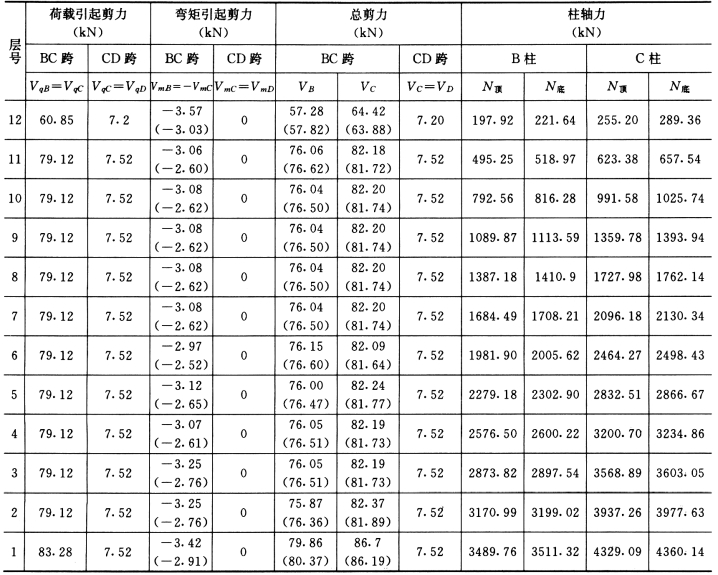
注 括号内为调幅后的剪力值。

（二）剪力墙内力计算

1.连梁传递的荷载

连梁KL—4 传递给剪力墙的竖向荷载使剪力墙产生轴力Ni 和弯矩Mi，见图5-4-17。

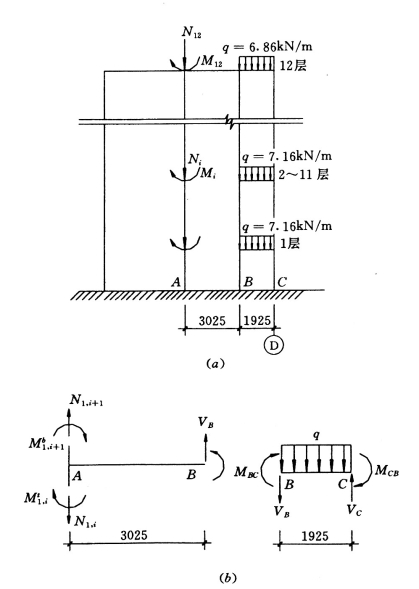
图5-4-17　⑩轴剪力墙受连梁传递荷载作用

（a）剪力墙荷载图；（b）剪力墙计算简图

剪力墙各层弯矩M1i按下式计算：

M1i=MBC，i+3.025VB，i（kN·m）

M1i应按剪力墙线刚度分配给上层剪力墙及下层剪力墙：

各层轴力则为

其中MBC，i及VB，i由⑩轴框架内力计算而得。⑩轴框架在竖向荷载作用下计算方法同⑨轴框架，其计算简图见图5-4-18。

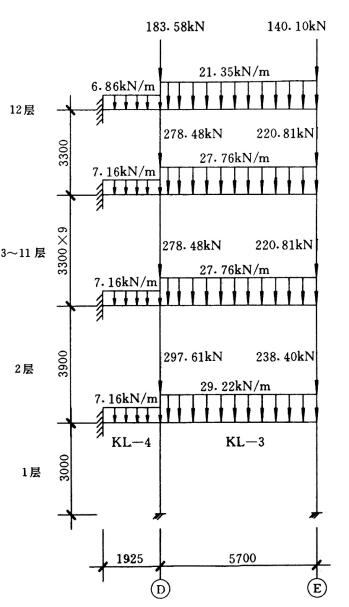
图5-4-18　⑩轴框架竖向荷载

⑩轴框架柱线刚度同⑨轴，见表5-4-18。

⑩轴框架梁线刚度：

K L—3（250mm×600mm）：

6～12层：

ib=47368 kN·m

1～5 层：

ib=51316 kN·m

⑩轴框架竖向荷载弯矩分配图见图5-4-19。

图5-4-19　⑩轴框架弯矩分配图

⑩轴框架竖向荷载结点不平衡弯矩分配见表5-4-22。

表5-4-22　⑩轴框架结点不平衡弯矩分配计算表（kN·m）

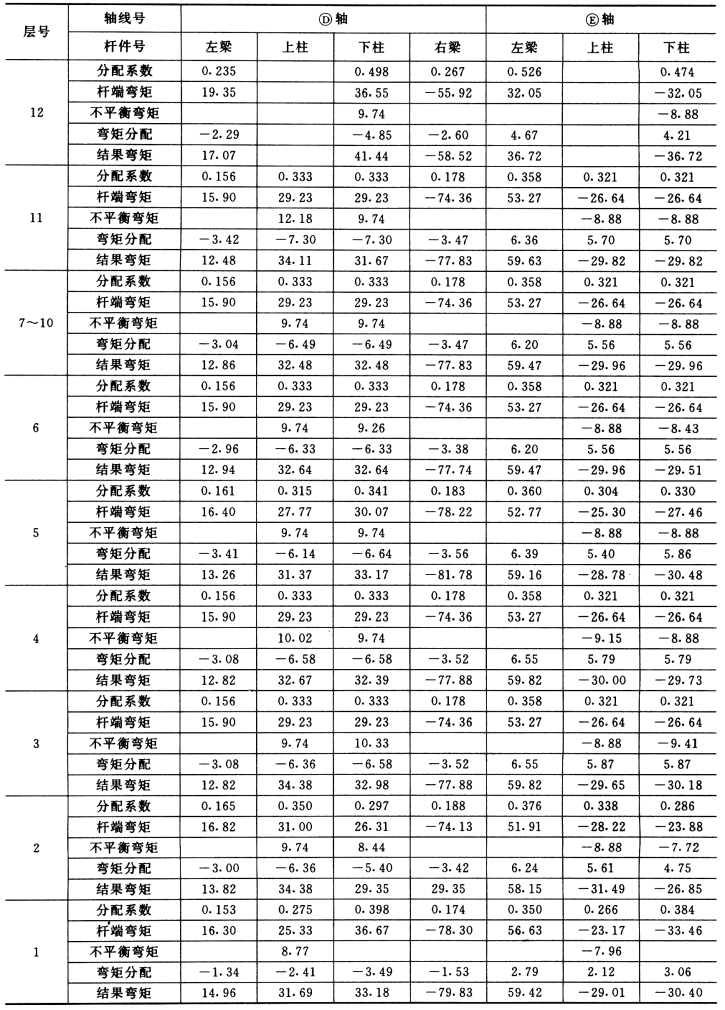
KL—4在竖向荷载下的最终弯矩图如图5-4-17（b）中BC梁所示，由此得KL—4在竖向荷载作用下的剪力VB，j。

如12 层：

MBC=6.40 kN·m

MCB=17.07 kN·m

2.楼板传来的竖向荷载

楼板传给剪力墙的竖向荷载如图5-4-20所示，集中荷载为楼板、Ⓒ轴纵梁、剪力墙传至柱，它使剪力墙产生轴力N2i和弯矩M2i。

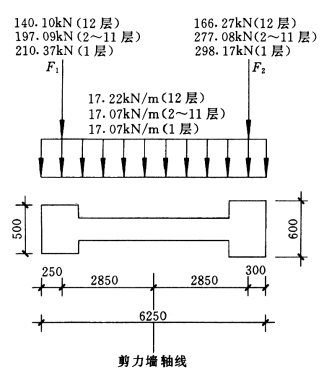
图5-4-20　⑩轴剪力墙受楼板传来竖向荷载

轴力N2i：

12 层：

N2=17.22×6.25=107.63 kN

1～11 层：

N2=106.69 kN

弯矩M2i：

12 层：

M2=（166.27-140.10）×2.85

=74.58 kN·m

2～11 层：

M2=227.97 kN·m

1 层：

M2=250.23 kN·m

M2i应按剪力墙线刚度分配给上层剪力墙及下层剪力墙：

3.墙自重

墙自重按每层重量计。

3～12 层：

N3=（0.5×0.5+0.6×0.6+0.25×5.15）×3.3×25×1.15=180.0 kN

2 层：

N3=212.8 kN

1 层：

N3=163.7 kN

4.竖向荷载作用下产生的剪力VG

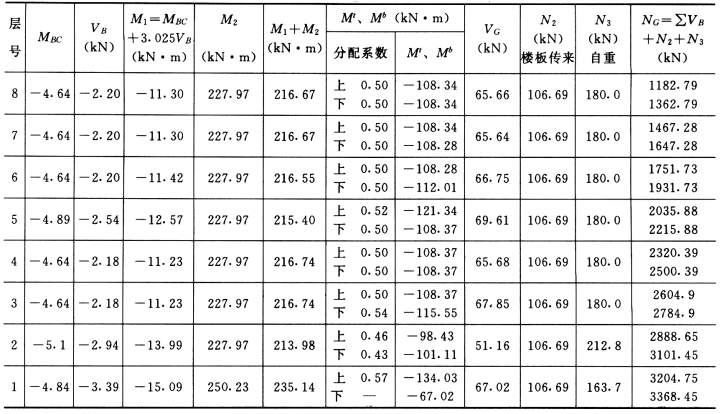
竖向荷载作用下⑩轴剪力墙W—1 的弯矩、轴力及剪力见表5-4-23。

表5-4-23　竖向荷载作用下剪力墙⑩轴W—1 的内力计算

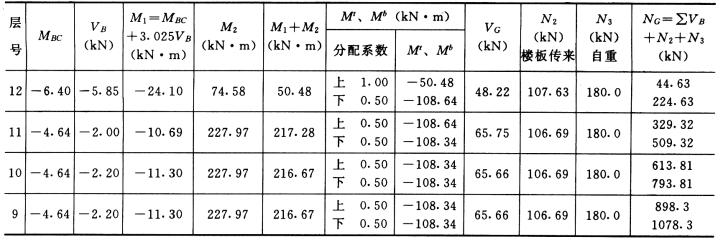
续表

四、荷载效应组合

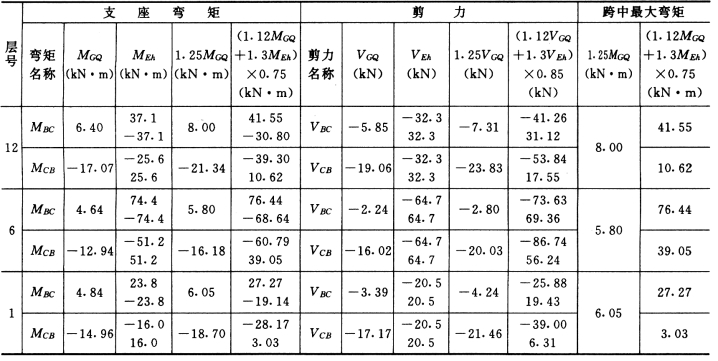
本节内容仅列出⑨轴1、6、12 层梁柱的内力组合过程，其余层计算方法相同，不再赘述。

在只考虑竖向荷载情况下，按规定应分别计算出在恒载和活载作用下结构的内力，然后乘上各自的分项系数以获得恒载和活载组合时的内力，在本例中，考虑了活载占全部竖向荷载的实际比例，当取竖向荷载的综合分项系数γGQ=1.25 时，其计算结果十分相近，即

1.2CGGK+1.4CQQK≈1.25（CGGK+CQQK）=1.25CGQGGQ

为计算方便，本例仅计算出全部竖向荷载（恒载+活载）作用下结构的内力，当乘以综合分项系数γGQ=1.25 时，即为只考虑竖向荷载的组合结果。

在竖向荷载作用下，先考虑梁端负弯矩的调幅，然后再计算剪力和跨中弯矩，进行内力组合。

考虑竖向荷载代表值取恒载100%、活载50%，故本例竖向荷载代表值约占总重力荷载的93%，当与地震作用组合时，取γGCGGE≈1.2γG×0.93CGQGGQ=1.12CGQGGQ。

钢筋混凝土高层建筑结构构件的承载能力按下列公式验算：

非抗震设计：

γ0S≤R

抗震设计：

S≤R/γRE

为了计算比较，本例在内力组合以获得荷载效应组合设计值S 的同时，乘上结构重要性系数和抗震能力调整系数，即对抗震设计采用下列表达式：

γRES≤ R

（一）梁的支座弯矩和剪力

考虑到水平地震作用可自左向右和自右向左作用，分别引起大小相等而方向相反的支座弯矩和剪力。当竖向荷载效应与水平地震作用效应组合时，支座弯矩和剪力按下列各式组合：

支座负弯矩：

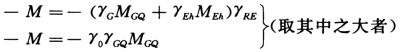
支座正弯矩：

+M=（γEhMEh-γGMGQ）γRE

梁端剪力：

V=（γEhVEh+γGVGQ）γRE

V=γ0γGQVGQ

支座正负弯矩、梁端剪力的组合结果见表5-4-24。

表5-4-24　框架梁内力组合

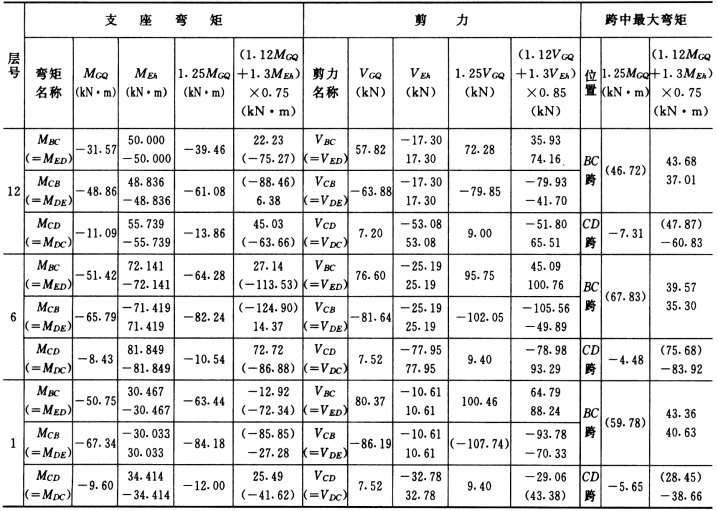
注 1.跨中最大正弯矩、支座最大负弯矩均按竖向荷载支座负弯矩调幅后，并跟地震作用组合后的端弯矩求得。
2.截面设计时取用括号内数值。

（二）梁的跨中最大弯矩

跨中正弯矩：

式中：Mmax为梁跨范围内γGMGQ+γEhMEh的最大正值；MGQ，max为竖向荷载（恒载和楼面活载）标准值引起的梁跨范围内最大正弯矩。

现以⑨轴六层KL—1为例计算梁的跨中最大正弯矩。

1.仅考虑竖向荷载

如图5-4-21所示，仅考虑竖向荷载：剪力为零值点距B 点距离为x，则76.60=27.76x，x=2.759m，此截面处跨中弯矩最大，即

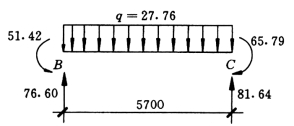
图5-4-21　六层KL—1 竖向荷载

取γ0=1，γGQ=1.25，则

M=γ0γGQMGQ，max=1×1.25×54.26=67.83 kN·m

2.考虑竖向荷载与水平地震作用组合

（1）当地震自左向右时，如图5-4-22所示，则

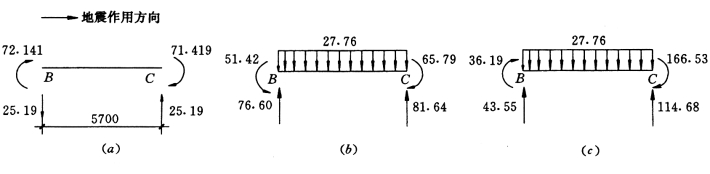
图5-4-22　六层竖向荷载与水平地震作用组合

（a）MEh；（b）MGQ；（c）组合

MBC=γGMGQ+γEhMEh=-1.12×51.42-1.3×72.141=-151.37 kN·m

MCB=γGMGQ+γEhMEh=-1.12×65.79-1.3×72.419=19.16 kN·m

VBC=109.03 kN

VCB=49.20 kN

剪力为零值点距B 点距离为x，则

此截面处跨中弯矩最大，即

考虑到抗震能力调整系数γRE=0.75，则

M=0.75×70.35=52.76 kN·m

（2）当地震自右向左时，如图5-4-23所示，则

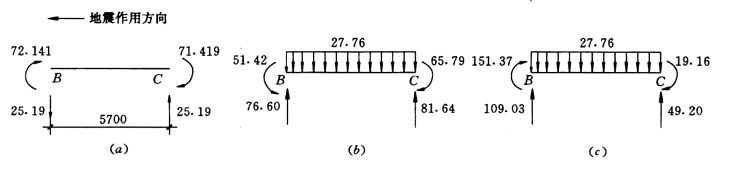
图5-4-23　六层KL—1 竖向荷载与水平地震作用组合

（a）MEh；（b）MGQ；（c）组合

左端弯矩组合值MBC：

MBC=γGMGQ+γEhMEh=-1.12×51.42+1.3×72.141=36.19 kN·m

右端弯矩组合值MCB：

MCB=γGMGQ+γEhMEh=-1.12×51.42-1.3×72.141=-166.53 kN·m

按图5-4-22（c）可求得梁端剪力VBC、VCB

VCB=27.76×5.7-43.55=114.68 kN

剪力为零值点距B 点距离x，则

此截面处跨中弯矩最大，即

考虑到抗震能力调整系数γRE=0.75，则

M=0.75×62.74=47.06 kN·m

⑨轴框架内力组合见表5-4-24。

（三）柱的内力组合

柱的内力组合如下：

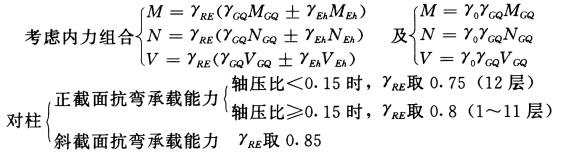
式中，水平地震作用产生的剪力VEh（即各柱的Vim值）已算出，竖向荷载产生的剪力VGQ可根据各柱端弯矩算出。

如12 层边柱：柱顶：

MGQ=37.14kN·m

柱底：

MGQ=31.24kN·m

同理，算出⑨轴12、6、1层各柱剪力。框架柱选取每层柱顶和柱底两个控制截面，从6组内力组合中选取一组配筋最大者作为截面设计控制值。

⑨轴第12、6、1 层柱的组合计算见表5-4-25。

表5-4-25　⑨轴框架柱内力组合表

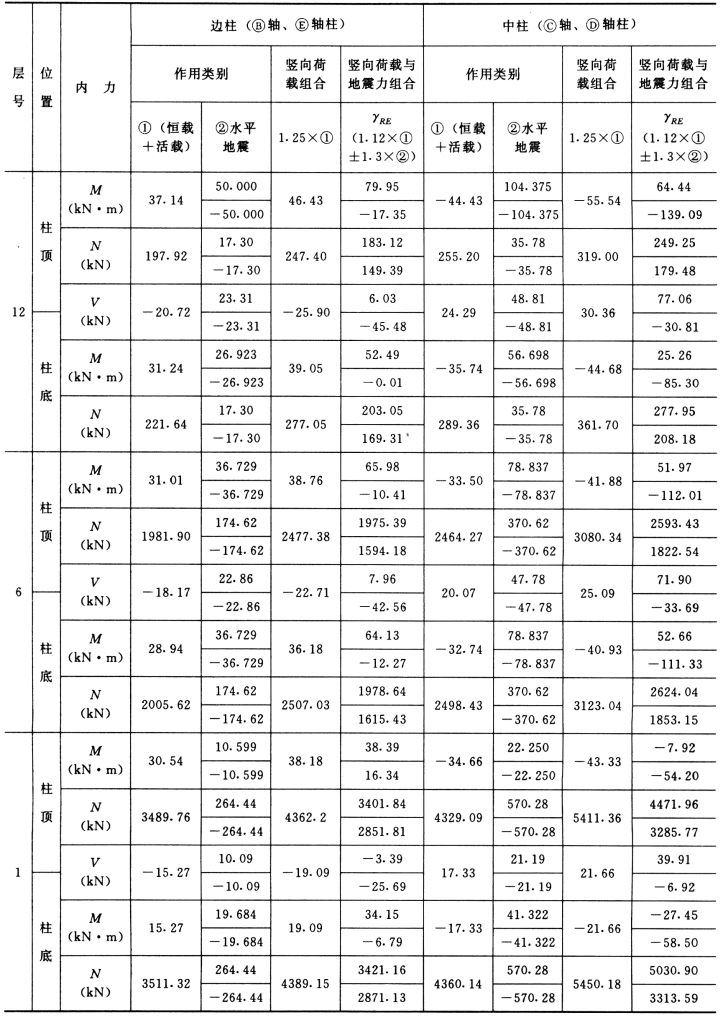
（四）剪力墙内力组合

以⑩轴剪力墙W—1 为例，剪力墙内力组合如下：

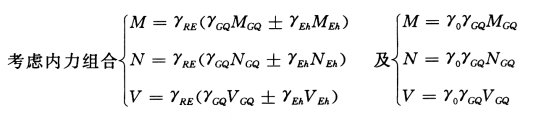
每层剪力墙选取顶端和底端两个控制截面，从6组内力组合中选取一组配筋最大者作为截面设计控制值。

⑩轴第12、6、1 层剪力墙的组合计算见表5-4-26。

表5-4-26　⑩轴剪力墙W—1 内力组合表

（五）连梁内力组合

连梁KL—4 算法同⑨轴框架梁，KL—4 在竖向荷载及水平地震作用下的跨中最大弯矩均在支座处，如表5-4-27所示。

表5-4-27　连梁KL—4 内力组合表

五、截面设计与配筋设计

（一）框架梁（正、斜）截面设计

混凝土强度：6～12 层：（C30），fc=15N/mm2，fcm=16.5N/mm2；

1～5 层：（C40），fc=19.5N/mm2，fcm=21.5N/mm2。

钢筋强度：Ⅰ级钢，fy=210N/mm2；Ⅱ级钢，fy=310N/mm2。

1.正截面受弯承载力计算

（1）边跨（250mm×600m）6 层。

1）跨中截面（M=67.83 kN·m）：

故取下部配筋318（A=763mm2）。

2）支座左截面（M=-113.53kN·m）：

αs=0.086＜αs，max=0.396

ξ=0.090

As=679mm2＞ρminbh0=0.25%×250×565=353mm2

故取上部配筋320（A=941mm2）。

3）支座右截面（M=-124.90kN·m）：

αs=0.095＜αs，max=0.396

ξ=0.100

As=751mm2＞ρminbh0=0.25%×250×565=353mm2

故取上部配筋320（A=941mm2）。

其他层计算略，结果见表5-4-28，边跨实际配筋所有层下部318，上部320。

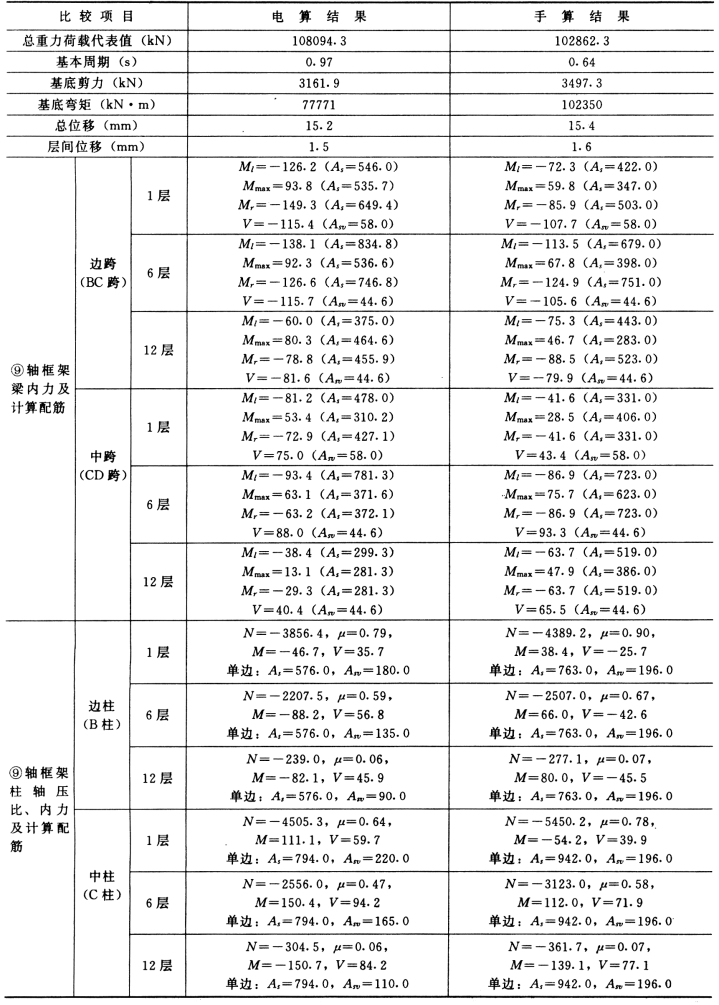
表5-4-28　手算与电算主要结果对比

续表

注 1.内力单位：弯矩，kN·m；剪力、轴力，kN；配筋面积，mm2。
2.框架柱N、M、V分别为内力组合轴力、弯矩、剪力的最大值。
3.剪力墙（Mmax，N）为计算Asw的设计弯矩、设计轴力；（Vmax，N）为计算Aswh的设计剪力、设计轴力。
4.Asw 表示墙柱一端的暗柱配筋面积，Aswh为水平分布筋间距swh范围内水平分布筋面积。

（2）中跨（250×450）6 层

1）跨中截面：M=75.68kN·m，As=623mm2，故取下部配筋318（A=763mm2）。

2）支座截面：M=-86.88kN·m，As=723mm2，故取上部配筋320（A=941mm2）。

其他层计算配筋略，中跨实际配筋所有层下部318，上部320。

2.斜截面抗剪设计（三级抗震）

梁端加密区，剪力设计值由强剪弱弯要求计算

（1）边跨6 层：

Vb=-105.56 kN

剪压比：（满足最小截面尺寸要求）

故

按构造配筋，取双肢箍φ8，s取min（，8d，150），故边跨取2φ8@100。

（2）中跨：

Vb=93.29kN，=0.059，故取2φ8@100

（二）框架柱截面设计

1.柱截面尺寸

验算轴压比：柱净高与截面长边尺寸之比=2.4/0.6=4，为长柱，允许轴压比0.9。柱底及材料改变处（6 层）轴压比见表5-4-28，均满足要求。

2.柱计算长度

无侧移现浇结构：

l0=0.7H

底层：

l0=0.7×3=2.1m

2 层：

l0=0.7×3.9=2.73m

其他层：

l0=0.7×3.3=2.31m

3.柱截面配筋计算

（1）正截面：柱同一截面分别承受正反向弯矩，故采用对称配筋。

边柱：1～5 层：

Nb=fcmbch0ξb=21.5×500×465×0.544=2719.32 kN

6～12 层：

Nb=2086.92 kN

从柱内力组合表可查N 值，对N＞Nb 小偏压，选用M 大N 大的组合；对N≤Nb 大偏压，选用M 大N 小的组合。

1 层边柱均为小偏压，故选M=38.18kN·m、N=4362.2kN 和M=19.09kN·m、Nmax=4389.15kN，取其中配筋较大者。

以M=19.09kN·m、N=4389.15kN 为例。

仅需按构造配筋。

12 层边柱均为大偏压，故选Mmax=79.95kN·m、N=183.12kN 和M=-17.55 kN·m、N=149.39kN，取其中配筋较大者。

以M=79.95kN·m、N=183.12kN 为例。

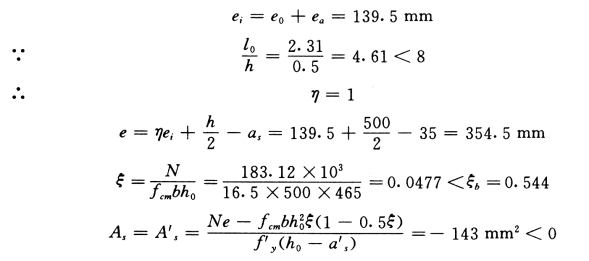
按构造配筋。

边柱：

ρmin=0.7%bchc0=0.007×500×465=1628mm2

实际每侧配筋318（ρ=0.33%＞0.2%），共配818，钢筋截面面积2036mm2（＞1628mm2）。

中柱：1～5 层：

Nb=fcmbch0ξb=21.5×600×565×0.544=23964.94 kN

6～12 层：

Nb=3042.86 kN

1 层中柱：有大偏压柱，也有小偏压柱，故选

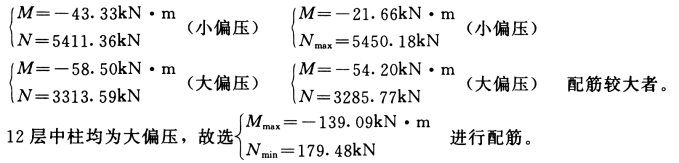
中柱：

ρmin=0.7%bchc0=0.007×600×565=2373mm2

实际每侧配筋320（ρ=0.28%＞0.2%），共配820，钢筋截面面积2513mm2（＞2373mm2），其余计算过程相似，略。

（2）斜截面抗剪（二级抗震）：

为保证强剪弱弯，柱设计剪力值取及内力组合中较大值

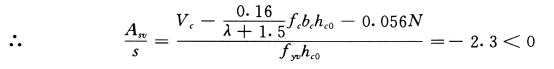
仅需按构造配筋，取复式箍4 肢，4φ10。

按体积配箍要求ρsv=1.2%，

按构造，s 取min（8d，100），所以取复式箍4φ10@100。

长柱柱端加密区长度取max（h0，，500mm），取500mm；非加密区取复式箍4φ10@200。

所有边柱配箍同1 层柱。

同理，中柱柱端加密区配箍取4φ10@100，长度取600mm；非加密区取复式箍4φ10@200。

（三）剪力墙墙肢截面设计

剪力墙抗震等级为二级（一层墙体为加强区），所有层剪力墙均为偏心受压。

1.墙肢截面尺寸及材料

hw=6250mm，bw=250mm，as=a's=300mm，hw0=5950mm

水平及竖向分布筋网片：Ⅰ级钢 fy=210N/mm2

端部明柱加强筋：Ⅱ级钢 fy=310N/mm2

（1）墙肢竖向钢筋计算：

1 层网片为双网φ8@150 双向，构造配筋率0.25%，在hw0范围内共42 排。

大小偏心受压界限的判别：

∵ξ＜ξb，∴为大偏压。

分布钢筋抵抗弯矩：

端部筋为

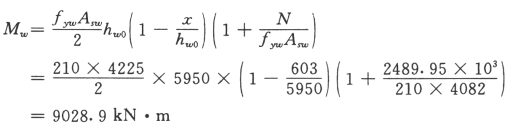
构造配筋：中柱：

As=0.012Ac=4320mm2

边柱：

As=3000mm2

实配1225（As=5890mm2）。

（2）墙肢斜截面抗剪强度计算：

水平钢筋取φ8@150（双排）。

加强区：

Vw=1.1×1316.10=1447·7 kN

截面尺寸校核：

N＜0.2fcbwhw=0.2×19.5×250×6250=6093.75 kN

∴取

N=3923.58kN

∴取λ=2.06

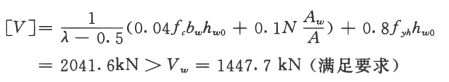
∴竖向分布钢筋与水平钢筋相同，φ8@150（双排）。

其他层计算从略。

实际配筋：端柱1225，竖向分布筋φ8@150，水平分布筋φ8@150。

（四）连梁（正、斜）截面设计

连梁截面尺寸：bb=250mm，hb=400mm，hb0=400-40=360mm，ln=2100-550=1550mm。

1.正截面受弯承载力计算

取6 层

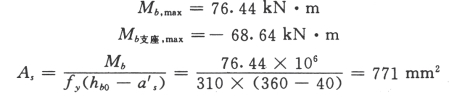
2.斜截面抗剪承载力计算

为了使连梁具有延性，其设计剪力应大于其抗弯极限承载力：

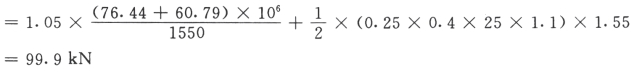
验算截面尺寸：

Vb≤0.2fcbbVb0=0.2×15×250×360=270 kN（满足要求）

需配箍筋：

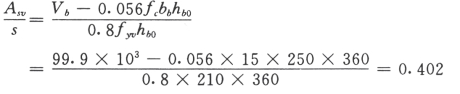
构造要求s取min，实际配箍。

六、手算与电算结果对比分析

采用多、高层建筑结空间有限元分析软件SATWE，对本工程进行了分析设计，手算、电算主要结果见表5-4-28。分析表内数据发现，结构总位移和层间位移手算、电算结果一致，框架梁和连梁手算、电算结果接近，框架柱相差略大，剪力墙差别明显。分析原因，主要有以下几点：

（1）手算近似算法所得周期与计算机计算结果相差较大，导致总的地震作用相差较大。

（2）地震作用下框架—剪力墙协同工作计算，手算采用简化方法，较粗略；计算机计算则采用精确的有限单元法，差别较大。

（3）框架受竖向荷载影响较大，因此手算电算结果接近。

（4）剪力墙受水平荷载影响较大，因而两种方法相差较远。