桥梁正常使用极限状态设计中，预应力的损失具有重要影响，而各项损失又涉及多方面因素，情况较为复杂。因此，各项预应力损失值应首先考虑采用结合工程具体条件由试验确定的数据，对一些大工程尤其需要这样做。当无条件进行试验或无可靠的实测资料时，才取用规范给出的数据和计算方法。一般情况下，主要考虑以下六项预应力损失值，在正常使用极限状态计算中，预应力混凝土构件应考虑由下列因素引起的预应力损失：预应力钢筋与管道壁之间的摩擦σl1；锚具变形、钢筋回缩和接缝压缩σl2；预应力钢筋与台座之间的温差σl3；混凝土的弹性压缩σl4；预应力钢筋的应力松弛σl5；混凝土的收缩和徐变σl6。
其他预应力损失，如预应力钢筋与锚圈口之间摩擦、先张法台座变形引起的损失等，当计算需要时，必须预先通过试验确定，或采用生产厂家及施工单位常年积累的数据。
1.预应力钢筋与管道壁之间摩擦引起的预应力损失
在后张法预应力混凝土结构构件的张拉过程中，由于预留孔道偏差、内壁不光滑及预 应力筋表面粗糙等原因，使预应力筋在张拉时与孔道壁之间产生摩擦。随着计算截面距张 拉端距离的增大，预应力钢筋的实际预拉应力将逐渐减小。各截面实际受拉应力与张拉控制应力之间的这种应力差值，称为摩擦损失。后张法构件张拉时，预应力钢筋与管道壁之间摩擦引起的预应力损失，可按式（10-7）进行计算。
式中 σcon—— 预应力钢筋锚下的张拉控制应力值；
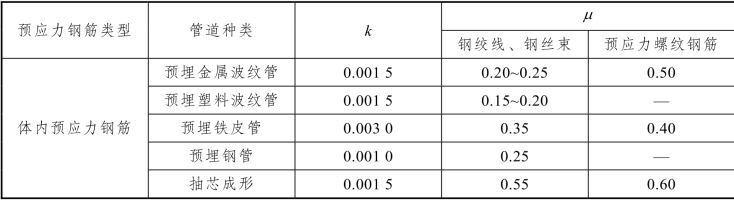
μ —— 预应力钢筋与管道壁的摩擦系数，按表10-1 采用；
θ—— 从张拉端至计算截面曲线管道部分切线的夹角之和（rad）；
k—— 管道每米局部偏差对摩擦的影响系数，按表10-1 采用；
x—— 从张拉端至计算截面的管道长度，可近似地取该段管道在构件纵轴上的投影长度（m）。
表10-1 系数k 和μ 值
由此，可得减小σl1损失的措施：
（1）采用两端张拉，预应力筋经两端张拉后，靠近锚固段一侧预应力筋的应力损失大为减小，损失最大截面转移到构件中部。
（2）在接触材料表面涂水溶性润滑剂，以减小摩擦系数。
（3）提高施工质量，减小钢筋位置偏差。
2.锚具变形、钢筋回缩和接缝压缩引起的预应力损失
预应力钢筋锚固在台座或构件上时，由于锚具、垫板与构件之间的缝隙被挤紧，或者由于钢筋和螺帽在锚具内的滑移，使预应力钢筋回缩，引起预应力损失。
预应力直线钢筋由锚具变形、钢筋回缩和接缝压缩引起的预应力损失，可按式（10-8）进行计算：
式中 Δl —— 张拉端锚具变形、钢筋回缩和接缝压缩值，按表10-2 采用；
l—— 张拉端至锚固端之间的距离；
Ep—— 预应力钢筋的弹性模量。
后张法构件的曲线或折线预应力钢筋，张拉预应力钢筋时，预应力钢筋将沿孔道向张拉端方向移动，此时摩擦力阻止预应力钢筋向张拉端方向移动而产生摩擦损失，但锚固时，预应力钢筋回缩，其移动方向与张拉方向相反，因而将产生反向摩擦。由于反向摩擦的作用，锚具变形引起的预应力损失在张拉端最大，随着与张拉端的距离增大而逐步减小，直至消失。反向摩擦的管道摩擦系数可假定与正向摩擦的相同。
表10-2 锚具变形、钢筋回缩和接缝压缩值
由此可得减小σl2损失的措施：
（1）合理选择锚具和夹具，使锚具变形小或预应力回缩值小。
（2）尽量减小垫块的块数。
（3）增加台座长度。
（4）对直线预应力钢筋可采用一端张拉方法。
（5）采用超张拉，可部分地抵消锚固损失。
3.预应力钢筋与台座之间温差引起的预应力损失
为了缩短先张法构件的生产周期，常在浇捣混凝土后，进行蒸汽养护。升温时，新浇的混凝土尚未结硬，钢筋受热膨胀，但是两端的台座是固定不变的。即台座间距离保持不变，因而张拉后的钢筋就松了。降温时，混凝土已结硬并和钢筋结成整体，显然，钢筋应力不能恢复到原来的张拉值，于是产生了预应力损失。
预应力钢筋与台座之间温差引起的预应力损失σl3可按式（10-9）进行计算。
式中 t2—— 混凝土加热养护时，受拉钢筋的最高温度；t1—— 张拉钢筋时，制造场地的温度。
先张法构件加热养护时，由钢筋与台座温差引起的预应力损失，只是在钢筋与混凝土 尚未黏结的情况下才能发生；当钢筋与混凝土一旦黏结共同工作后，就不再发生因温差引 起的预应力损失。利用这个关系，采用分阶段的养护措施，可以减少钢筋的应力损失：第 一阶段用低温养护，温差控制在20 ℃左右，以此计算预应力损失；待混凝土达到某一强度，其与钢筋的黏结力足以抗衡温差变形，钢筋应力不再损失，再进行第二阶段的高温养护。
4.混凝土弹性压缩引起的预应力损失
当预应力混凝土构件受到预压应力而产生压缩变形时，对于已张拉并锚固于该构件上的预应力钢筋来说，将产生一个与该预应力钢筋重心水平处混凝土同样大小的压缩应变，因而也将产生预应力损失，这就是混凝土弹性压缩损失σl4，它与构件预加应力的方式无关。
对于先张法构件，预应力钢筋张拉与对混凝土施加压应力是先后完全分开的两个工序，当预应力钢筋被放松（放张）对混凝土预加压力时，混凝土所产生的全部弹性压缩应变将引起预应力钢筋的应力损失，可按式（10-10）进行计算：
式中 σpc—— 在计算截面钢筋重心处，由全部钢筋预加力产生的混凝土法向应力；
αEP—— 预应力钢筋弹性模量与混凝土弹性模量的比值。(www.xing528.com)
对于后张法构件，预应力钢筋张拉时混凝土所产生的弹性压缩是在张拉过程中完成的，故对于一次张拉完成的后张法构件，混凝土弹性压缩不会引起应力损失。但是，由于后张法构件预应力钢筋的根数往往较多，一般是采用分批张拉锚固并且多数情况是采用逐束进行张拉锚固的。这样，当张拉后批钢筋时所产生的混凝土弹性压缩变形将使先批已张拉并锚固的预应力钢筋产生应力损失，通常称为分批张拉应力损失，也以 σl4表示。
后张法预应力混凝土构件，当采用分批张拉时，完成张拉的预应力钢筋由后批张拉的预应力钢筋所产生的混凝土弹性压缩引起的预应力损失，可按式（10-11）计算。
式中 Δσpc—— 在计算截面完成张拉的预应力钢筋重心处，由后批张拉预应力钢筋产生的混凝土法向应力。
后张法预应力混凝土构件，当同一截面的预应力钢筋逐束张拉时，由混凝土弹性压缩引起的预应力损失，可按下列简化公式计算：
式中 m—— 预应力钢筋的束数；
Δσpc—— 在计算截面的全部预应力钢筋重心处，由张拉一束预应力钢筋产生的混凝土法向压应力（MPa），取各束的平均值。
后张法构件，往往配置很多纵向预应力钢筋，其中有较多预应力钢筋要弯起，而且它们总是逐束张拉的，按公式（10-11）计算预应力损失，首先要计算每束后批张拉的预应 力钢筋在完成张拉钢筋的重心处产生的混凝土法向预压应力Δσpc，这是一个烦琐的计算过程，除非利用电算程序，手工计算是有一定难度的。为此计算后张法构件由混凝土弹性压缩引起的预应力损失的简便方法采用公式（10-12），该方法是假定每束预应力钢筋的预加力相同，且取它们弹性压缩损失的平均值建立起来的，所以是一个近似的简化方法。
分批张拉的后张法构件，由于每批预应力钢筋的应力损失不同，则实际有效预应力不等，可采用重复张拉先张拉过的预应力钢筋来进行弥补。
5.预应力钢筋松弛引起的预应力损失
钢筋在高应力下，具有随时间而增长的塑性变形性能，钢筋长度保持不变时，表现为随时间而增长的应力降低，称为松弛。钢筋的松弛会引起预应力钢筋中的应力损失，其值因钢筋的种类而异。
预应力钢筋松弛引起的预应力损失，可按式（10-13）计算。
（1）预应力钢丝、钢绞线。
式中 ψ —— 张拉系数，一次张拉时，ψ＝1.0；超张拉时，ψ＝0.9。
ζ —— 钢筋松弛系数，Ⅰ级松弛（普通松弛），ζ＝1.0；Ⅱ级松弛（低松弛），ζ ＝0.3。
σpe—— 传力锚固时的预应力钢筋应力，对后张法构件，σpe＝σcon- σl1-σl2-σl3- σl4；
对先张法构件，σpe＝σcon- σl2。
（2）预应力螺纹钢筋
一次张拉：
超张拉：
6.混凝土收缩、徐变引起的预应力损失σl6
由于混凝土的收缩和徐变变形，预应力混凝土构件将缩短，预应力钢筋也随之缩短，进而引起预应力损失。混凝土收缩、徐变引起的预应力损失，可按下列公式计算：
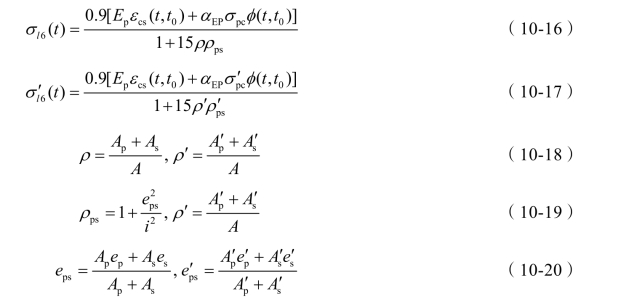
式中 σl6( t )、σl′6( t)—— 构件受拉区、受压区全部纵向钢筋截面重心处由混凝土收缩、徐变引起的预应力损失；
σpc、σp′c—— 构件受拉区、受压区全部纵向钢筋截面重心处由预应力产生的混凝土法向压应力。此时，预应力损失值仅考虑预应力钢筋锚固时（第一批）的损失，普通钢筋应力σl6( t )、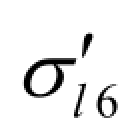
( t)应取为零；σpc、σp′c值不得大于传力锚固时混凝土立方体抗压强度 f′c u的0.5 倍；当σp′c为拉应力时，应取为零。计算σpc、σp′c时，可根据构件制作情况考虑自重的影响；
Ep—— 预应力钢筋的弹性模量；
αEP—— 预应力钢筋弹性模量与混凝土弹性模量的比值；
ρ 、ρ′—— 构件受拉区、受压区全部纵向钢筋配筋率；
A—— 构件截面面积，对先张法构件，A ＝ A0；对后张法构件，A ＝ An；
i—— 截面回转半径，i2＝I /A，先张法构件取I ＝ I0，A ＝ A0；后张法构件取I ＝ In，A ＝ An；
ep、ep′—— 构件受拉区、受压区预应力钢筋截面重心至构件截面重心的距离；
es、es′—— 构件受拉区、受压区纵向普通钢筋截面重心至构件截面重心距；
eps、ep′s—— 构件受拉区、受压区预应力钢筋和普通钢筋截面重心至构件截面重心轴的距离；
εcs( t , t0)—— 预应力钢筋传力锚固龄期为 t0，计算考虑的龄期为t 时的混凝土收缩应变；其终极值 εcs( tu, t0)按表10-3 取用。
( t , t0)—— 加载龄期为 t0，计算考虑的龄期为t 时的徐变系数；其终极值( tu, t0)按表10-4取用。
表10-3 混凝土收缩应变终极值 εcs( tu, t0) ×10-3
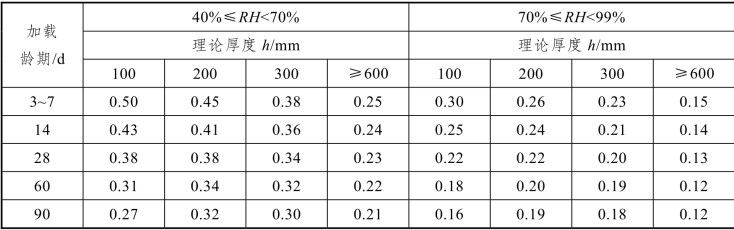
表10-4 混凝土徐变系数终极值( tu, t0)
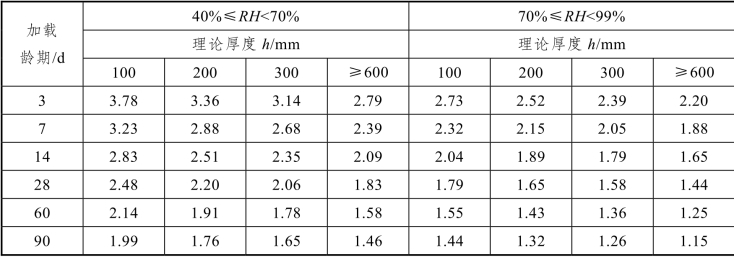
注：① 本表适用于由一般的硅酸盐类水泥或快硬水泥配制而成的混凝土。
② 本表适用于季节性变化的平均温度 -20~ +4 0℃。
③ 表中数值系按强度等级C40 混凝土计算所得，对C50 及以上混凝土，表列数值应乘以
，式中 fck为混凝土轴心抗压强度标准值（MPa）。
④ 计算时，表中年平均相对湿度40≤RH<70%，取RH＝55%；70≤RH <99%，取RH ＝80%。
⑤ 表中理论厚度h＝2 A /u，A 为构件截面面积，u 为构件与大气接触的周边长度。当构件为变截面时，A 和u 均可取其平均值。
⑥ 表中数值按10 年的延续期计算。
⑦ 构件的实际传力锚固龄期、加载龄期或理论厚度为表列数值中间值时，收缩应变终极值可按直线内插法取值。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
