如何设计单筋矩形截面梁：计算截面承载力

1.计算公式

根据受弯构件正截面承载力计算的基本原则，可以得到单筋矩形截面受弯构件承载力计算简图5-2。

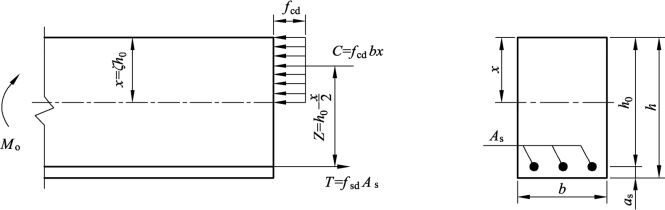
图5-2　单筋矩形截面受弯构件正截面承载力计算图式

由截面上水平方向内力之和为零的平衡条件，即T + C＝ 0，可得到

由截面上对受拉钢筋合力T 作用点的力矩之和等于零的平衡条件，可得到

由对压区混凝土合力C 作用点取力矩之和为零的平衡条件，可得到

式中 Mu—— 计算截面的抗弯承载力；

fcd—— 混凝土轴心抗压强度设计值；

fsd—— 纵向受拉钢筋抗拉强度设计值；

As—— 纵向受拉钢筋的截面面积；

x—— 按等效矩形应力图计算的受压区高度；

b—— 截面宽度；

h0—— 截面有效高度。

式（5-1）、式（5-2）和式（5-3）仅适用于适筋梁，而不适用于超筋梁和少筋梁。因为超筋梁破坏时钢筋的实际拉应力并未到达抗拉强度设计值，故不能按 fsd来考虑。因此，公式的适用条件为：

（1）为防止出现超筋梁情况，计算受压区高度x 应满足

由式（5-1）可得

相对受压区高度为

当ζ ＝ ζb时，可得适筋梁的最大配筋率为(www.xing528.com)

显然，适筋梁的配筋率μ 应满足

式（5-4）和式（5-8）具有相同的意义，目的都是防止造成超筋梁。

（2）为防止出现少筋梁情况，配筋率应满足

受弯构件的正截面计算，一般仅需对构件的控制截面进行。所谓控制截面，在等截面受弯构件中，是指弯矩组合设计值最大的截面；在变截面受弯构件中，除了弯矩组合设计值最大的截面外，还有截面尺寸相对较小，而弯矩组合设计值相对较大的截面。受弯构件正截面承载力计算，在实际设计中可分为截面设计和截面复核两类计算问题。

2.截面设计

截面设计是指根据截面上的弯矩组合设计值，选定材料、确定截面尺寸和配筋的计算。在桥梁工程中，最常见的截面设计工作是已知受弯构件控制截面上作用的弯矩计算值（M＝γ0Md）、材料强度级别和截面尺寸，对截面进行配筋。截面设计方法及计算步骤如下：

已知弯矩计算值M，混凝土和钢筋材料级别，截面尺寸b × h，求钢筋面积 As。

（1）假设钢筋截面重心到截面受拉边缘距离 as。在Ⅰ类环境条件下，对于绑扎钢筋骨架的梁，可设 as≈40 mm （布置一层钢筋时）或65 mm（布置两层钢筋时）。对于板，一般可根据板厚假设 as为30 mm 或40 mm，这样可得到有效高度 h0。

（2）由式（5-2）求得受压区高度x，并满足x≤ζbh0。

（3）由式（5-1）求得钢筋面积 As。

（4）根据选择钢筋直径并进行截面布置后，得到实际配筋面积 As、as及 h0。实际配筋率μ应满足μ ≥μmin。

3.截面复核

截面复核是已知截面尺寸、混凝土强度级别和钢筋在截面上的布置，要求计算截面的承载力Mu或复核控制截面承受某个弯矩计算值是否安全。截面复核方法及计算步骤如下：

已知截面尺寸b、h，混凝土和钢筋材料级别，钢筋面积 As及 as，求截面承载力Mu。

（1）检查钢筋布置是否符合规范要求。

（2）计算配筋率μ ，且应满足μ ≥μmin。

（3）由式（5-5）计算受压区高度x。

（4）然后由式（5-8）、式（5-9）计算截面承载力Mu。

若计算受压区高度x>ζbh0，则为超筋截面，此时，令x＝ζbh0，计算Mu。

（5）若 γ0Md≤Mu，则承载力满足设计要求。