数学模型：描述曲线的方法

曲线主要包括基本曲线、二次曲线和自由曲线。其中，基本曲线包括直线、圆弧和圆等。二次曲线包括椭圆、双曲线、抛物线、螺旋线和一般二次曲线等。自由曲线又分为Bézier（贝塞尔）曲线、B样条曲线和非均匀有理B样条曲线等。自由曲线是一般函数不能表达的曲线。现实生活中这种曲线比比皆是，如汽车发动机的气道等。基本曲线和二次曲线比较简单，不再叙述，下面主要对自由曲线进行简要的介绍。

1.Bézier（贝塞尔）曲线

Bé zier曲线的每一段k阶曲线可以表示如下：

式中：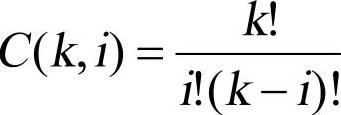

Bé zier曲线是曲线造型中的一个里程碑，它以逼近原理为基础，应用Bé zier曲线逼近自由曲线或由设计师勾画的草图，真正起到“辅助设计”的作用。Bé zier曲线在CAD/CAM领域发挥了重要的作用。

Bé zier曲线也有其缺点。首先，Bé zier曲线不具备局部性，即特征多边形的每一个控制点都对曲线的形状产生影响，修改一处就会影响整条曲线的形状，故不能作局部修改；其次，当曲线的形状复杂时，需要增加特征多边形的顶点数，曲线的幂次也随之增高，从而增加了计算量；最后，当曲线的幂次较高时，Bézier曲线的形状与其定义的多边形有较大差异时，不够直观。吸收Bézier曲线的优点，去除其缺点，就产生了B样条曲线。(www.xing528.com)

2.B样条曲线

B样条曲线的参数方程表示如下：

式中Q_i是控制点；N_k,j(u)为基函数；k为B样条曲线的阶次。B样条曲线的基函数可以递推。

式中u_i为节点值。若节点值等间隔，则对应均匀B样条曲线，否则为非均匀B样条曲线。三阶B样条曲线的形式为：

均匀B样条曲线的特点是节点等距分布，由于各节点集形成B样条函数相同，故可看作同一条B样条曲线的简单平移。一般情况下，应用均匀B样条方法可获得满意的结果，而且计算效率高。但均匀B样条曲线存在如下问题：1）不能贴切地反映控制顶点的分布特点；2）当型值点分布不均匀时，难以获得理想的插值曲线。对于这两种情况，可借助非均匀B样条曲线以获得良好的效果。此外，在自由曲线设计中经常会遇到传统的圆锥曲线，但无论是均匀B样条曲线还是非均匀B样条曲线都不能对其作精确表示。在此种情况下，需要应用均匀有理B样条曲线，即NURBS曲线。NURBS曲线可以用同一的方式表示一条由直线、圆锥曲线和自由曲线构造的复合曲线。