曲线与曲面的结构特征分析

在工程设计时，造型曲线是创建曲面的基础，曲线创建得越平滑，曲率越均匀，则获得曲面的效果将越好。此外使用不同类型的曲线作为参照，可创建各种样式的曲面效果，例如使用规则曲线创建规则曲面，而使用不规则曲线将获得不同的自由曲面效果。

曲线的结构特征

曲线可看作是一个点在空间连续运动的轨迹。按点的运动轨迹是否在同一平面，曲线可分为平面曲线和空间曲线；按点的运动有无一定规律，曲线又可分为规则曲线和不规则曲线。

因为曲线是点的集合，所以画出曲线上的一系列点的投影，并将各点的同面投影依次光滑连接，就得到该曲线的投影，这是绘制曲线投影的一般方法。若能画出曲线上一些特殊的点，如最高点、最低点、最左点、最右点、最前点及最后点等，则可更确切地表示曲线。

曲线的投影性质

曲线的投影一般仍为曲线，如图1-9所示曲线L，当它向投影面进行投影时，形成一个投射柱面，该柱面与投影平面的交线必为一曲线，故曲线的投影仍为曲线。属于曲线的点，它的投影属于该曲线在同一投影面上的投影。如图1-9所示点D属于曲线L，则它的投影点d必属于曲线的投影I；属于曲线某点的切线，它的投影与该曲线在同一投影面的投影仍相切于切点的投影。

曲线的阶次

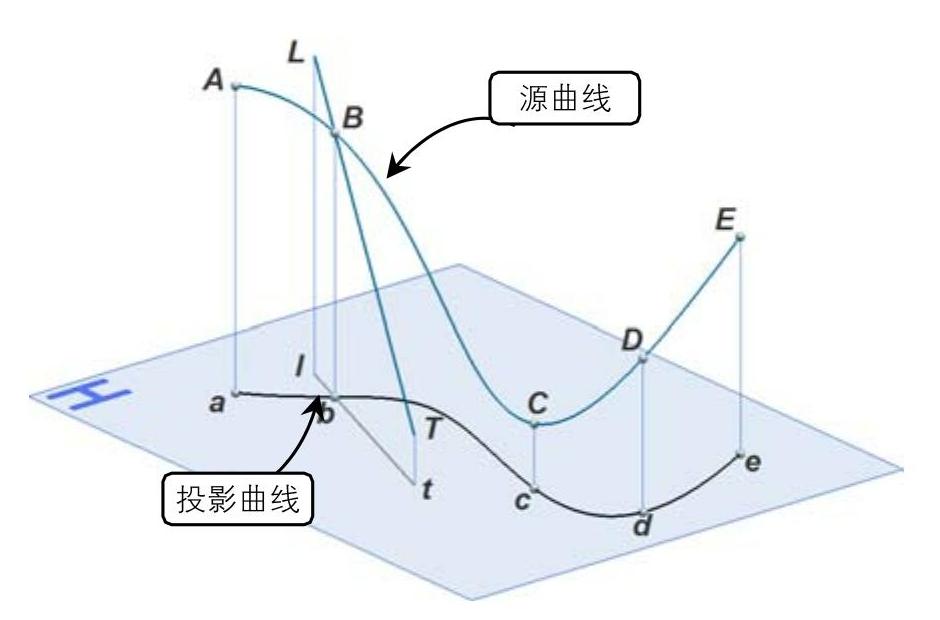
图1-9 曲线投影到指定平面上

由不同幂指数变量组成的表达式称为多项式。多项式中最大指数称为多项式的阶次，例如：6X³+3X³－8X=10(阶次为3阶)，5X⁴+6X³－7X=10（阶次为4阶）。

曲线的阶次用于判断曲线的复杂程度，而不是精确程度。简单一点说，曲线的阶次越高，曲线就越复杂，计算量就越大。而使用低阶曲线更加灵活，更加靠近它们的极点，使得后续操作（显示、加工、分析等）运行速度更快，也便于与其他CAD系统进行数据交换，因为许多CAD只接受3次曲线。

使用高阶曲线常常会带来如下弊端：灵活性差，可能引起不可预知的曲率波动，造成与其他CAD系统数据交换时的信息掉失，使得后续操作（显示、加工、分析等）运行速度变慢。一般来讲，最好使用低阶多项式，这就是为什么在UG等CAD软件中默认的阶次都为低阶的原因。

规则曲线

规则曲线就是按照一定规律分布的曲线。规则曲线根据结构分布特点可分为平面和空间规则曲线，分别介绍如下：

平面规则曲线：凡曲线上所有的点都属于同一平面，则该曲线称为平面曲线。常见的圆、椭圆、抛物线和双曲线等可以用二次方程描述。平面曲线除具有上节所述的投影性质外，还有下列投影性质：平面曲线所在的平面平行于某一投影面时，则在该投影面的投影，反映曲线的实形，如图1-10所示；平面曲线所在的平面垂直于某一投影面时，则在该投影面的投影，积聚成一条直线；平面曲线上某些奇异点的投影保持原有性质，即曲线的拐点、尖点及两重点投影后仍为曲线投影的拐点、尖点及两重点。此外，抛物线、双曲线、椭圆的投影为椭圆。

空间规则曲线：凡是曲线上有任意四个连续的点不属于同一平面，则称该曲线为空间曲线。常见的空间规则曲线有圆柱螺旋线和球面螺旋线，如图1-11所示。

不规则曲线又称自由曲线，是指形状比较复杂、不能用二次方程准确描述的曲线。自由曲线广泛用于汽车、飞机、轮船的计算机辅助设计中。其涉及的问题有两个方面：一是对已知自由曲线，通过交互方式加以修改，使其满足设计者的要求；二是由已知的离散点确定曲线。使用平面离散点获得曲线特征必须首先通过拟合方式形成光滑的曲线。离散点确定了曲线的大致形状，拟合就是强制曲线沿着这些点绘制出样条曲线，通常情况下,为创建更加光滑的曲线，可将几个曲线段彼此首尾相连拼接，这就要求曲线连接处有连续的一阶和二阶导数，从而保证各曲线段的光滑连接。拟合曲线可以通过下面两种方法获得。

图1-10 创建平面规则曲线

(www.xing528.com)

图1-11 圆柱和球面螺旋曲线

插值拟合：该方法要求构造的曲线依次通过一组离散点（称为型值点）并满足光滑性要求，称作插值样条曲线。在设计的最初阶段，型值点的确定往往是不精确地，需要修改，而插值曲线不能直接通过修改离散点的坐标控制和修改曲线的形状，如图1-12所示。以插值方法构造的自由曲线，一般用于绘图或动画设计。

逼近拟合：要求构造的曲线最逼近所给定的数值点（称为控制点），称作逼近样条曲线。将控制点用直线段连接起来，称为曲线的控制图（或称为控制多边形），如图1-13所示。包含一组控制点的凸多边形边界称为“凸包”，每个控制点均在凸包之内或凸包边界上，曲线以凸包为界，保证沿控制点平滑前进。凸包提供了曲线与控制点区域间的偏差测量。

曲面的结构特征

在工程上经常会遇到各种曲面，如某些机器零件的表面、飞机机身、汽车外壳以及船体表面等，为了表示这些曲面，必须熟悉曲面的形成和创建方法。由于曲线分为规则与不规则曲线，则使用这些曲线参照所获得的曲面同样有规则和不规则曲面两类，分别介绍如下：

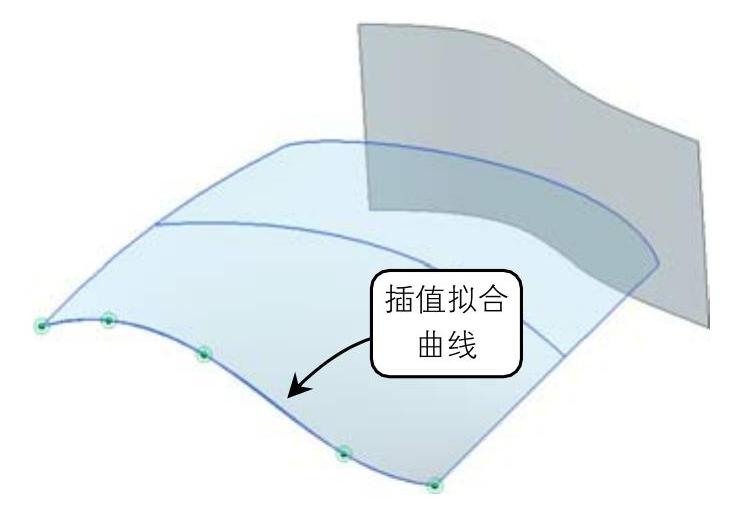
图1-12 插值拟合曲线

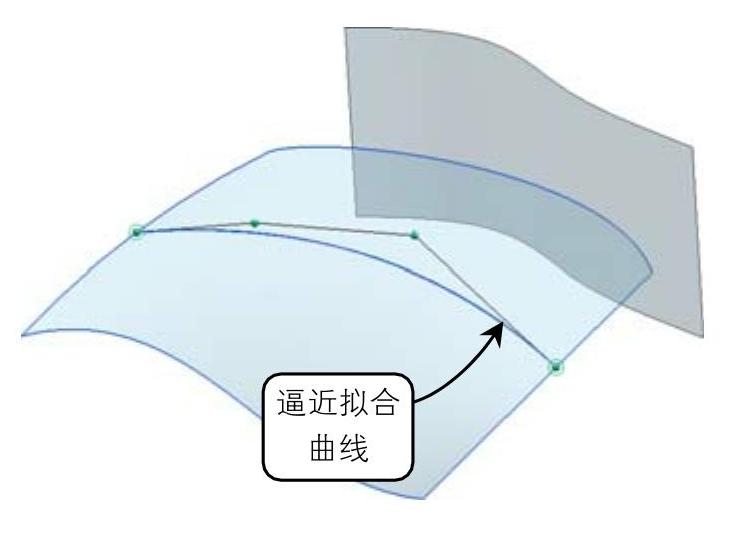
图1-13 逼近拟合曲线

规则曲面

规则曲面可看作是一条母线按照一定规律运动所形成的轨迹，母线在曲面上的任何一个位置统称为曲面的素线，而控制母线做规则运动的一些不动的几何元素称为导元素。按母线的形状不同，常见的规则曲面可分为直纹和曲纹曲面。其中，直母线形成的曲面称为直纹曲面，它又可分为单曲面和扭曲面；由曲母线形成的曲面称为曲纹曲面，它又可分为定线曲面和变线曲面。

既然规则曲面由母线沿导元素运动而成，故表示一个曲面时，必须首先表示该曲面的母线及导元素，这样该曲面的性质就被确定。然后为了清晰起见，还需画出该曲面上的轮廓线及外视转向线。对于复杂的曲面，还需表示出曲面上的某些素线或交线。例如利用柱状面创建螺旋输送器曲面特征，正螺旋柱状面的两条曲导线皆为圆柱螺旋线，连续运动的直母线始终垂直于圆柱轴线，效果如图1-14所示。

不规则曲面

随着汽车和飞机制造工业的发展，对自由曲面建模提出了更高的要求，现代研究方法突破了许多运动学理论和工程实践问题。有效解决了不规则曲面的设计难题，使用不同的方法可创建不同的自由曲面。一条自由曲线可以由一系列的曲线段连接而成。类似地，一个自由曲面也可以看作是由一系列曲面拼合而成，如图1-15所示。

图1-14 圆柱螺旋曲面

图1-15 自由曲面工具获得的电熨斗曲面