相图计算原理及其基础吉布斯相律

CALPHAD是calculation of phase diagrams的简称，译作相图计算。该方法于1908年由Van Laar提出，并将吉布斯自由能正规溶液模型引入，但由于缺乏一些必要的数据，其未能将数学表达式转化为真实合金体系的相图。20世纪70年代以来，随着热力学、统计力学和溶液理论、计算机技术的进步，Kaufman、Hillert和Ansara等人逐渐将相图研究从以相平衡的实验测定为主，发展为热化学与相图的计算机耦合研究为主的新阶段，乃至最终成长为介于热化学、相平衡和溶液理论、计算机技术之间的交叉学科分支——CALPHAD［51，52］。

以往相图的测定主要是依靠实验方法，但即便精确测定一个二元相图，其工作量也是相当巨大的［52］，而科研与工业生产中更多的是需要三元及以上多元体系构成的材料，因此相图测定的实验方法已不能满足实际需求［53］。利用CALPHAD方法计算相图，可以使人们利用较为成熟的热力学知识和已有的资料及实验数据，绕过某些实验困难（如高温高压及强腐蚀性体系面临的苛刻条件和容器选择）预测体系的相图，或者由易测准的部分来预测实验中难测准的部分，提高准确性［54-56］。另外，在二元和三元系等低组元体系热力学参数的基础上，通过外推或添加少量的多元参数可获取多元体系的相图和热力学信息［57，58］。

由CALPHAD方法来获得计算相图，由于热力学与相图之间的高度自洽性等优点，使该方法成为溶液理论及相图研究中最为活跃的领域之一［52］。同时，多元多相平衡计算方法的成熟，数据库和计算软件的完善，以及具有实用价值的多元体系计算相图的构筑和CALPHAD方法在物理性质预测中的一系列应用，使得CALPHAD方法逐渐成为材料设计和模拟的重要工具［52］。

研究者可以充分利用相图计算的方法，将计算与一些关键性的实验结合起来，达到低成本、省时的制备不同液态金属合金材料的目的。相图计算常用软件有PANDAT［59］、FactSage［60，61］、MTDATA［62］、Thermo-Calc［63］等。在使用相图计算方法时，有时需要进行必要的实验验证，常用的实验方法可以分为动态和静态两种，前者包括淬火法［64］、扩散偶法［65］、X射线结构分析［66］等，后者有热分析法［67］、电阻法、热膨胀法［68］等。

3.4.1.1　相图计算原理

相图计算方法是基于吉布斯自由能随温度、压力、组分的变化而变化这一热力学原理。在恒温恒压下就是研究吉布斯自由能与组成的关系，即吉布斯自由能-组成图。由吉布斯自由能最低原理可知，任何一个体系，在一定的组成范围内，吉布斯自由能最低的相就是最稳定的相，自由能高的相就是不稳定的相。在不同的组成范围内，根据相区接触规则，两稳定相区之间必为两相共存区，从而由不同组成范围的吉布斯自由能-组成图可以得到相图［69］。如果已知低组元（二、三组元）系统的热力学模型参数，就可以通过外推得知多组元系统中每个相的吉布斯自由能函数，进而就可以计算出多组元系统的相图。

在使用相图计算方法时，需要用到大量的热力学数据，因此有必要建立一个热力学数据库。这个数据库应包含相应系统的模型信息，以及各种参数的表达式和数值，例如各个纯组元在参考状态下的吉布斯自由能表达式，每种中间相化合物的吉布斯自由能，每种相的体积分数、活度和形成焓等。而那些不能从数据库获取的模型参数则可以通过实验和优化的方式得到。在所有相的热力学模型和参数确定之后，体系的相图就可以通过软件计算出来［51］，图3.5显示了相图计算的原理框架。

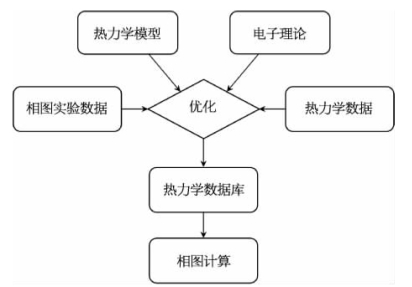
图3.5　相图计算的原理［70］

相律是相图计算的理论基础，由吉布斯于1875年总结导出，故常称为吉布斯相律。吉布斯相律表达了热平衡体系中所含的相数、组分数、自由度数及影响体系平衡状态的外界因素之间的关系，其数学表达式为

其中，f为自由度，C为组元数，P为相数，2是指温度和压力两个外界因素。相律给出了所有体系处于平衡状态时所要满足的条件，对平衡体系的研究具有指导作用。

对单组元体系，C=1，自由度的数目为f=3-P。单组元体系两相平衡时，f=1，说明P和T两个强度量中只有一个是可以任意改变的，另一个是因变量，它们之间存在着一定的函数关系，用热力学理论获得这个函数关系，即为克拉珀龙（Clapeyron）方程：

式中，T为相变温度，ΔVm为两相摩尔体积差，ΔHm为摩尔相变潜热。应用克拉珀龙方程，可以求出单组元体系相图中的两相平衡线P=f（T）。

对一个多元体系，总的摩尔自由能为

其中，φ为体系中相的个数，Pv为v相的摩尔分数，Gv为v相的摩尔自由能，Gv可以表达为

这里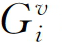，和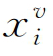分别为具有v相结构的纯组元i的摩尔自由能和摩尔分数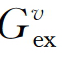，为过剩自由能。固相和液相之间达到平衡的条件为(www.xing528.com)

1）组元i在每个相中的化学势均相等，即

或者

2）总的自由能达到最小值，即

此外，

如果已知的解析表达式，则该体系的相图就可以计算出来。

3.4.1.2　热力学模型

设纯组元的吉布斯自由能为，它可以表达为［71］

这里，最后两项a6·T7和a7·T-9分别是对低于熔点和高于熔点的相的修正项，为组元i在参考态（298.15 K和1 bar）下的焓，a0，a1，a2，a3…为待定参数，通过对纯组元的热容、相变温度和相变时的焓变等数据进行拟合得到，的值通常是在Dinsdale编辑的SGTE（Scientific Group Thermodata Europe）数据库中查询得到。

对二元系来说，采用替代溶液模型，则φ相的吉布斯自由能可以表示为

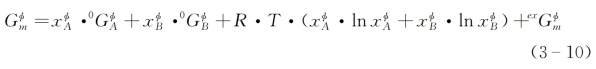
其中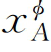，和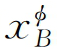分别为φ相中组元A和B的摩尔分数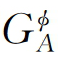，0和0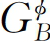分别为纯组元A和B的吉布斯自由能，R为普适常数，ex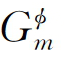为φ相中的过剩吉布斯自由能，可以表示为

上式称为Redlich-Kister（RK）多项式，其中j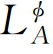，B为j阶二元交互作用参数，通常是温度T的线性函数，可以表达为［72］

其中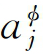，j和j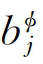是待定参数。