低压系统短路电流计算及优化措施

一、概述

1.短路的类型

短路故障分为对称短路和不对称短路。三相短路是对称性短路，造成的危害最为严重，但发生三相短路的机会较少。其他种类的短路都属于不对称短路，其中单相短路发生的机会最多，约占短路总数中的70%以上。图7-1画出了短路的各种类型和相应的代表符号。

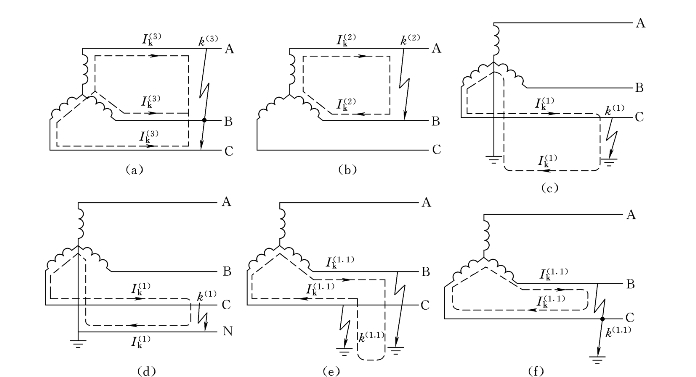
图7-1 短路的各种类型

（a）三相短路；（b）两相短路；（c）单相接地短路；（d）单相短路；（e）两相接地短路；（f）两相短路接地

2.短路电流计算的目的

为了保证电力系统安全运行，在设计选择电气设备时，都要用可能流经该设备的最大短路电流进行热稳定校验和动稳定校验，以保证该设备在运行中能够经受住突发短路引起的发热和电动力的巨大冲击。同时，为了尽快切断电源对短路点的供电，继电保护装置将自动地使有关断路器跳闸。继电保护装置的整定和断路器的选择，也需要准确的短路电流数据。

3.短路计算的假定条件

短路过程是一种暂态过程。影响电力系统暂态过程的因素很多，若在实际计算中把所有因素都考虑进来，将是十分复杂也是不必要的。因此，在满足工程要求的前提下，为了简化计算，通常采取一些合理的假设，采用近似的方法对短路电流进行计算。

基本假设条件如下：

（1）在短路过程中，所有发电机电势的相位及大小均相同，亦即在发电机之间没有电流交换，发电机供出的电流全部是流向短路点的。而所有负荷支路则认为都已断开。

（2）不计磁路饱和。这样，系统中各元件的感抗便都是恒定的、线性的，可以运用叠加原理。

（3）不计变压器励磁电流。

（4）系统中所有元件只计入电抗。但在计算短路电流非周期分量衰减时间常数，或者计算电压为1kV以下低压系统短路电流时，则须计及元件的电阻。

（5）短路皆为金属性短路，即不计短路点过渡电阻的影响。

（6）三相系统是对称的。对于不对称短路，可应用对称分量法，将每序对称网络简化成单相电路进行计算。

以上假设，使短路电流计算结果稍偏大一些，但最大误差一般不超过10%～15%，这对于工程设计所要求的准确度来说是允许的。

4.典型的短路电流波形曲线

为校验各种电气设备，必须找出可能出现的最严重的短路电流。经分析，发现在空载线路上且恰好当某一相电压过零时刻发生三相短路，在该相中就会出现最为严重的短路电流。因此，常常把这种情况下的短路电流波形曲线，作为典型的短路电流波形曲线，见图7-2。

图7-2中，短路电流瞬时值ik是由周期分量ip和非周期分量inp合成的，即：

式中

ip——短路电流的周期分量，Ipm为其幅值，ip=-Ipmcosωt；

inp——短路电流的非周期分量，按指数规律衰减，；

Ta——短路电流非周期分量衰减时间常数，；

L∑、X∑、R∑——短路点到电源的总电感、总电抗和总电阻。

从图7-2中还可以看出，当短路初瞬（t=0s），周期分量为负的最大值，而非周期分量则为正的最大值，使合成短路电流从零开始，迅速增大，在t=0.01s时出现一个最大的短路全电流瞬时值，被称为三相短路冲击电流ish，其值可从下式求出：

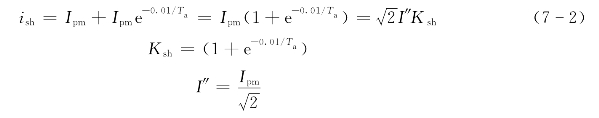
式中 I″——短路电流周期分量在第一个周期内的有效值，被称为次暂态短路电流；

Ksh——短路电流的冲击系数，1＜Ksh＜2，其值与短路回路的时间常数Ta有关。

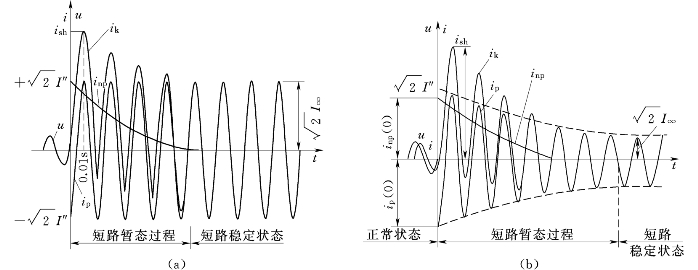
图7-2 典型的短路电流波形曲线

（a）无限大系统供电；（b）有限容量系统供电

短路全电流最大有效值用Ish表示，可由下式计算：

短路电流非周期分量inp约经10个周波左右即衰减为零，此后短路电流中只剩下周期分量，称为稳态短路电流，其有效值用I∞表示（读成I无穷大）。

图7-2（a）所示为由无穷大电源供电的系统，短路电流周期分量的幅值是恒定不变的，因而有：

I″=I∞=It

式中 It——任意时刻周期分量的有效值。

图7-2（b）所示为有限大容量电源供电的系统，短路电流周期分量的幅值也是随时间而变化的。此时I″可能大于I∞，但也可能小于I∞。

二、采用标幺值的电力网等值电路

标幺值是一种无量纲的相对值。在短路计算中，采用标幺值比采用有名值更为方便。

1.标幺值的定义和基准值的确定

在短路计算中，一般取容量基准值为100MVA（也可以取为1000MVA或其他值），各级电压的基准值就取为各级平均电压，表示为：

Sd=100MVA

Ud=Uav

电流基准值和阻抗基准值则需由上述两基准值算出：

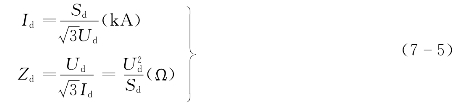
2.化标幺的第一种方法：统一化标幺

将原始网络先用折算的方法画出有名值等值电路，再将各元件有名值除以统一的基准值，即可得出各元件的标幺值。详见例7-1。

【例7-1】 利用例6-1的最后结果，将其有名值等值电路进一步化为标幺值等值电路。因导纳数值很小，略去。与电抗相比，电阻也较小，在短路计算时一般亦可略去不计（电抗前符号j都可略去）。

解：例6-1最后结果略去导纳和电阻后，简化电路图见图7-3。

图7-3 例6-1简化的等值电路（仅计电抗时）

因折算后各元件已处于同一个电压级10.5kV，故各元件电抗值可直接相加：

X∑=0.44+0.37+0.33+0.58+1.21=2.93（Ω）

现用标幺值进行计算。取基准容量为100MVA：

电源电势的标幺值为：

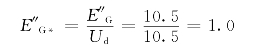
各元件电抗的标幺值为：

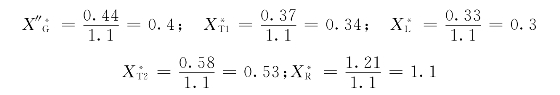
标幺值等值电路见图7-4。各元件电抗标幺值可直接相加：

图7-4 标幺值等值电路

X∑*=（0.4+0.34+0.3+0.53+1.1）=2.67

现将其还原成有名值：

可见与前面的结果完全是一致的。

3.化标幺的第二种方法：就地化标幺

这种方法不必先用折算方法化为有名值等值电路，而是直接用各元件有名值阻抗除以本电压级的阻抗基准值，即可直接计算出各元件的阻抗标幺值：

式中 Z——各元件按本身额定电压（或其平均电压）计算出的有名值阻抗，Ω；

Sd——化标幺时统一规定的容量基准值，MVA；

Ud——本级基准电压（一般采用本级平均电压），kV；

Zd——本电压级的阻抗基准值，Ω。

就地化标幺值方法详见例7-2。

三、三相短路的计算方法

（一）无穷大电源系统供给的短路电流

1.无穷大电源的概念

无穷大电源理论上是指系统容量S→∞，系统电抗Xs→0，其出口分界母线的电压在短路时能够保持不变。实际上，当系统容量很大，加之发电机自动电压调节器及强行励磁装置的作用，以及枢纽变电所无功/电压自动控制装置的作用，在短路时系统某一枢纽变电所高压母线电压是可以保持不变的，这样的大容量系统就可以认为是无穷大电源系统。

2.无穷大电源系统供出的三相短路电流计算方法

无穷大电源系统供出的短路电流周期分量幅值是不衰减的，可以很方便地算得。

（1）直接用有名值计算（根据折算到短路点处的等值电路）：

式中 I″——短路点处的次暂态短路电流（有效值），kA；

Sk——短路点处的短路容量，MVA；

Uav、UN——短路点处的平均电压、额定电压（线电压），kV；

X∑——系统电源到短路点之间的总电抗，Ω；

ish——短路点处的冲击短路电流（瞬时值），kA；

Ksh——短路电流冲击系数。

如果短路点处在低压电网中，电阻R也要计入，则公式中X∑要用Z∑代替，即：

（2）用标幺值进行计算：无穷大系统电源电压保持不变，电源相电压的标幺值即为1.0，故：

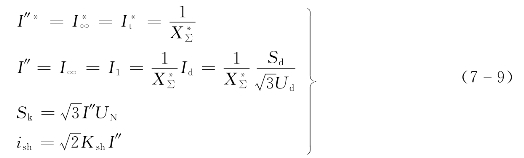
式中 Sd——计算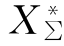时所选用的基准容量，一般选100MVA；

Ud——短路点处的基准电压，一般为该点的平均电压Uav（线电压），kV；

Id——短路点处的基准电流，kA。

（二）有限容量电源供给的短路电流

有限容量电源系统在短路过程中，电源电压是变化的，因而短路电流周期分量的幅值也是随时间变化的。这样，I″≠I∞≠It，不像无穷大系统那样简单了。

在工程实用计算中，一般采用运算曲线法来求取任意时刻的短路电流周期分量有效值It（常需要计算0s时刻的I″；0.1s或0.2s时刻的I0.1、I0.2；4s时刻的I4即稳态短路电流I∞），还要求出短路冲击电流ish。

下面用算例来说明具体计算方法。

【例7-2】 如图7-5所示之电力系统，各元件参数均已标注在图中，求K点发生三相短路时，短路点的短路电流I″、I0.2、I∞和ish。

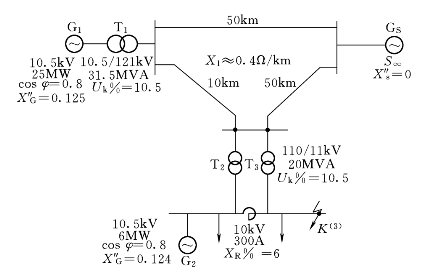
图7-5 电力系统短路原始网络图

解：（1）网络化简步骤。

1）画等值电路图7-6，各电抗按顺序编号。

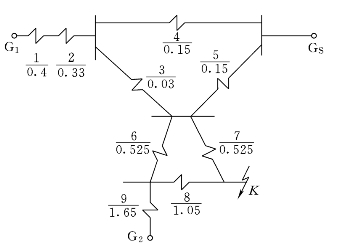
图7-6 等值电路图

2）将3、4、5号电抗组成的三角形网络化成由10、11、12号电抗构成的星形网络，将6、7、8号电抗组成的三角形网络化成由13、14、15号电抗构成的星形网络，如图7-7所示。

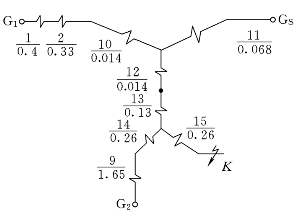
图7-7 等值电路的化简（一）

3）将1、2、10号电抗合并为16号电抗，将12、13号电抗合并为17号电抗；将9、14号电抗合并为18号电抗，如图7-8所示。

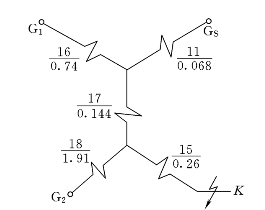
图7-8 等值电路的化简（二）

4）将16、17、11号电抗构成的星形化为由19、20、21号电抗构成的三角形。因21号电抗是连接两个电源的支路，与短路点电流无关，故可略去不画，见图7-9。

5）用星→网变换公式求“转移电抗”。将图7-9的星形化为如图7-10的网形，其中两个电源之间的连接支路均可略去不画。这样，只画出G2到短路点的直连电抗22、G1到短路点的直连电抗23和GS到短路点的直连电抗24。这3个直连电抗22、23、24就分别是电源G2、G1和系统GS对短路点的“转移电抗”。

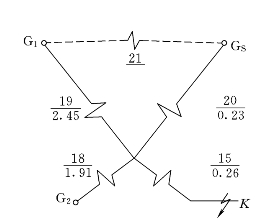
图7-9 等值电路的化简（三）

图7-10 等值电路的化简（四）

（2）参数计算（均用标幺值，为方便省去*号）。

1）各元件参数。取Sd=100MVA，Ud=Uav（本例中分别为115kV和10.5kV）。

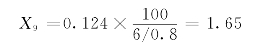
2）△→Y变换：

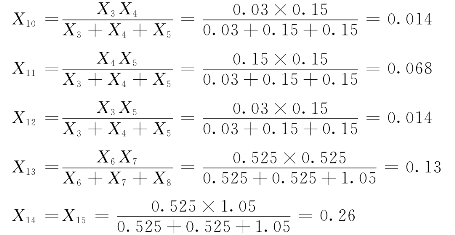
3）串联电抗合并：

X16=0.4+0.33+0.014=0.74

X17=0.014+0.13=0.144

X18=0.264+1.65=1.91

4）Y→△变换：

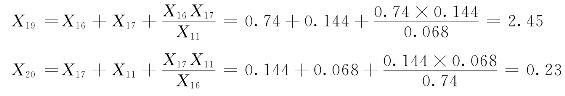
X21连接两个电源，已经与短路点的短路电流无关，不必计算了。

5）星→网变换求出各电源对短路点的“转移电抗”：

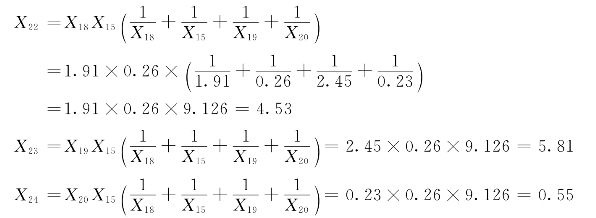
6）将“转移电抗”化为各电源到短路点的“计算电抗”：

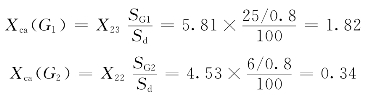
GS代表无穷大电源系统，不能求它的计算电抗。无穷大电源系统要直接用转移电抗X24进行计算。

（3）计算各电源供给的短路电流。有限容量电源根据其计算电抗查运算曲线（本例查汽轮发电机曲线），可求出各个时刻的短路电流标幺值，进而求出其有名值；无穷大电源则根据其转移电抗直接进行计算。

1）电源G1供给在短路点处产生的短路电流：先求以电源G1容量为基准容量、以短路点平均电压为基准电压的电流基准值：

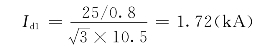
查附录的0s曲线，对应Xca=1.82：

I″*=0.57 I″=0.57×1.72=0.98（kA）

查附录的0.2s曲线，对应Xca=1.82：

查附录的4s曲线，对应Xca=1.82：

2）电源G2供给在短路点处产生的短路电流：求以电源G2容量为基准容量、以短路点平均电压为基准电压的电流基准值：

查附录的0s曲线，对应Xca=0.34：

I″=3.16 I″=3.16×0.41=1.3（kA）

查附录的0.2s曲线，对应Xca=0.34：

查附录的4s曲线，对应Xca=0.34：

3）无穷大电源供给在短路点处产生的短路电流：

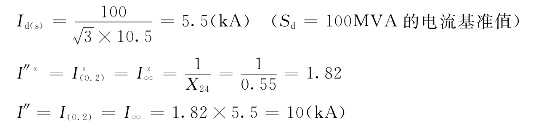
（4）求短路点总的三相短路电流：

I″k=0.98+1.3+10=12.28（kA）Ik（0.2）=0.93+1.03+10=11.96（kA）

Ik∞=1.0+0.94+10=11.94（kA）

（5）求短路点的短路容量：

（6）求三相短路冲击电流（取Ksh=1.8）：

以上就是三相短路电流计算的全过程。

（三）短路电流计算中的几个问题

1.电源的合并问题

当几个电源的类型和容量相近，且各自到短路点的电气距离（即电抗值）相差不大时，可以将它们合并成一个等值电源。等值电源的容量就等于各电源的容量之和，等值电抗则是各电源支路电抗的并联。两个电源的合并，见图7-11。

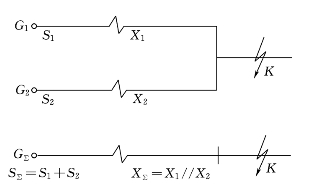
图7-11 两个电源的合并

当两个电源类型不同，或到短路点的电气距离相差很大时，就不可以合并，否则误差就太大了。

一般，可以合并电源的条件是：

式中 S1、S2——两个电源的容量；(www.xing528.com)

X1、X2——两个电源到短路点的等值电抗。

2.短路电流冲击系数Ksh的不同取值

在计算多电源网络中某点短路时，要分别求出各电源供给的冲击短路电流有名值，最后再总加起来。因为各自的冲击系数Ksh是不相同的。

在电网的不同地点短路，冲击系数Ksh取值不同。

在发电机出口短路时，取Ksh=1.9；在发电厂升压变压器高压侧母线短路时，取Ksh=1.85；在高压电网其他地点短路时，取Ksh=1.8；在1000kVA及以下变压器低压侧0.4kV短路时，取Ksh=1.3。

冲击系数Ksh也可由图7-12查得。

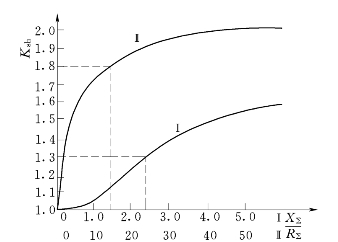
图7-12 短路电流冲击系数Ksh曲线

冲击系数公式为：

Ta为短路回路时间常数，与短路回路参数X∑/R∑有关：

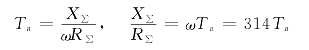
在发电厂以外高压电网中，短路回路时间常数Ta通常约为0.05s，则

X∑/R∑=314×0.05=15.7

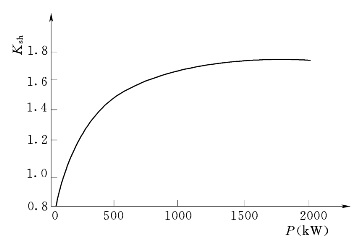
图7-13 异步电动机冲击系数曲线

由图7-12曲线Ⅱ，此时对应的冲击系数Ksh=1.8：

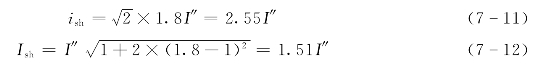
3.对电网中负荷的处理

（1）一般综合负荷。发生短路时，综合负荷的电流会因电压下降而大为减小，与巨大的短路电流相比，完全可略去不计，即认为此刻负荷均从网络中断开，不参与短路电流计算。

（2）异步电动机。异步电动机在稳定运行时，相当于一个阻抗。然而在短路初瞬次暂态时段内，接在短路点附近（一般为5m以内）的较大容量异步电动机（高压电动机容量在800kW以上、低压电动机容量在200kW以上）却类似于一台发电机，也能向短路点反馈次暂态短路电流和冲击短路电流。其等值电路如图7-14所示。

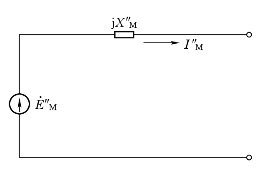
图7-14 短路瞬间异步电动机等效电路

可按下列公式计算：

式中 E″M*——电动机次暂态电势标幺值，一般取0.9（即电动机额定电压的90%）；

X″M*——电动机次暂态电抗标幺值（以本身容量为基准），一般取平均值为0.17（或等于起动电流倍数的倒数，电动机起动电流倍数一般为5～6.5）；

Ksh（M）——电动机短路电流冲击系数，一般估算时，高压电动机可取1.4～1.6，低压电动机可取1.0，也可由图7-13查得；

IMN——电动机额定电流。

在其他情况下，均不考虑异步电动机的反馈电流。

（3）同步电动机和同步调相机。接于系统中某一点上的同步电动机或同步调相机，当容量大于1000kVA时，在短路计算中应看做附加电源，可用运算曲线法计算其供出的短路电流。对同步电动机可查有自动电压调整装置的水轮发电机运算曲线，但查曲线时所用的时间要改为等值时间，即t′=2t（如查0.2s的I0.2，要查0.4s的曲线）。这是由于两者定子开路时励磁绕组的时间常数不同，水轮发电机一般为5s，而同步电动机一般平均值为2.5s。

对同步调相机，可查有自动励磁调节装置的汽轮发电机运算曲线。

4.系统的等值电抗的估算

在计算短路电流时，有时供电部门只给出系统总容量以及某个分界母线处的短路容量，有时则只知道分界母线上的断路器的额定断流容量，这时可用下式估算出系统的等值电抗标幺值：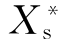

式中 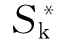——系统中某点短路容量的标幺值；

Sk——系统分界母线处的短路容量（常用该处断路器额定断流容量代替）；

Sd——基准容量，一般取100MVA。

5.短路时母线残压的计算

电网中发生三相短路时，短路点的电压已降为零，短路点邻近地点电压也大为降低。为分析短路时电力系统的运行状态或因继电保护整定计算的要求，常需计算系统中某点在短路时的电压，称为残压，以Ure表示。

稳态短路时系统某点残压（标幺值）的计算按下式进行：

式中 X*——由短路点算起到系统某点的电抗标幺值。

四、不对称短路的计算方法

（一）短路回路中各元件的序电抗

按照对称分量法的观点，当电网中发生不对称短路时，三相短路电流IKA、IKB、IKC是不对称的，因而可以分解成正序分量短路电流、负序分量短路电流和零序分量短路电流。各元件通过各序分量电流时，应分别产生正序分量压降、负序分量压降和零序分量压降。现定义：

正序压降与正序电流之比，称为元件的正序电抗X1。

负序压降与负序电流之比，称为元件的负序电抗X2。

零序压降与零序电流之比，称为元件的零序电抗X0。

元件各序电抗的数值是不同的，分述如下。

1.正序电抗X1

正序电抗X1的数值，即为电网各元件参数计算公式所算得的电抗值。

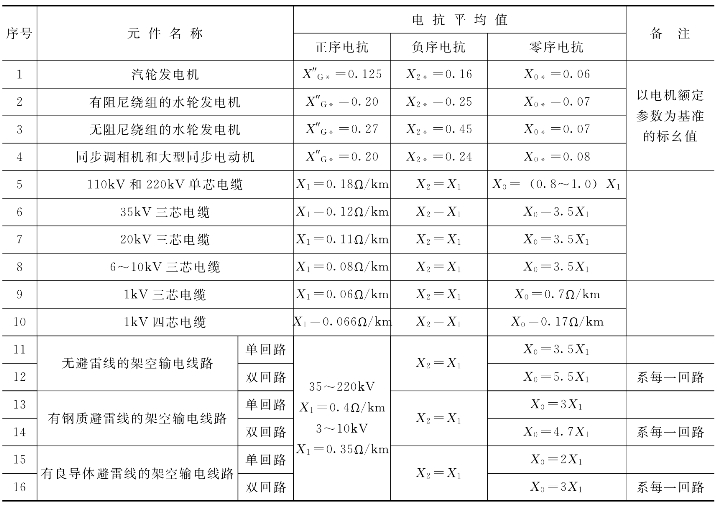
2.负序电抗X2

对于静止的电气设备，如变压器、线路、电抗器等，其负序电抗值与正序电抗值完全相同，即X2=X1；对旋转电机，X2≠X1，一般计算时可采用表7-1中的数值（两者相差并不大，亦可认为X2≈X1）。

3.零序电抗X0

零序电抗的情况比较复杂。零序电流从短路点出发，由于三相电路的零序电流相位相同，如果前方变压器的绕组中性点没有接地（△或Y），零序电流就不能流通，相当于该变压器的零序电抗为无穷大。因此零序电抗与电网中性点是否接地以及其他许多因素密切相关，要分别加以说明：

（1）架空及电缆线路的零序电抗比正序电抗大许多，与许多因素有关，可查表7-2。

（2）同步电机的零序电抗比正序电抗小，一般常取表7-2中的数值。

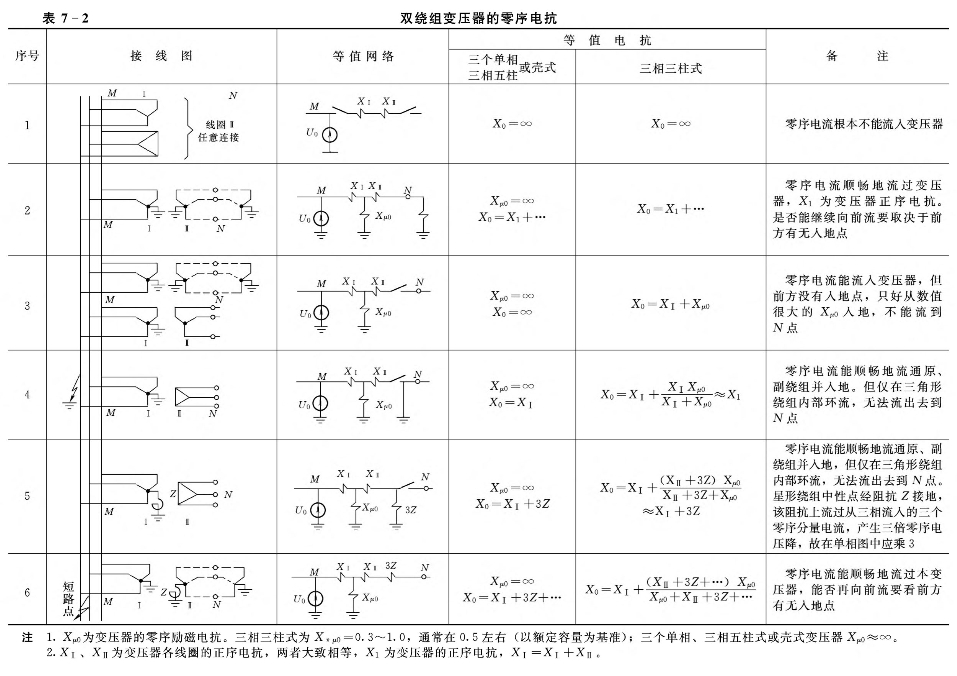
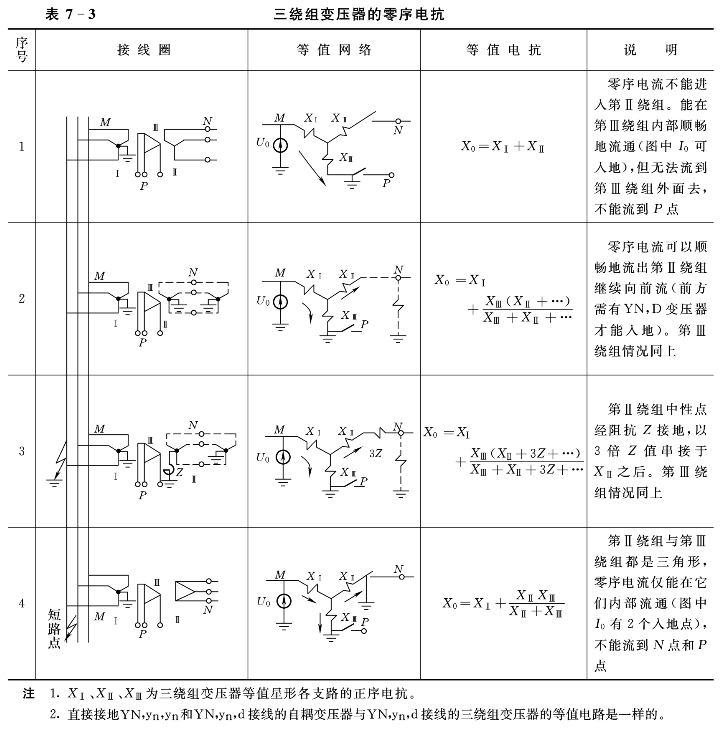
（3）变压器的零序电抗，当零序电流可以顺畅地流通时，就等于其正序电抗；当零序电流不能顺畅地流通时，则可近似认为X0=∞。具体情形可见表7-2和表7-3。

（二）不对称短路时的序网图

发生不对称短路时，可以认为各序电流分别流经各自的序网。

1.正序网络

正序网络就是前面三相短路计算时所用的等值电路，电源的参数和电抗的参数都没有变动。实际上，可以把三相短路看作不对称短路的特例：只有正序电流流经正序网络，而没有负序电流（流经负序网）和零序电流（流经零序网）。对正序网的求解也完全与前面三相短路电流计算方法相同。

2.负序网络

负序网络与正序网络仅有两点不同：

（1）所有元件的电抗都用负序电抗X2。实际上，对不旋转的静止元件，X2=X1。只有旋转电机，X2稍大于X1。当无详细资料时，也可近似采用X2=X1。

（2）负序网络中原来的电源没有了（因为这些电源也属于正序），而是将电源点接地。推动负序电流流动的负序电压是作用在短路点处。即负序电流是从短路点流出，最后从接地点（即原来电源点）入地返回。

3.零序网络

零序网络与正序、负序网络差别很大。推动零序电流的零序电压，也是作用于短路点处。零序电流从短路点出发，遇到线路、电抗器以及YN，yn接法的变压器时，都可以顺畅地流过去（但注意各元件要采用其零序电抗）。而遇到Y，y接法、Y，yn接法、D，y接法或D，yn接法的变压器时则不能流通一般情况下均可认为变压器激磁电抗Xμ0为无穷大。最后只有流经YN，d（即Y/Δ）接法的变压器才能够流入“地”，完成零序电流的闭合回路。如果变压器中性点是经过阻抗而接地的，则须将此阻抗值乘3后串接在零序电流回路中。凡没有流通零序电流的各个元件，均不出现在零序网络中。

表7-1 各种元件的各序电抗平均值

（三）序网络的化简和各序的综合电抗

各序网络均可化简为一个综合电抗。

正序网络一般有多个电源点，可先按三相短路计算方法求得各电源对短路点的转移电抗，然后将各电源支路合并为一个等值电源（不必计算等值电势值）和一个等值电抗，这个等值电抗就是正序综合电抗，用X1∑表示。但如果各电源容量相差很大，就不要进行合并，还是分别计算各电源供出的短路电流为宜。

负序网络和零序网络都只有一个电源点（即短路点），另有多个接地点。负序网络的接地点是各个电源点；零序网络的接地点则是各个接法为YN，d的变压器。

从短路点看出去，对各支路进行合并化简，最后就可以化简为一个位于电源点（短路点）和“地”之间的综合电抗，即负序综合电抗X2∑和零序综合电抗X0∑。实际上，在多数情况下，X2∑≈X1∑，而一般X0∑＞X1∑。

（四）利用正序增广网络求解不对称短路

可以利用正序增广网络求解不对称短路。即在正序网络化简到各电源点到短路点仅为转移电抗时，在原来短路点K处插入一个附加电抗XΔ后再短路接地。此附加电抗与短路类型有关，见表7-4。

新接地点处可称为K′，然后再重新求各电源点到新接地点K′点的转移电抗，再用前述求三相短路同样的方法，求得各电源点对K′处三相短路时供出的短路电流，该电流也就是在K处不对称短路时，短路电流中的正序分量。

最后，正序分量再乘以一个与短路类型有关的故障电流系数m（见表7-4），就最终求得发生K点不对称短路时，故障点的实际短路电流。这称为正序增广法则。详见例7-4。

表7-4 各种短路的附加电抗XΔ和故障电流系数m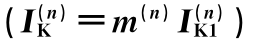

图7-15绘出了各种短路时的正序增广网络图。

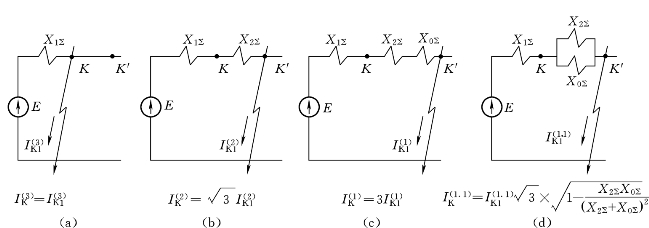
图7-15 各种短路时的正序增广网络图

（a）三相短路时（无任何变化，XΔ=0，m=1）；（b）二相短路时（K→K′，XΔ=X2∑，m=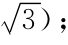；（c）单相短路时（K→K′，XΔ=X2∑+X0∑，m=3）；（d）两相短路接地时

（五）和三相短路的比较

1.两相短路与三相短路的比较

由图7-15（a）可见：

式中 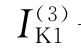——三相短路电流的正序分量，也就等于三相短路电流本身；

E——电源电势（经合并以后的总电源），实用计算中其标幺值可取1.0；

X1∑——正序综合电抗。

由图7-15（b）可见：

式中 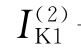——两相短路电流的正序分量。

因而有：

这是一个很有用的结论，即：在由无穷大系统供电时，两相短路电流总是小于同一点三相短路电流，为三相短路电流的86.6%。

2.单相短路与三相短路的比较

假设零序电抗近似与正序、负序电抗相等，X0∑≈X1∑≈X2∑，由图7-15（c）可知：

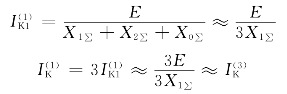
可见这时单相短路电流等于三相短路电流。

实际上，X0∑往往大于X1∑，因此一般而言单相短路电流小于同一点的三相短路电流。但也可能出现X0∑＜X1∑的个别情况，此时单相短路电流就大于三相短路电流了。X0∑的大小可以用改变系统中性点接地的数量和分布来进行调控，一般应使X0∑＞X1∑，以避免出现的情况。

【例7-4】 如图7-16所示之电网，有关参数已注明，求图中K点发生各种短路时的短路电流（输电线路X1=0.4Ω/km，X0=3X1）。

图7-16 不对称短路计算的原始网络图

解 取Sd=100MVA，Ud=Uav。

（1）各序网及参数计算（为简便计，略去“序”的下标及标幺值的“*”号）

1）原始网络等值电路（标幺值），见图7-17。

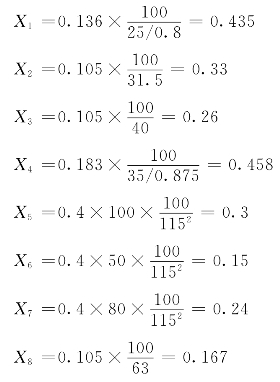
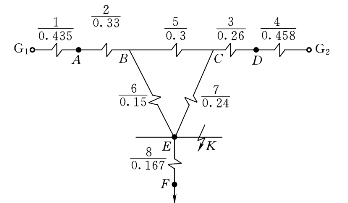
图7-17 原始网络的等值电路图（标幺值）

2）正序网络及其化简，见图7-18。

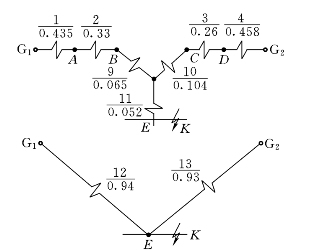
图7-18 正序网络及其化简

X8=0.167（但因是负荷支路，可断开，在正序网络中不画了）

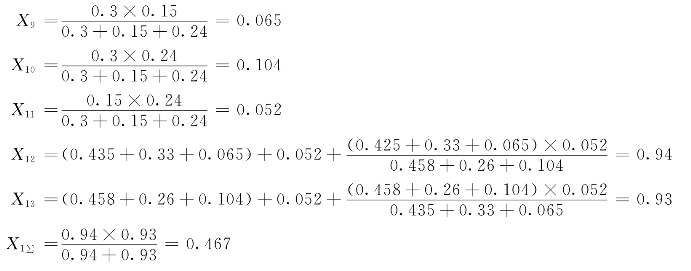
3）负序网络及其化简，G1及G2处接地，见图7-19。

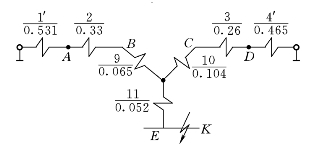
图7-19 负序网络及其化简

4）零序网络及其化简（A点、D点及F点三处接地，见图7-20）

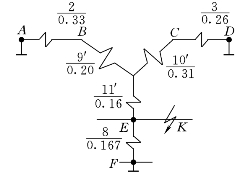
图7-20 零序网络及其化简

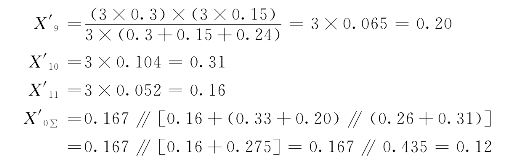
（2）K点发生单相短路的短路电流。单相短路时的附加电抗：

作出正序增广网络，并化简成各电源到新的短路点K′的转移电抗（参见图7-21），再求出火电厂和水电厂到新短路点K′的计算电抗：

查运算曲线或查表（0s）得到短路电流标幺值，进而求出其有名值：

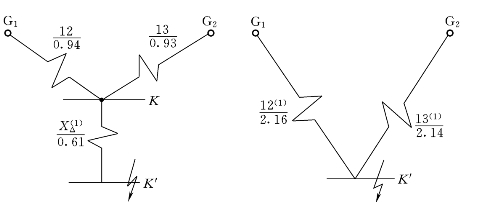
图7-21 单相短路时的正序增广网络及其化简

这是在K′点发生三相短路时各电厂供出流到短路点的电流，也是在原K点发生单相短路时，各电厂供给短路点短路电流中的正序分量，乘以故障电流系数m（1）=3以后，才是在K点发生单相短路时，短路点的实际故障电流：

（3）K点发生二相短路时的短路电流。二相短路时的附加电抗：

作出正序增广网络（见图7-22），求到K′的转移电抗和计算电抗：

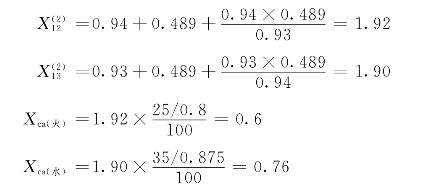
查运算曲线或查表（0s）得到短路电流的标幺值，进而求出其有名值：

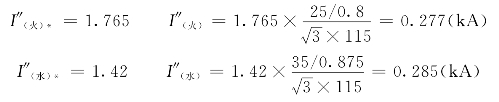
二相短路故障电流系数K点二相短路故障点的实际短路电流为：

（4）K点发生二相短路接地时的短路电流

二相短路接地时的附加电抗：

作出正序增广网络（见图7-23），求到K′的转移电抗和计算电抗：

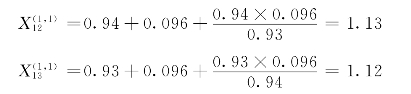
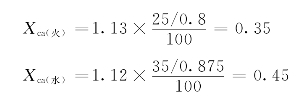
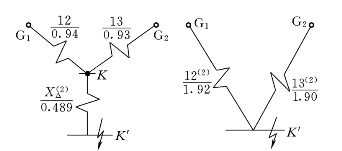
图7-22 两相短路时的正序增广网络及其化简图

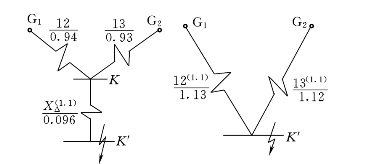
图7-23 两相短路接地时的正序增广网络及其化简图

查运算曲线或查表（0s）得到短路电流的标幺值，进而求出其有名值：

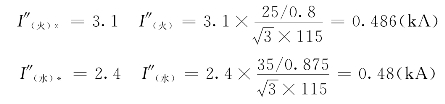
二相短路接地时故障电流系数：

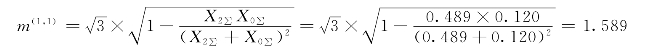
K点二相短路接地时故障点的实际短路电流为：

I″（1，1）=1.589×（0.486+0.48）=1.535（kA）

（5）K点发生三相短路时的短路电流。三相短路时附加电抗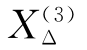=0。因此不需增广，直接由到K点的转移电抗X12、X13求计算电抗。

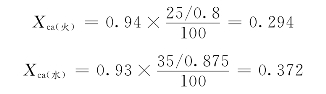
查运算曲线或查表（0s）得到短路电流的标幺值，进而求出其有名值：

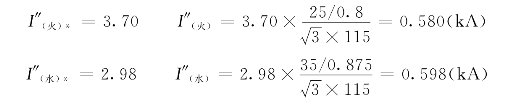
三相短路时故障电流系数m=1，火电厂和水电厂供给短路点的短路电流相加：

I″（3）=0.580+0.598=1.18（kA）

本例中只计算了0s时刻的短路电流I″，同样可查运算曲线得到任意时刻的短路电流。由本例可见，用正序增广网络方法求各种不对称短路非常简便。

在本例中

X1∑=0.467

X2∑=0.489

X0∑=0.12

可见，X2∑略大于X1∑，近似认为X2∑=X1∑也是可以的。而X0∑却没能大于X1∑，因此使单相短路电流（1.5kA）大于同一点的三相短路电流（1.18kA）。如果打开负荷支路63MVA变压器中性接地刀闸，则零序网络中就去掉了经8号电抗接地的并联支路，此时X0∑=0.435，变大许多，单相短路电流也就会相应减少。

由于本例中不是无限大电源系统供电，两相短路电流（0.974kA）仅为三相短路电流（1.18kA）的82.5%，这个结果是正确的。