【摘要】：交流电抗器类电源都具有图2-10所示的外观像椭圆的VAC。这种VAC曲线属于非线性二次曲线，是椭圆方程，在第一象限，即电压US与电流IS为坐标轴的象限的图像。式（2-6）是正弦量的矢量表达式，将其变换成标量式时，就有：式（2-7）中，US0和XL是常数，可将式（2-7）改变为：式（2-8）正是一个椭圆方程的二次函数表达式。由于负电压US与负电流IS没有意义，所以，式（2-8）表示的是第一象限内电源的VAC曲线。
交流电抗器类电源都具有图2-10所示的外观像椭圆的VAC。在电弧焊工艺中，常称为“陡降特性”。这种VAC曲线属于非线性二次曲线，是椭圆方程，在第一象限，即电压US与电流IS为坐标轴的象限的图像。下面，分析交流电抗器类电源产生这种椭圆形状VAC的原因。
所有交流电抗器类电源，其等值电路都可以用图2-10中所示电路表示。图中，U1是电网电压；US0是变压器T的二次电压，也是变压器的空载电压；L是电抗器，UL是电流流过电抗器时产生的电压降；IS是电源输出电流；US是输出电压。
需要强调指出的是：由于交流电抗器电源工作于50Hz的工频电压下，上述所有参数都按正弦量的矢量表示，而且由正弦量的电路规律所确定。
图2-10 电抗器类电源的基本结构与椭圆伏-安特性
对图2-10所示等值电路，可以按克希荷夫定律得出：
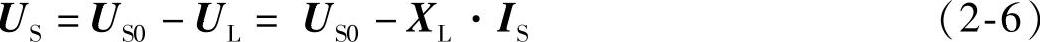(www.xing528.com)
式中 XL——电感L的电抗，XL=2πfL。
式（2-6）是正弦量的矢量表达式，将其变换成标量式时，就有：
式（2-7）中，US0和XL是常数，可将式（2-7）改变为：
式（2-8）正是一个椭圆方程的二次函数表达式。由于负电压US与负电流IS没有意义，所以，式（2-8）表示的是第一象限内电源的VAC曲线。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
