工程重点剖面二维地应力场的概化

重点剖面二维地应力场概化采用弹性平面问题的应力函数方法。由于所应用的理论要求岩体要符合弹性介质假设，在应用上有一定局限性，但对重点剖面上特定的较小范围（无断层和地质构造），这种二维地应力场的概化方法，还是适用的。

在弹性平面问题中，对于常体力的情况，求解应力边界问题时，应力分量σy，σz，τyz应当满足平衡微分方程和相容方程

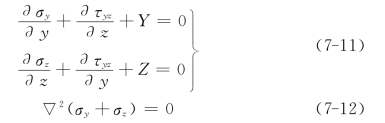
同时在边界上满足应力边界条件

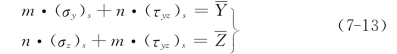
式中：Y，Z为体力分量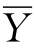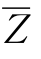；，为在边界上作用的面力分量；m，n为边界法向的方向余弦。

平衡微分方程（7-11）是一个非齐次微分方程组，它的解答包含两个部分，即任一特解和齐次微分方程组通解的叠加。

特解可取为［32］

对于有重力作用的岩体，体力分量Y=0，Z=γ。

齐次微分方程组的通解，可由应力函数φ（y，z）给出

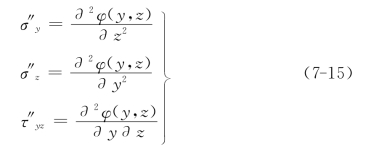
将通解式（7-15）和特解式（7-14）叠加，即得微分方程组（7-11）的全解

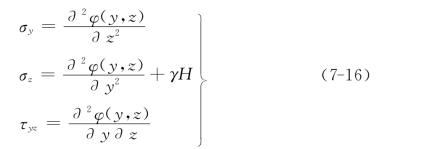
式中：γH为常体积力。

应力分量式（7-16）也必须满足相容方程，代入式（7-12）即得双调和方程

因此，弹性平面问题归结为寻求满足应力边界条件的双调和函数φ（y，z）。

由于双调和方程（7-17）是偏微分方程，它的通解不能写成有限项数形式，不能直接求解，只能采用逆解法或半逆解法求解。

设纵剖面上二维应力分量σy、σz和τyz为坐标的二次函数，则应力函数φ（y，z）为坐标的四次函数，即可表示为

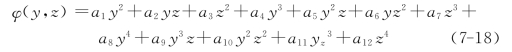
式中：ai（i=1～12）为坐标系数。

应力函数φ（y，z）必须满足双调和方程▽4φ（y，z）=0，因此(www.xing528.com)

根据式（7-16），导出纵剖面上应力分量为

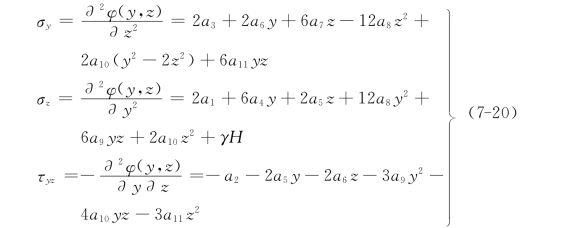
应力分量σy、σz和τyz以ai（i=1～11）作为变量表示为

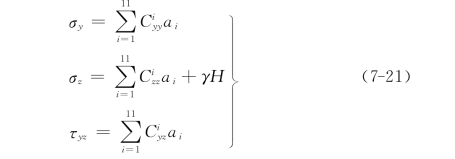
系数列于表7-1。

表7-1　坐标系数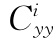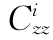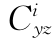，，表

应力函数φ（y，z）的坐标系数ai（i=1～11）必须满足应力观测点和边界观测点的边界条件：

设为应力观测点j的已知应力分量，满足应力观测点的边界条件为

则N1个应力观测点的方差总和

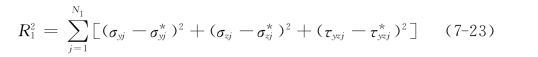
设σn和τn为地表上法向应力和剪应力，αk为地表观测点k法线方向的倾角，满足地表观测点的边界条件为

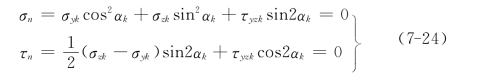
则N2个地表观测点的方差总和

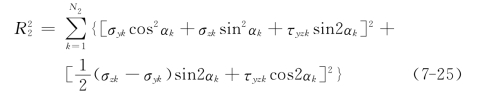
把式（7-21）代入式（7-23）和式（7-25）然后相加，得到全部N1+N2个观测点的方差总和。利用最小二乘法原理，使方差总和为最小，也即对ai取偏导并令其为零

这样可列出11个正规方程，求解11个坐标系数ai（i=1～11）：

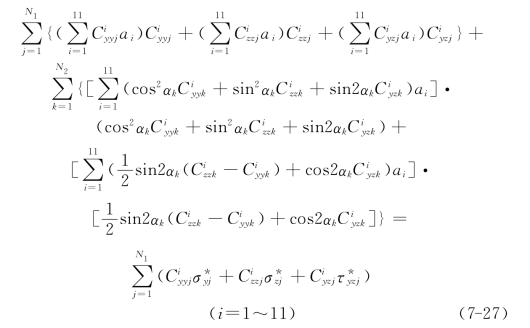
每个应力观测点测得3个应力分量，代入式（7-22）可得3个观测值方程，每个地表观测点，法向应力和剪应力为零，代入式（7-24）可得2个观测值方程，只要3 N1+2 N2＞11，方程组（7-27）就有解。求得待定常数ai以后，应力函数式（7-18）被完全确定，也即剖面上的应力分量σy、σz和τyz根据式（7-21）被完全确定。