应力场回归计算方法优化

在二维地应力场分析中，回归元素定为3个，为自重应力引起的应力场，均匀分布和三角形分布构造应力引起的应力场；在三维地应力场分析中，如果模拟地质构造应力场为主压应力和次压应力情况，回归元素也定为3个：自重应力引起的应力场，地质构造应力场的主压应力和次压应力引起的应力场；如果模拟地质构造应力场为一般应力状态情况，回归元素定为4个：自重应力引起的应力场和地质构造应力场的3个应力分量引起的应力场。为叙述方便仍把回归元素定为3个，回归元素定为4个情况推而知之。

把地应力回归计算值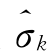作为因变量，把有限元计算求得的自重应力场和地质构造应力场相应于实测点的应力计算值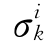作为自变量，则回归方程的形式为

式中：k为观测点的序号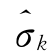；为第k观测点的回归计算值；Li为相应于自变量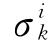的多元回归系数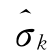；和为相应应力分量计算值的单列矩阵。

坐标轴规定：对二维地应力场分析，轴y为计算剖面走向，轴z为铅垂向上方向；对三维地应力场分析，轴x和轴y为计算域水平边界方向，轴z为铅垂向上方向。

对每一个应力状态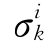可确定一个回归计算值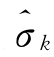。观测值与回归方程的偏离程度，用该观测值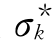与回归计算值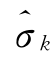之差，即该观测值的残差表示。全部观测值与回归方程的偏离程度，用全部观测值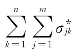与回归计算值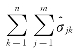的残差平方和表示，即

式中：k为观测点序号；n为观测点的个数，n=n1+n2，n1为三维地应力测点（套钻孔应力解除法测量）的个数，n2为二维地应力测点（水压致裂法测量）的个数，二维地应力测点编列在三维地应力测点后面；j为应力分量序号；m为应力分量的个数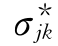；为第k观测点序号为j应力分量实测值，例如。对二维地应力场分析，当k≤n1时，m=3，当k＞n1时，m=1；对三维地应力场分析，当k≤n1时，m=6，当k＞n1时，m=3。(www.xing528.com)

采用数理统计的最小二乘法原理，使残差平方和为最小，即式（7-2）对Li取偏导并令其为零，得到求解回归系数Li的正规方程组［85］［86］

解得回归系数Li（i=1～3）以后，就可根据回归方程和有限元计算结果求得计算域内各处的应力回归计算值。

应力回归的效果，依照回归方程和回归元素的显著性检验值F和Fi进行 检验：

式中：Rv和R为回归差平方和和残差平方和，N为回归差平方和的自由度，Vi为回归方程中各自变量的贡献，用变量的偏回归差平方和表示：

式中：Cii为正规方程组（7-3）系数矩阵逆阵的主元素。