工程应用实例：三峡工程船闸区8号勘探平洞位移反分析计算

1）位移监测的数学计算模型和求解

为研究三峡工程原拟定的船闸区陡高边坡稳定性和围岩变形特性，长江科学院于1986年在8号勘探平洞4号支洞开展围岩位移监测试验。4号支洞位于8号勘探平洞洞深249.5m的右壁，洞向107°，支洞断面为宽4m、高3m、边墙高2.5m的圆拱直墙型洞室，长30.5m，上覆岩层厚度约60m。共布置两个围岩变形观测断面，分别布置在支洞深9m和20.1m处。对位移监测资料进行分析，舍弃了一部分不合理位移观测值。观测值选用的评判标准为：各观测值的合理性与随时间变化的稳定性；同一钻孔不同测深观测值的协调性；相邻钻孔相近测深观测值的可对比性。位移反分析计算所采用的位移观测值为下列钻孔测点所获得的观测数据：第一断面右边墙水平钻孔深度为2m、3m、6m测点和拱顶铅垂钻孔深度为1m、5.7m测点，第二观测断面左边墙水平钻孔深度为3m、4m、6m测点。它们与开挖深度关系曲线如图5-5所示。

计算所需的岩体弹性常数，取用岩体变形模量和泊桑比为E=39.23GPa，μ=0.22。

有限元计算方法的计算网格如图5-6，计算模型为四周外边界全约束，洞室周边内边界施加由式（5-4）表达的三种单位岩体初始应力所产生的等效节点释放力，有限元计算以后按式（5-5）建立观测值方程组，然后求解。

复变函数计算方法首先按式（5-16）和式（5-39）求得地下洞室实际平面z映射到单位圆孔的无限平面ζ的映射函数

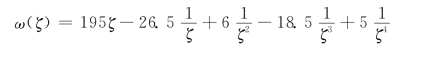
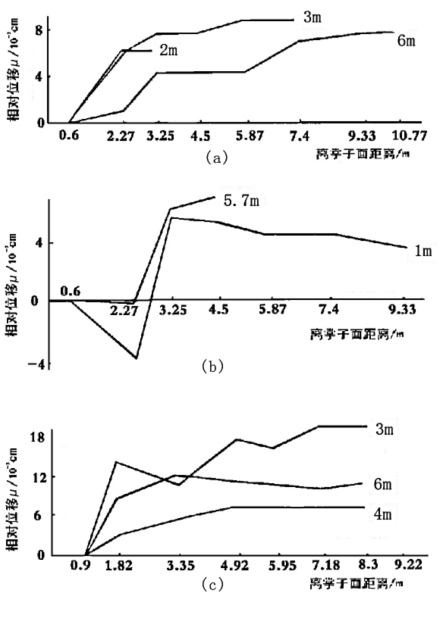
图5-5　位移—距离实测曲线

（a）右边墙水平孔 （b）拱顶铅垂孔 （c）左边墙水平孔

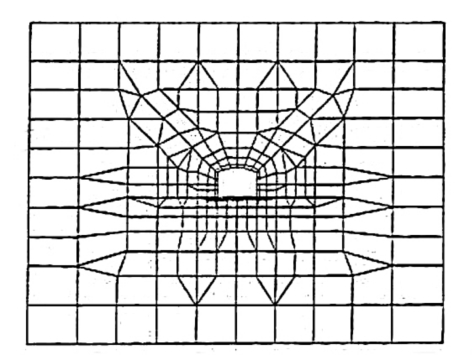
图5-6　有限元计算法的计算网格

映射函数边界与实际边界一起绘于图5-7，由图5-7可知两者非常接近，最大差值在拱座处仅20cm。

钻孔多点位移计水平测孔孔口离平洞底板约1.4m，映射平面圆心相对应实际平面的位置离平洞底板1.39m。因此实际平面上钻孔多点位移计水平向测孔和铅垂向测孔正好与映射平面上通过圆心的水平轴和垂直轴相对应，这样就无需再寻找钻孔多点位移计水平向测

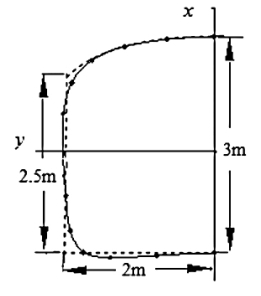
图5-7　映射函数边界和实际边界的比较

孔和铅垂向测孔各测点相对应的极径方向（各测点相对应的极径方向就是水平向和铅垂向）。按实际平面测点坐标求得映射平面相应测点的映射点坐标，根据式（5-19）进行数值计算以后，再按式（5-48）建立观测值方程组，然后按（5-49）求解。

2）两种计算方法与岩体初始应力实测值的比较

1989年10—11月在仅离4号支洞左壁12m的3号支洞（洞向105°）内，采用平洞浅钻孔三向应变计进行岩体初始应力测量，测量钻孔为两个水平孔，布置在支洞洞深16.95m和19.80m（4号支洞第二位移观测断面的相应深度）的左壁，测量深度为7.33～10.76m。两种位移反分析计算方法所得的岩体初始应力计算值和相应断面的3号支洞岩体初始应力实测值一起列于表5-1。由表5-1可知，有限元和复变函数两种反分析计算方法所获得的岩体初始应力计算值与相应断面的3号支洞岩体初始应力实测值都非常吻合，应力分量和主应力计算值与相应实测值的平均相对差值的绝对值仅为0.30MPa、0.30MPa和0.36MPa、0.39MPa，主应力方向仅差12.8°和0.85°。

3）两种计算方法成果的比较(www.xing528.com)

由表5-1可知，两种反分析计算方法所获得的岩体初始应力计算值非常接近，应力分量和主应力量值绝对值的平均相对差值仅为0.44MPa和0.55MPa，平均仅占大主应力的9.55%和11.94%，主应力方向相对差仅为4.4°。

表5-1　岩体初始应力计算值与实测值的比较

4）测线上相对位移计算值与观测值的比较

两种位移反分析计算所得的测线上相对位移计算值与观测值列于表5-2。由表5-2可知，两种反分析计算方法所获得的测线上相对位移计算值是非常接近的，平均相对差值仅为0.85×10-3cm，仅占最大位移计算值的3.9%。

表5-2　测线上相对位移计算值与观测值的比较（×10-3cm）

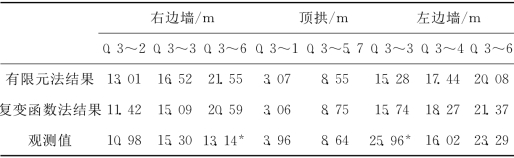
两种反分析计算方法所获得的测线上相对位移计算值与观测值也是非常吻合的。除了右边墙水平孔0.3～6m测线和左边墙水平孔0.3～3m测线（这两个观测值与同钻孔其他测线上观测值偏离太远，很不协调，在实际反分析计算中被舍弃，表中右上角带“＊”者）相对差值较大外，其余都比较小。除了这两测线上观测值外，其余测线上相对位移计算值与观测值的平均相对差值，有限元计算法为1.48×10-3cm，复变函数数值计算法为0.97×10-3cm。

5）围岩应力场和位移场分析

位移反分析的目的不仅要反演造成此位移场的岩体初始应力场，还要对在此岩体初始应力场作用下围岩的应力场和位移场进行分析。

（1）洞室岩壁应力和位移分布规律。两种位移反分析计算获得的洞室岩壁围岩切向应力和位移分布如图5-8所示。由图5-8可知，不同方法计算所得的洞室岩壁切向应力和位移在大部分岩壁上是非常接近的，获得了基本一致的结果，拱顶的岩壁切向应力和位移几乎完全一致，两者仅差0.68%和2.97%。洞室最大岩壁切向应力都发生在右边墙上部，其次在左边墙下部。最大岩壁切向应力，有限元法为9.73MPa，复变函数法为10.86MPa，顶拱岩壁切向应力较均匀，且无拉应力区域，是一种比较稳定的围岩应力分布。最大岩壁位移，有限元法为30.85×10-3cm，复变函数法为33.82×10-3cm，顶拱岩壁位移量较小，也是一种比较稳定的围岩位移分布。

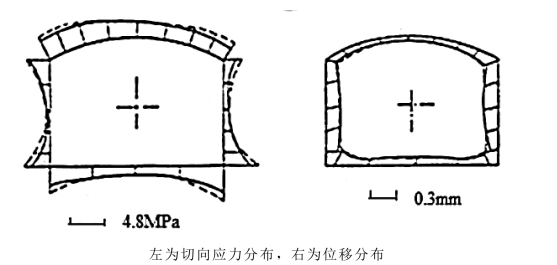
图5-8　两种方法计算所得的岩壁切向应力和位移分布的比较

两种位移反分析计算方法所获得的结果，在边墙墙脚和拱顶转角处相差稍大，尤其在拱座附近，并且岩壁切向应力和位移有限元法结果普遍要比复变函数法结果小一些，它们沿岩壁的分布图形，有限元法结果比复变函数法结果更显得歪扭。产生这种现象的原因是：由于计算方法不同，洞室岩壁转角处，有限元法并不像复变函数法那样造成很大的应力集中；另外有限元法反分析计算获得的岩体初始应力要比复变函数法计算稍小一些（尤其是小主应力），而剪应力分量要稍大一些。

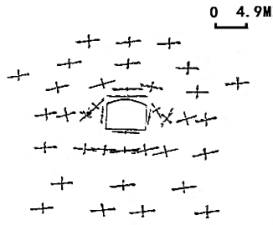
图5-9　两种方法计算所得的围岩内部应力状态的比较

（2）围岩内部应力分布状态。两种位移反分析计算获得的围岩内部应力状态分布如图5-9所示，沿拱顶铅垂线上岩体应力分量的分布如图5-10所示。由图5-9可知，不同方法计算得到的围岩内部应力状态是非常一致的。根据围岩内部39个节点的统计，主应力量值，有限元法计算结果都比复变函数法计算结果稍小一些，而主应力方向两种方法的计算结果平均仅差4.85°，绝大部分有限元法比复变函数法稍大一些。同时由图5-10可知，拱顶铅垂线上岩体正应力分量，有限元法计算结果比复变函数法计算结果稍小一些，而剪应力分量，有限元法计算结果比复变函数法计算结果稍大一些，产生这种现象的原因也是由于有限元法反分析计算所获得的岩体初始应力要比复变函数法计算结果稍小一些，而剪应力分量要稍大一些之故。

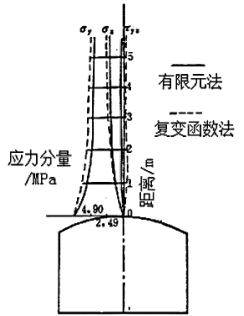
图5-10　两种计算方法所获得的拱顶铅垂线上应力分量的比较