5.1.2.1 弹性平面问题复变函数解法的基本公式[15]
弹性平面问题归结为寻求满足边界条件
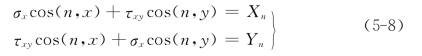
和双调和方程
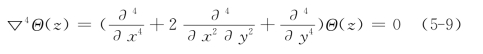
的应力函数Θ(z),式中,Xn,Yn为作用在边界上外力主矢量的分量,n为边界的外法线方向。
应力函数Θ(z)可用复变函数表示,由两个正则函数φ1(z)和x1(z)组成
![]()
于是用复变函数表示的位移分量和应力分量公式为
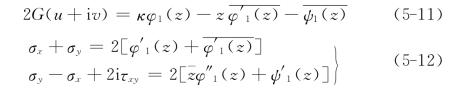
对于无限域,复变函数φ1(z)和xi(z)有

式中:X和Y为边界上外应力主矢量,对目前问题X=Y=0,对平面应变问题κ=3-4μ(μ为岩石泊松比)。 (z)和
(z)和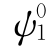 (z)为在边界外包括无穷远点在内的全纯函数,在已给定的应力情况下有如下形式
(z)为在边界外包括无穷远点在内的全纯函数,在已给定的应力情况下有如下形式
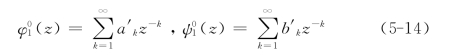
Γ和Γ′为无穷远处应力状态,设σ1和σ2为无穷远处大、小主应力,以压应力为正,α为σ1与轴x逆时针向夹角,则

对于非圆形地下洞室利用映射函数z=ω(ζ)把所研究的非圆形洞室的无限平面z,映射到带有单位圆孔洞的无限平面ζ上,其映射函数为一无穷级数,其形式为
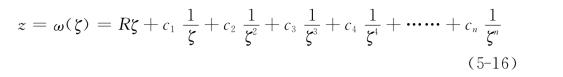
式中:R,c1,c2,c3,c4,…和cn为待定常数,由洞室的边界条件确定。
将式(5-16)代入式(5-13)和式(5-14),则得到平面ζ上复变函数
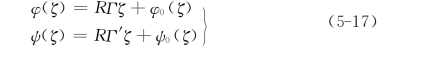
式中:
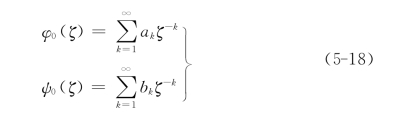
这时位移分量公式(5-11)和应力公式(5-12)变成
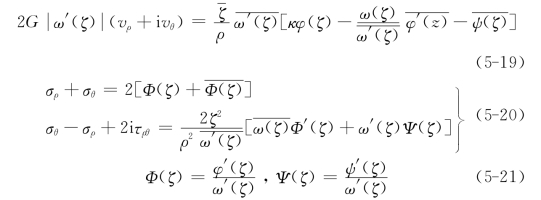
解题的边界条件为
![]()
式中:t为平面ζ上的边界值(t=eiθ),而目前情况Xn=Yn=0,即f=i∫l(Xn+i Yn)ds=0,把式(5-17)代入得
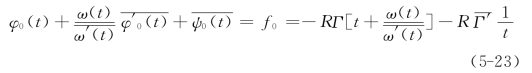
因此,按边界条件式(5-23)进行求解,得到复变函数φ0(ζ)和ψ0(ζ),也即得到复变函数φ(ζ)和ψ(ζ)。
具体分析边界条件式(5-23),根据映射函数式(5-16),式中右边第二项中![]() 总可以表示为
总可以表示为
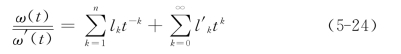
而φ0(t)是在单位圆外无限域全纯函数φ0(ζ)的边界值,t-1是无限域全纯函数ζ-1的边界值,而![]() 和
和![]() 是函数
是函数![]() 和
和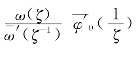 的边界值,在无限域全纯只有
的边界值,在无限域全纯只有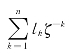 和
和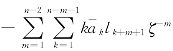 ,这些函数在无限域中的柯西积分为该全纯函数的负值(因φ0(∞)=0)。边界条件式(5-23)的其余两项,其函数在无限域不全纯,柯西积分为零。因此得到复变函数φ0(t)为
,这些函数在无限域中的柯西积分为该全纯函数的负值(因φ0(∞)=0)。边界条件式(5-23)的其余两项,其函数在无限域不全纯,柯西积分为零。因此得到复变函数φ0(t)为
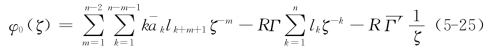
比较等式左右两边各幂次项系数,即可建立解复变函数φ0(ζ)系数a1,a2,…,an的联立方程。
将边界条件式(5-23)取共轭
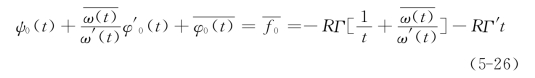
式中:![]() 和
和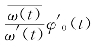 是
是![]() 和
和![]() 的边界值,其共轭函数
的边界值,其共轭函数![]() 和
和![]() 在无限域全纯函数为
在无限域全纯函数为![]() 和
和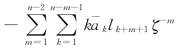 ,因 此 函 数
,因 此 函 数![]() 和
和![]() 在 无 限 域 全 纯 函 数 为
在 无 限 域 全 纯 函 数 为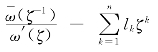 和
和![]() ,这样,根据柯西积分得到复变函数ψ0(ζ)为[17][18]
,这样,根据柯西积分得到复变函数ψ0(ζ)为[17][18]
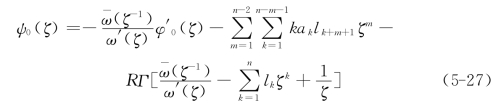
比较式(5-25)得到
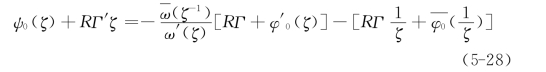
也即复变函数ψ(ζ)可用复变函数φ(ζ)表示,即
![]()
实际工程中映射函数取5项已达到足够精度,即n=4(式(5-16)中ζ的负幂次项取到4次项),复变函数φ0(ζ)由式(5-25)可表示为
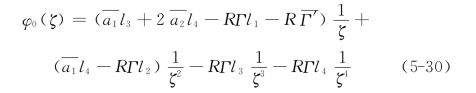 (https://www.xing528.com)
(https://www.xing528.com)
式中:l1,l2,l3和l4根据式(5-24)简单运算后求得,这时式(5-24)可写成
![]()
得到[19][71]
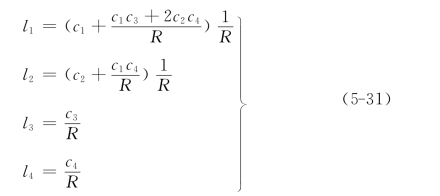
比较式(5-30)等式左右两边各幂次项系数,建立求解系数a1,a2,a3和a4的联立方程组,解此方程组,并注意到式(5-15)和式(5-31),就可得到复变函数φ0(ζ)的各项系数,其中a1和a2为复数形式,a3和a4为实数形式,设
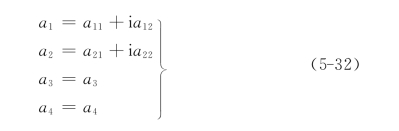
其中:
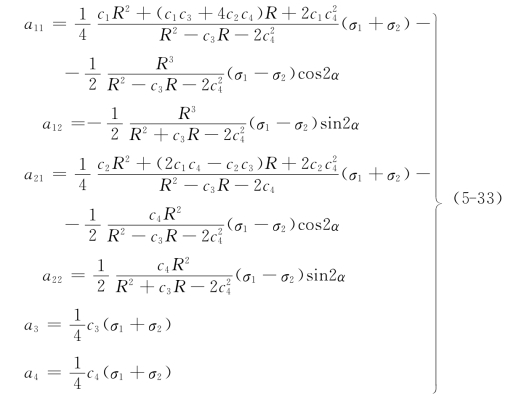
求得复变函数φ0(ζ)和ψ0(ζ)以后,也即求得复变函数φ(ζ)和ψ(ζ),再代入式(5-19)和式(5-20),就可得到欲求的位移分量和应力分量。
5.1.2.2 映射函数的推求[71]
推求映射函数,也即推求式(5-16)的待定常数R、c1、c2、c3和c4,有学者采用对实际边界积分方法,但计算工作量很大。本章采用对实际边界的几个控制点限定方法,建立控制点方程组,然后解题获得,简捷又方便。
实际平面z映射到单位圆映射平面ζ,它们的边界点是一一对应的。设映射平面ζ的边界点为t,t=eiθ=cosθ+i sinθ,相对应的实际平面z(z=x+i y)的边界点坐标为
x=(R+c1)cosθ+c2cos2θ+c3cos3θ+c4cos4θ
y=(R-c1)sinθ-c2sin2θ-c3sin3θ-c4sin4θ
设地下洞室高为h,直边墙高为h1,半跨为l。由于沿纵轴对称,取其一半图形,并设轴x为铅垂向上方向,轴y为水平向左方向,参阅图5-2所示,把映射平面ζ的边界(单位圆)圆周角(0°~180°)等分若干份,其间隔为θ1。5个待定常数需要在实际平面z的边界上寻找5个控制点建立5个边界控制点方程,然后联立解题。
(1)在拱顶(θ=0°)和底板中点(θ=180°)上,x|θ=0-x|θ=180°=h:
x|θ=0°=R+c1+c2+c3+c4
x|θ=180°=-R-c1+c2-c3+c4

图5-2 映射函数边界(实线)和地下洞室边界(虚线)
得 ![]()
(2)在直边墙中部附近节点(θ=90°)上,y|θ=90°=l:
y|θ=90°=R-c1+c3
得 ![]()
(3)在直边墙邻近y|θ=90°上下两节点(θ=90°-θ1和θ=90°+θ1)上,![]() :
:
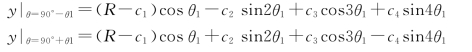
作简单运算![]() 和
和![]() =0
=0
得 ![]()
![]()
(4)在 直 边 墙 邻 近y|θ=90°下 第 二 节 点(θ=90°+2θ1)上,y|θ=90°+2θ1=l:
![]()
得 ![]()
作为校核用,在底板中点x|θ=180°右一节点(θ=180°-θ1)上,![]()
![]()
得 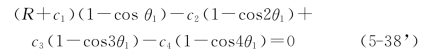
联立方程式(5-34)~式(5-38)解题得到:
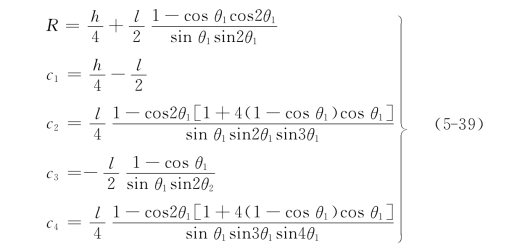
即得到映射函数ω(ζ)(式(5-16)取5项)。
根据映射函数表达式(5-16)求得的映射平面ζ单位圆圆心在实际平面z的对应点后,可求得实际平面z监测点(z=x+i y)对应于映射平面ζ的坐标(ζ=ρeiθ)。
设监测点数量为n,监测点序号为j(j=1~n)。在监测点处,由式(5-19)和式(5-20)求得的映射平面ζ上位移分量uρj,uθj和应力分量σρj,σθj,τρθj必须转换成实际平面z上的位移分量uj,vj和应力分量σxj,σyj,τxyj。映射平面ζ采用极坐标系O-ρθ,而实际平面z采用直角坐标系O-xy,轴x为铅垂向,轴y为水平向左方向。实际平面z上监测点相对应的极坐标的极径ρj已求得,但它的方向需要再根据映射函数求得。监测点处直角坐标与极坐标的关系如图5-3所示,在与监测点j相同极径ρj的轨迹线上取邻近两点j′和j″,它们的极角分别为θj-Δθj和θj+Δθj,Δθj为1°(角θj以铅垂向轴x逆时针向度量),即可求得此两点的坐标差值△xj=xj″-xj′和Δyj=yj″-yj′,亦即得到监测点处极径ρj的方向,θj′=arc tan(Δxj/Δyj)。通常实际平面z上直角坐标系O-xy的轴x为水平向右方向,轴y为铅垂向上方向,注意到把轴x由上述的铅垂向上方向转换为水平向右方向,轴y由上述的水平向左方向转换为铅垂向上方向,因此位移分量(按惯例u为沿轴x向位移,v为沿轴y向位移)和应力分量由极坐标系表达转换为由直角坐标系表达的公式为
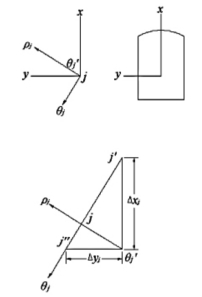
图5-3 监测点处直角坐标与极坐标的关系
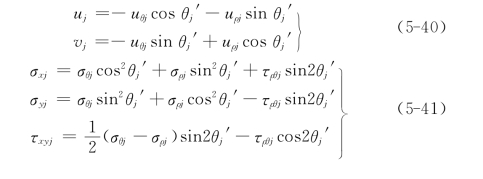
式中:θj为地下洞室纵轴线(铅垂向上方向)逆时针向到监测点的角度。
式(5-40)和式(5-41)是把复变函数方法求得的映射平面上以极坐标表达的位移分量和应力分量转换成实际平面上以直角坐标表达,这对统一建立反分析的观测值方程非常方便。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




