校核与修正钻孔轴向主应力方向的计算结果

研究这个问题时，为使问题简化，围岩的破裂准则，仍采用最大单轴拉应力的破坏准则。水压致裂法地应力测量钻孔岩壁上的应力状态，根据式（3-7）为

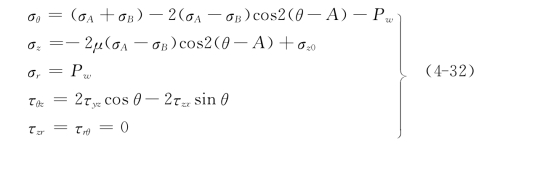
对照式（4-5）可知，水压致裂法地应力测量的经典理论对钻孔轴向就是地应力场中1个主应力方向的假定，实际上就是对岩壁上剪应力τθz为零的假定，这是不合理的。

由式（4-32）可知，钻孔岩壁上剪应力分量τrθ和τzr都为零，故岩壁θz面为一主平面。由于在钻孔岩壁上有剪应力τθz存在，改变了钻孔岩壁上小主应力的量值和方向，也即岩壁上小主应力σM的量值和方向为

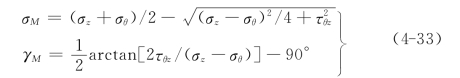
式中：应力分量σθ，σz和τθz用式（4-32）代入，可知σM和γM是应力状态σ和极角θ，液压Pw的隐函数。其中第二式是破裂缝与轴z的夹角（逆时针向度量），是针对产生纵向破裂缝的应力状态σz-σθ＞0而言，而另一状态σz-σθ＜0，则右边要加（或减）90°。

既然水压致裂法地应力测量的破裂缝在钻孔岩壁上最小应力处并在其垂直方向上形成，而最小切向应力，在一般的情况下并不是真正的最小应力，那么就必须研究钻孔岩壁上最小应力的量值和产生的位置，以及产生破裂缝的形式。

根据这一理论，水压致裂法测量时，当液压增加到钻孔岩壁上最小的小主应力σm达到围岩的抗拉强度σt时，钻孔岩壁应该在σm所处的极角θm上产生一组与孔轴相交γm的平行微裂隙。这些微裂隙形成一组雁行缝，并且总体上与钻孔轴向平行。在实际测量中所见到的破裂缝，并不是微倾斜的断断续续的微裂隙雁行缝，而是由它们贯穿起来的一条平行于轴向的纵向缝，这是由于雁行缝产生于较小的极角范围，超过此范围，岩壁上的小主应力不再是最小。它与最小切向应力达到围岩抗拉强度形成的纵向破裂缝不在同一位置上，两者之间相隔一个小角度，它们的破裂缝示意图如图4-9所示［59］。因此，由印模器或钻孔电视记录的破裂缝位置，并不是钻孔岩壁上最小切向应力的位置（也即不是钻孔横截面上大次主应力的极角的位置），而是最小的小主应力的极角的位置。

图4-9　由最小切向应力和最小的小主应力产生的破裂缝示意图

根据以上分析，水压致裂法地应力测量，直接测定而不作任何假设的只有两个参数：一是破裂缝方向θm，另一是破裂面上的法向应力σn（由破裂缝张开时保持与它平衡的瞬时关闭压力PS确定），而钻孔横截面上大、小次主应力σA、σB以及σA的极角A，都需要进行校核与修正。

将式（4-32）代入式（4-33），得到钻孔岩壁上小主应力σM的表达式，利用求极值的条件，得到最小的小主应力σm所处的极角θm，也即得到横截面上大、小次主应力σA、σB以及σA所处的极角A与压裂参数的关系式［60］［61］

(www.xing528.com)

式中：

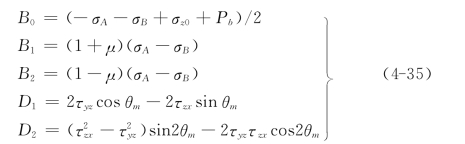
把由式（4-34）求得的A代入式（4-33）第1式，并注意到深层岩体孔隙压力P0的存在，岩体有效应力为σ-P0，即得到最小的小主应力σm的表达式。再根据经典的水压致裂法地应力测量的破裂准则，以σm=-σt代入式（4-33）第1式，得到横截面上大次主应力σA与小次主应力σB和压裂参数的关系式。σA以二次函数求解方式给出

式中：

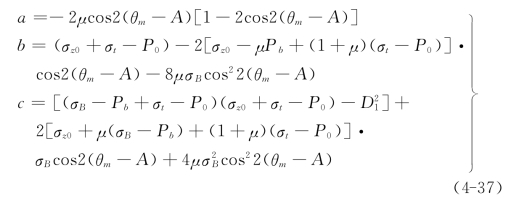
钻孔横截面上小次主应力σB由维持裂缝张开的瞬时关闭压力PS与裂缝面相垂直的法向应力σn相平衡的应力条件σn=PS得到。如图4-10所示，裂缝面上法向应力为

因此得到钻孔横截面上小次主应力

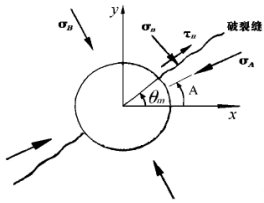
图4-10　钻孔横截面上大、小次主应力与破裂缝位置示意图

这样，钻孔横截面上大次主应力σA，小次主应力σB以及σA所处的极角A，通过联立求解式（4-34）、式（4-36）、式（4-39）3个方程得到。由式（4-34）可见，横截面上大次主应力σA所处的极角A与σA、σB以及压裂参数的关系式以隐函数的形式给出，不能用显式表示，也即A不能直接求得。因此，方程组的求解，在计算技术上采用逐次逼近计算法，σA和σB的初始值为经典理论（假定钻孔轴向为其中的一个主应力方向）计算的值，A的初始值为破裂缝方向的极角。把σA、σB初始值代入式（4-34），并在A的±30°周围搜索，使式（4-34）近似成立。由此求得大次主应力σA的极角A的第一次近似值，再代入式（4-36）和式（4-39）求得大次主应力σA和小次主应力σB的第一次近似值。然后将A，σA和σB的第一次近似值代入式（4-34），式（4-36）和式（4-39），重复以上计算，求得它们的第二次近似值。如此重复计算，直至达到一定的精度为止，最后确定钻孔横截面上大次主应力σA，小次主应力σB以及σA的极角A。