钻孔孔底应变测量法存在的问题及方法

因为钻孔孔底平面应力分量与围岩地应力状态尚无理论解析解，因此，对表达式（3-28）中孔底平面应力集中系数a，b，c，d，只能由模型试验和有限元计算求得。国内外有关单位和学者做了很多工作，但所取得的结果几乎没有一个重复。这就是这种测量方法存在的一个根本性问题。例如范希尔敦（Van Heerden）通过模型试验取得的应力集中系数为a=d=1.25，b=0，c=-0.75（0.65+μ）；克鲁（Cruy，R.V.）通过有限元计算，当μ=0.2时，取得的应力集中系数为：a=1.30，b=0.075，c=0.655，d=1.417；长沙矿冶研究院、兰州大学也通过有限元计算取得的应力集中系数为［45］：a=1.392-0.107μ，b=-0.192+0.393μ，c=-0.4-1.06μ，d=1.584-0.5μ，当μ=0.2时，a=1.370 6，b=-0.113 4，c=-0.612，d=1.484。

由于钻孔孔底平面应力集中系数a，b，c，d的取用值不同，由应变观测值计算得到的应力分量自然不同。

例如，本章第7节工程应用实例中已测定的应力分量（用钻孔坐标系表示）为：σx=3.70MPa，σy=3.64MPa，σz=7.48MPa，τxy=-0.10MPa，τyz=1.01MPa，τzx=-0.66MPa，钻孔孔底应变计端部应变片的布置角φj=0°，45°，90°，120°，3个测量钻孔的布置角相对为β0-βi=0°，45°，-45°。按范希尔顿取得的应力集中系数，计算得到12个应变值（按应变片布置角的顺序）为

ε1j=-0.099 8，-0.294 8，-0.189 8，-0.037 4

ε2j=4.388 2，1.253 4，0.473 2，2.471 6(www.xing528.com)

ε3j=2.065 0，2.062 7，0.130 0，-0.222 1

由这些应变计算值作为观测值，按不同假定的孔底应力集中系数组成各自的12个观测值方程，然后对它们进行解题，求得不同假定的6个应力分量列于表3-20。

表3-20　由不同假定孔底应力集中系数计算的应力分量的比较

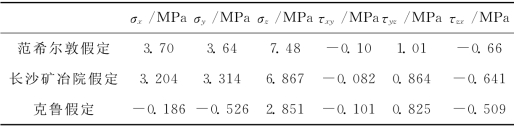
由表3-20可见，由长沙矿冶研究院通过有限元计算确定的应力集中系数计算获得的6个应力分量与原测定的应力分量相差不多，均方差为0.353 4MPa，相对误差为2.8%～18.4%，平均为11.1%；而克鲁通过有限元计算确定的应力集中系数计算获得的6个应力分量与原测定的应力分量相差极大，根本不能相提并论，完全是不同的两回事。由此可知，钻孔孔底应变测量法测量地应力，存在的最大问题是如何准确地确定钻孔孔底平面应力集中系数的问题。