三类套钻孔应力解除测量法的精度评价

3.6.2.1　单个钻孔测量的误差分析

各观测值的误差所导致应力分量误差的大小是不相同的，通常利用均方差来衡量其所导致误差的大小。三类套钻孔应力解除测量法，各个观测值分别有±20×10-6微应变（或相对变形）误差时，由式（3-71）计算，所导致的应力分量误差，列于表3-13。由表3-13可知，导致误差最小的是钻孔孔径变形测量法，平均均方差为0.065MPa；钻孔孔壁应变测量法的误差稍大一些，平均均方差为0.078MPa，为钻孔孔径变形测量法的1.20倍；而钻孔孔底应变测量法的误差为最大，平均均方差为0.169MPa，是其他两类测量方法平均均方差的2.2～2.6倍。

由岩石弹性常数取用值的误差所导致的应力分量误差对三类测量方法都相同，所导致的应力分量误差相对于地应力量值的百分数，就是弹性模量取用值误差相对于弹性模量取用值的百分数。

表3-13　三类测量方法，当应变（或相对变形）观测值有20×10-6误差时所导致的应力分量误差

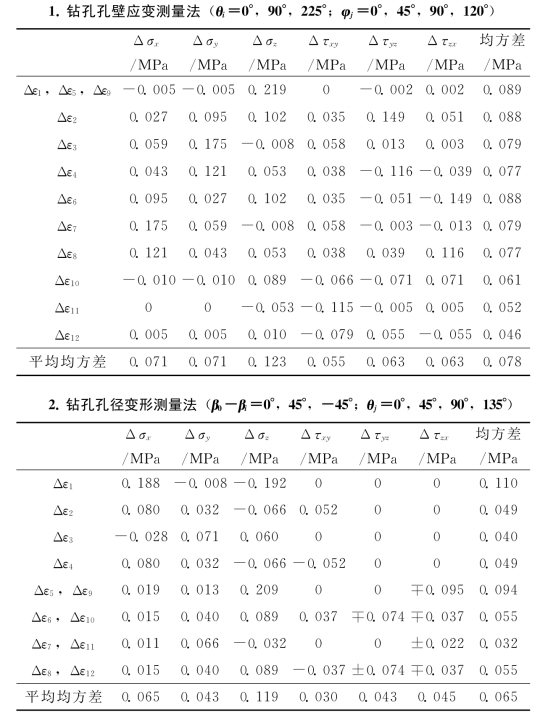
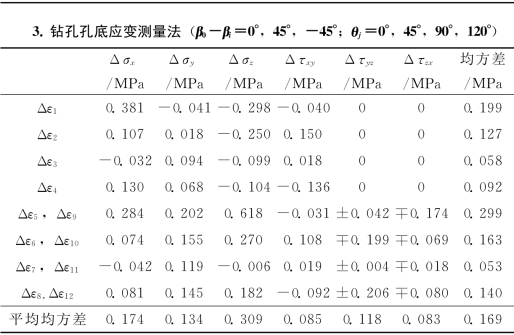
注：E=40GPa，μ=0.20。

3.6.2.2　三孔交汇测量的误差分析

1）两斜钻孔角度有偏差时所导致的误差

钻孔孔径变形测量法和钻孔孔底应变测量法，都需要在3个交汇钻孔中分别进行测量才能测定三维地应力状态。但在三孔交汇测量中，两斜钻孔的角度往往不易控制，容易发生偏差。同样，也以三峡工程Ⅲ-7.53m测点所测定的地应力状态为例（设它们与垂直岩壁钻孔的夹角有±5°偏差时）进行具体分析，所导致的误差计算结果列于表3-14。由表3-14可见，1个斜钻孔有偏差时所导致应力分量误差是比较大的；若两个斜钻孔以相对或相反方向偏差时，则导致的误差更大，其中以顺垂直岩壁钻孔的轴向应力分量的误差Δσz为最大。表3-14还说明钻孔孔底应变测量法所导致的误差比钻孔孔径变形测量法所导致的误差约大1.7倍。钻孔孔径变形测量法和钻孔孔底应变测量法所导致的总误差相当于钻孔孔壁应变测量法的观测值有±90.53～96.53微应变误差时所导致的总误差。(www.xing528.com)

表3-14　两斜钻孔角度有±5°偏差时所导致的应力分量误差

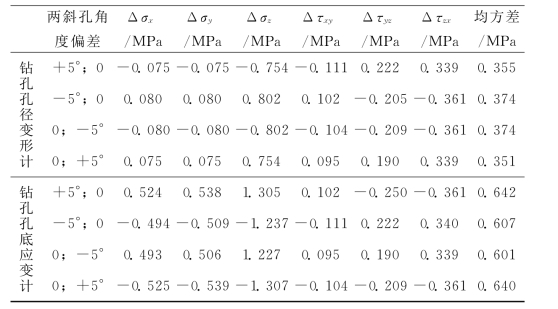
注：计算应力分量误差条件同表3-12，钻孔布置同表3-13。

2）两斜钻孔（分）测点弹模有变化时所导致的误差

众所周知，交汇测量的3个钻孔不可能交汇到一点。例如垂直岩壁钻孔深10m，两斜钻孔与它夹角为45°，当它们有±5°偏差时，则两斜钻孔（分）测点就偏离垂直岩壁钻孔0.9m，这样，就可能因地质条件的不同引起弹性常数的差异。设垂直岩壁钻孔10m处弹性模量为40GPa，两斜钻孔（分）测点弹性模量有±5GPa变化时（相对垂直岩壁钻孔（分）测点弹性模量的1／8），以实例计算，其所导致的应力分量误差列于表3-15。由表3-15可知，两斜钻孔（分）测点的弹性模量同时变大（或变小）产生应力分量的误差比以相反形式变化的情况要大得多；但是，钻孔孔径变形测量法和钻孔孔底应变测量法的总偏差却非常接近。两斜钻孔（分）测点的弹性模量同向变化和反向变化的总偏差，相当于钻孔孔壁应变测量法观测值有±129和±97左右微应变误差时的总偏差。

表3-15　两斜钻孔（分）测点的弹模有±5GPa变化时所导致的应力分量误差

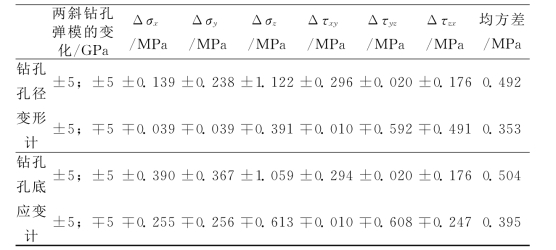
注：已知应力分量同表3-12；E=40GPa，μ=0.2；钻孔布置同表3-13。

3.6.2.3　对三类测量方法精度的评定

如上所述，从单钻孔测量比较，钻孔孔径变形测量法的误差最小，钻孔孔壁应变测量法的误差稍大一些，钻孔孔底应变测量法的误差最大（见表3-13）。但是由于三孔交汇测量时，斜钻孔的角度偏差和（分）测点弹性模量差异所导致的误差较大。表3-14和表3-15还说明，当斜钻孔有±5°的偏差和弹性模量有1／8差异（在实际中远远大于此值）时，钻孔孔径变形测量法产生的总偏差，相当于钻孔孔壁应变测量法的观测值有±188～226微应变误差的总偏差，这就使钻孔孔径变形测量法的精度大大降低。此外，钻孔孔底应变测量法不论在单钻孔测量还是三孔交汇测量，它的精度都是最低的。所以，测量精度最高的是钻孔孔壁应变测量法，其次是钻孔孔径变形测量法，最差的是钻孔孔底应变测量法。