套钻孔应力解除测量法系统误差分析

3.6.1.1　由应变观测值不准确所导致的误差

设某一应变观测值的误差为Δεi，由此导致应力分量实测值的误差分别记为Δσx，Δσy，…，Δτzx，于是用最小二乘法原理求解，必须满足方程

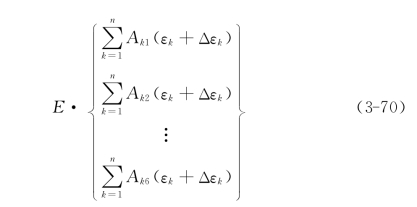
式（3-70）减去式（3-41），得到

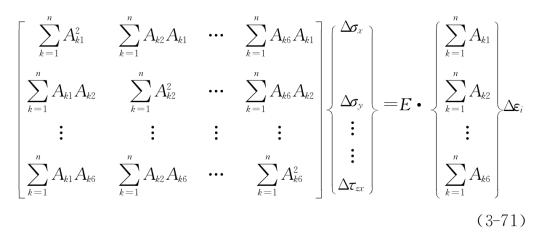
由式（3-71）可知：①由观测值误差导致的应力分量误差，仅仅与观测值误差大小有关，与观测值本身大小无关，也即与地应力状态无关；②因为所导致的应力分量误差同地应力状态无关，因此导致的误差就不能用地应力量值的百分数来表示；③观测值误差与其所导致的应力分量误差是正比的线性关系。

今以CJS-1型钻孔三向应变计为例，12个应变观测值误差，在弹性常数E=40GPa和μ=0.2情况下，导致的各个应力分量的误差如图3-29所示。由图3-29可知，正应力分量σx（或σy）的误差，主要由与其方向垂直的应变丛的3个应变观测值（除轴向应变观测值外）的误差所致，其次由与其方向平行的应变丛的3个应变观测值（除轴向应变观测值外）的误差所致；正应力分量σz的误差，主要由与其方向一致的3个轴向应变观测值的误差所致；剪应力分量τxy的误差，主要由与轴x和轴y交45°角的应变丛的3个应变观测值（除轴向应变观测值外）的误差所引起；剪应力分量τyz（或τzx）的误差，主要由与轴x（或轴y）一致的应变丛中斜交的2个应变观测值的误差所引起的。

图3-29　CJS-1型钻孔三向应变计由应变观测值误差所导致应力分量的误差

（a）Δε1～Δεx（Δεy） （b）Δε1～Δσ2（c）Δε1～Δτxy（d）Δε4～Δτyz（Δτzx）

3.6.1.2　由弹性常数取用值不当所导致的误差

套钻孔应力解除测量法是采用间接测量法测定地应力状态，也即是通过对岩体应变的量测来确定地应力。因此，岩石弹性常数必须参与计算，其取用值的准确度直接影响推算的地应力状态的精确性。

设弹性模量取用值误差为ΔE，由此导致应力分量误差，类似式（3-71）推导可导出(www.xing528.com)

与式（3-41）联立，可得到所导致的应力分量误差Δσ与相对应的应力分量σ之比

由式（3-73）可知：①弹性模量的取用值误差与其所导致的应力分量误差是成正比的线性关系；②所导致的应力分量误差相对于地应力的百分数，也就是弹性模量取用值误差相对于弹性模量取用值的百分数；③因为弹性模量取用值误差对各应力分量具有相同百分数的影响，所以对岩体主应力只影响其大小，不影响其方向。

例如弹性模量取用值为40GPa，弹性模量取用值误差为5GPa，那么，导致的应力分量误差Δσ=σ·5／40。

泊松比取用值误差所导致应力分量误差的关系比较复杂，不能用显式表示，但导致应力分量的误差并不大。例如以CJS-1型钻孔三向应变计实测的三峡工程Ⅲ-7.53m测点为例，各应力分量随泊桑比变化的曲线如图3-30所示。由图3-30可知泊桑比取用值的误差对σx和σz的影响较大。当泊桑比取用值为μ=0.2，其取用值误差为Δμ=±0.05时，对应力分量产生的误差平均约Δσ=±0.14MPa，最大也不超过（Δσ）max=±0.62MPa。从图中也可看到泊松比取用值误差所导致应力分量的误差软岩比硬岩大。

图3-30　三峡工程Ⅲ-7.53m测点泊桑比对应力分量的影响

3.6.1.3　应变丛和应变片位置的偏差所导致的误差

在实际操作中，应变丛和应变片的粘贴，不可能完全做到精确无误，与设计角度有一些误差。因此，它们的位置发生偏差，必然会导致应力分量误差。所导致的误差也比较复杂。对这个问题的研究也通过实例计算。例如，以三峡工程Ⅲ-7.53m测点所测定的地应力状态为例，当CJS-1型钻孔三向应变计θ=90°应变丛和φ=90°应变片布置角度有±5°偏差时，所导致的应力分量误差列于表3-12。由表3-12可知，应变丛布置角度的偏差所导致的应力分量误差是比较大的，尤其对与其垂直的应力分量σx的误差为相对σx量值的13.43%（θ=90°时，有+5°和-5°误差导致的应力分量误差的平均值）。由应变片布置角度的偏差也导致一定程度的应力分量误差。

表3-12　θ=90°应变丛和φ=90°应变片布置角度有±5°偏差所导致的应力分量误差

注：计算应力分量误差条件：Ⅲ-7.53m测点所测定的应力分量：σx=9.193，σy=2.420，σz=1.128，τxy=4.740，τyz=0.162，τzx=1.407（单位：MPa），E=40GPa，μ=0.2。