主应力的强度及方向判定方法

根据正规方程组（3-41）求得三维应力状态的6个应力分量σx，σy，…，τzx以后，大、中、小主应力σ1，σ2，σ3的量值以及它们的方向（包括它们的倾角αi和方位角βi）也可求出。

3个主应力σ1，σ2和σ3的量值由三维应力状态的特征方程

求得。式中J1，J2和J3为应力张量的第一、第二和第三不变量：

式（3-55）为一元三次代数方程，作变换σi=S+J1／3，则方程（3-55）变为

其中：

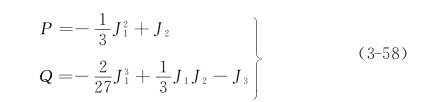
再作一次变换得

这是的二次代数方程，它的解为

因此，代数方程（3-55）的判别式为。

当时，方程式（3-55）有3个实根，其中两个实根互等，主应力为

当时，方程式（3-55）有3个不相等的实根，

主应力为

(https://www.xing528.com)

其中：

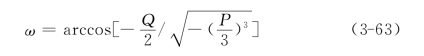
当时，方程式（3-55）有1个实根和1对共轭复根，这种情况对岩体主应力计算没有实际意义。

主应力方向由静力平衡方程

中的任两式和方向余弦的关系式

联立解得。

取方程组式（3-64）中前二式，并改写为

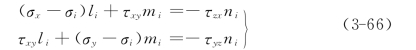
由此，方向余弦li，mi可以用ni表示，再代入式（3-65），得到方向余弦，并注意到取ni＞0，则方向余弦li，mi和ni为

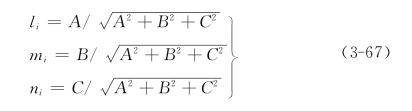
其中：

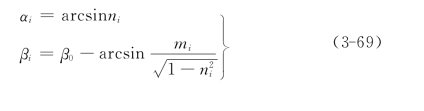
为了和地质上的概念相互联系起来，主应力方向以倾角和方位角来表达。倾角为主应力矢量与水平面的夹角，方位角为主应力矢量在水平面上的投影与正北方向的夹角，顺时针向为正。考虑到大地坐标系轴x一般与正北向不一致，设轴x的方位角为β0，如图3-7所示，因此主应力的倾角αi和方位角βi根据几何关系为

图3-7　主应力的倾角和方位角