应力分量最佳值的确定方法

地应力测量既为多值测量，即观测值方程的数目多于6个应力分量未知数，这就需要采用数理统计的最小二乘法原理，求解它们的最佳值。

四种不同形式的套钻孔应力解除测量法的观测值方程组（3-11）、（3-19）、（3-24）和（3-32）都以统一格式给出，它们的区别归纳于不同的应力系数Ak1～Ak6的表达式上。观测值方程组中εk（对钻孔孔径变形测量法为Uk／d）和σx，σy，…τzx都为真值的物理量，但由于现场条件和测试技术的影响，真值物理量是测不到的。因此观测值方程组可表示为

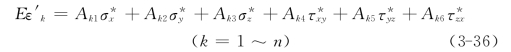
式中：n为观测值个数，ε′k和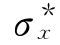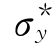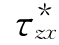，，…为观测值和由此推算得到的岩体应力分量的最佳值，以区别于实际存在的应变（或变形）的真值和应力分量的真值。

一组观测值ε′k与其真值εk的偶然误差Xk（Xk=ε′k-εk）发生的概率为［30］

式中称为精度（m为总体的均方差）。若ε′k为一组等精度观测值，则偶然误差Xk同时出现的概率为

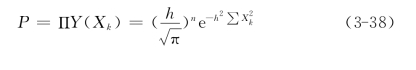
由于观测值的最佳值（最可信赖值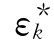）最接近真值εk，它出现的概率为最大，当P最大时，=最小。但是一个物理量的真值是无法测得的，更不可能衡量其偶然误差，今用观测值的残差代替Xk，于是由上式得

这就是数理统计最小二乘法原理，即在一组等精度观测值来确定最佳值，就是求各观测值的残差平方和为最小。

由此，建立误差方程组

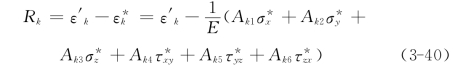
为书写方便，今后都不再带上角标“′”和“＊”。

利用最小二乘法原理，满足式（3-39）的条件为

(www.xing528.com)

于是得到求解应力分量最佳值σx，σy，…τzx的正规方程组

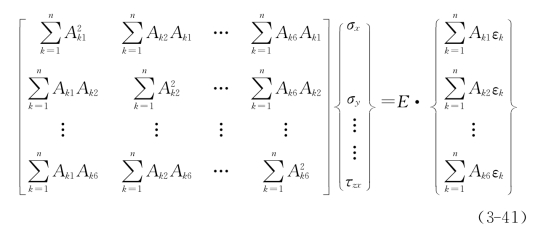
求解方程组（3-41）得到的应力分量最佳值，代入式（3-40）求得观测值残差Rk。于是观测值的标准误差为

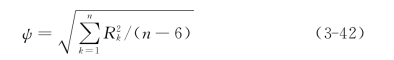
而应力分量最佳值σx，σy，…τzx的标准误差为

式中：i为相应于应力分量σx，σy，…τzx的注符，Qii为应力分量的权倒数，按待定系数方法求得：

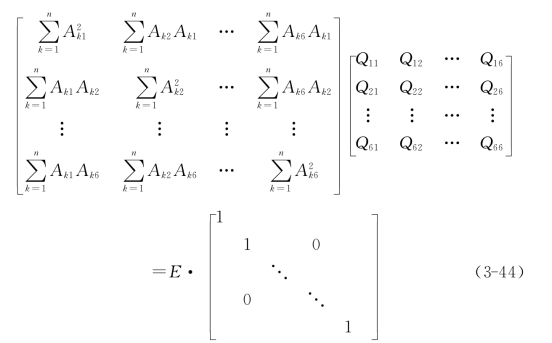
但是，用少量的观测值来估计总体的真值是会有一定误差的。要正确估计其可靠程度，必须确定真值存在的范围，并给出可信度。对于按正态分布的总体，可用学生氏T分布来估算抽样误差及其最佳的置信度［31］。因此，岩体应力分量最佳值σx，σy，…，τzx的误差为

若取95%的置信度，则T（n-6））如表3-2。

表3-2　取95%置信度时学生氏T分布值

对现场实测得到的观测值数据，必须经过科学的分析整理。首先由全部应变观测值进行统计计算，按正规方程组（3-41）求解应力分量的最佳值以后，进行误差分析，从中舍弃其中残差最大的一个观测值，再对剩余的观测值进行统计计算，如此反复筛选，直至剩下最后6个观测值为止。具体计算过程参阅工程应用实例计算表3-23。

每一测点地应力状态的确定，应当是在对第一现场实测资料和计算机计算结果作了全面分析的基础上得出的。也就是说，既要分析整个现场测量过程中出现的现象和测点周围的地质构造情况，以及测量中应变观测值随解除深度变化的规律；还要研究计算机计算中对观测值和应力分量取舍的合理性，以及误差分析的情况。从而得到正确的判断和合理选取。