地应力场变化规律分析

1.3.2.1　自重应力场的变化规律

由于地心对岩体的引力，使地壳岩体始终处于自重应力场之中。岩体自重应力可以通过计算获得。计算的理论是建立在岩体是均匀连续的弹性介质假定基础之上的。

假定岩体简化为均质半无限弹性体，忽略地质构造和地形变化对地应力的影响。自重应力场随深度的变化如图1-4所示，在地表以下埋深H的研究点，岩体的铅垂应力σ′z为：

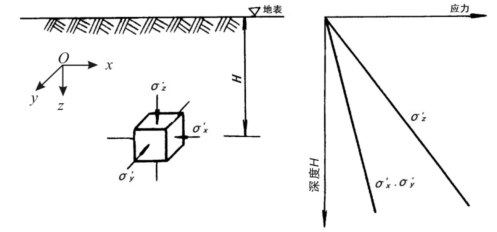
图1-4　自重应力场的变化规律

当埋深较小，且上覆岩层为多层不同岩体时，σ′z为

式中：γi为上覆各层岩体重度；Hi为上覆各层岩体厚度。岩体的水平应力为：

在半无限体情况下，单元体上的正应力分量σ′z，σ′x，σ′y也就是主应力σ1，σ2，σ3。侧压系数λ可以根据半无限体侧向变形为零的条件求得，沿任一水平方向，例如x方向引起的应变等于零，得到

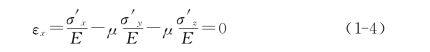
式中：E，μ分别为岩体的弹性模量和泊松比。

又因为σ′x=σ′y，所以求得

上式与式（1-3）比较，则得侧压系数λ为

岩石的泊松比μ通常在0.10～0.35之间，对坚硬岩石其值较小，对松软岩石其值较大。因此在自重应力场中λ值在0.11～0.54之间，而主要在0.25～0.43之间（即μ=0.2～0.3）。

当μ=0.5时，得到λ=1，所以海姆假说是金尼克假说的一个特例。但这一观点还未得到实践的证实。有人认为，在塑性岩体中以及极大深度地层，海姆假说比较接近实际。

1.3.2.2　地质构造应力场的变化规律

研究地质构造运动的成因以及它的驱动力是非常复杂而颇有争议的问题。很多学者提出了自己的理论，其中以板块运动（大陆漂移）学说已经得到地学界的支持。因此，地质构造应力一般认为主要是水平向作用力［9］。

假定地质构造应力S为沿水平轴x方向的作用即坐标轴x，y，z都与应力场的主方向一致，它随深度的变化如图1-5所示。则在地表附近和浅层岩体引起的应力场为

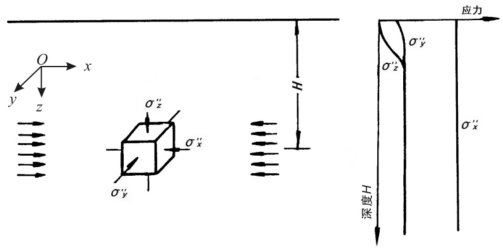
图1-5　地质构造应力场的变化规律(www.xing528.com)

在深部岩体引起的应力场为

若在受构造应力S作用之前，已有与S成β角的构造应力S′存在（角β以S′方向为起始逆时针方向度量），则通过坐标转换公式，将构造应力S′形成的应力分量转换到坐标系O-xy表达，然后再与构造应力S形成的应力分量叠加，即可求得深部岩体在水平面上的应力分量为

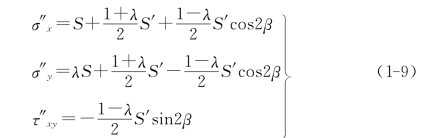
再将坐标绕轴z旋转到主平面方向，也即构造应力S和S′合成以后主应力的量值类似式（1-8）为

式中：轴x′和轴y′是合成后的构造应力场的主方向。大主应力σx′的方向角β0（与轴x的夹角，逆时针方向度量）为

1.3.2.3　地应力场的变化规律

取自重应力场的主轴与地质构造应力场的主轴一致，采用代数叠加，就可求得以自重应力场和地质构造应力场（假定仅受一次地质构造运动）为主要组成成分的地应力场，它随深度的变化如图1-6所示。在地表附近和浅层岩体的地应力场为

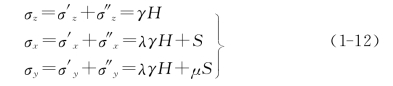
在深部岩体的地应力场为

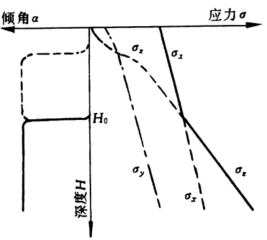
图1-6　地应力场变化规律

——大主应力　---中主应力　—-—小主应力

图1-6给出了地应力场沿深度的变化规律，从而对地应力场的变化可得到以下几点认识：

（1）地应力场的各应力分量，除靠近地表以外，沿深度的变化均可用线性方程来概化，即沿深度呈直线变化。

（2）地应力场中的主应力量值沿深度呈折线变化。大主应力σ1在浅层为水平向主应力σx，到达一定深度以后才转变为铅垂向主应力σz；中主应力σ2在浅层为铅垂向主应力σz，到达一定深度以后转变为较大水平向主应力σx。它们是由两个直线段所组成，其转折点深度H0称为临界深度，可令σx=σz求得。注意到式（1-1）、式（1-3）和式（1-10）经简单运算以后就可得到临界深度H0。当只经受一次地质构造运动时，临界深度为

对经受二次地质构造运动时，临界深度为

（3）地应力场随深度而变化，在临界深度H0以上是以地质构造应力场为主导，大主应力为水平方向为主，其量值随深度增加的幅度较小；在临界深度H0以下，就转变为以自重应力场为主导，即大主应力为铅垂方向，其量值随深度增加的幅度较大，大致以岩体容重的增率增加。至于临界深度附近，存在一个地质构造应力场为主导逐渐转变为以自重应力场为主导以及主应力量值和方向逐渐调整变化的过渡带。