结构光法测量原理简介

结构光法属于光学投影式三维轮廓测量方法，根据三维数据计算方法的不同，又可以分为直接三角法和相位法。直接三角法是以纯粹的三角测量原理为基础，由投影点、物体表面点和像点三者之间的几何成像关系确定物体各点高度。相位法是由条纹的形变量得到相位变化，再由相位和高度的映射关系来获得相对于参考面的三维数据，其优点在于分辨率高，数据获取速度快。相位法也利用了三角法原理，但其技术核心是相位信息的解调。

将结构光图像投射到被测物表面，从另一个角度可以观察到由于受物体高度的调制而变形的条纹，这种变形可解释为相位和振幅均被调制的载波信号。采集变形条纹并对其进行解调，恢复出相位信息，进而由相位确定出高度，这就是基于相位的结构光方法的原理。图5.32为典型的交叉光轴系统结构光法测量原理。

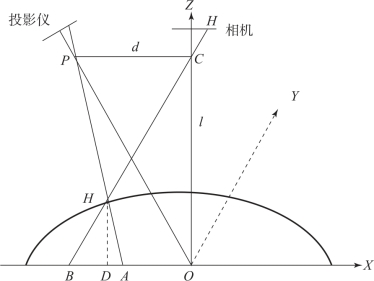
图5.32　结构光测量原理图

图中，OP 是投影系统透镜的光轴，它与成像透镜的光轴OC 交于点O。OX 所在的平面为参考平面（可以是虚拟的，也可以是真实存在的），OC 垂直参考面。P 和C 分别为投影透镜出瞳中心和成像透镜的入瞳中心，两点的连线与参考面平行，距离为d，离参考平面的距离为l。正交坐标系的XOY 平面位于参考平面上，Y 轴垂直于XOZ 平面并与X 轴交于O点，Z 轴平行于成像透镜光轴。投射光栅交于物体表面点H，H 成像在像面上H′点。PH 与参考面交于点A，CH 与参考面交于点B，A、B 两点之间的距离表示为s（x，y）。物体表面点H 相对于参考面的高度为h（x，y），由△PHC 与△AHB 相似可以得到

假设投影的是正弦光栅，规定系统的相位零点正好在坐标系OXYZ 的原点，则参考面和物体表面上各点的光强可以分别表示为I0（x，y）和I（x，y），即

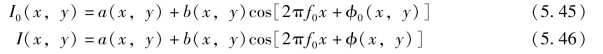
式中，a（x，y）和b（x，y）分别表示背景光强和物体表面反射率的变化；f0=1/p 为投影到参考面上光栅条纹的空间频率。相位Φ0（x，y）和Φ（x，y）分别对应于在参考面和被测物体表面的相位分布。物体表面相位分布与参考面相位分布的相位差表示为ΔΦ（x，y），可以证明A、B 两点之间的距离s（x，y）和相位差ΔΦ（x，y）满足如下关系：

将式（5.47）代入式（5.44），即可以得到(www.xing528.com)

这样只要得到物体表面每点相对参考面的相位差ΔΦ（x，y），就可以计算得到高度值，实现三维轮廓测量。

图5.33为计算机仿真产生的正弦光栅投影在参考面和球体表面的条纹图，从图5.33（b）可以看出受被测球体高度的调制作用，正弦光栅条纹产生了形变。

图5.33　条纹投影在参考面和球体表面

（a）参考面条纹图；（b）球体表面条纹图

利用相位提取方法可以得到参考面和被测物体表面的相位分布，从而计算得到相位差。图5.34为由图5.33所示的条纹图得到的相位分布，其中图5.34（a）为参考面上的相位分布，图5.34（b）表示球体表面相位，图5.34（c）为包裹相位，图5.34（d）是采用相位展开方法进行解包裹后得到的真实相位。只要得到了真实的相位分布，根据式（5.48）和系统标定的结果就可以得到被测球体的三维数据。

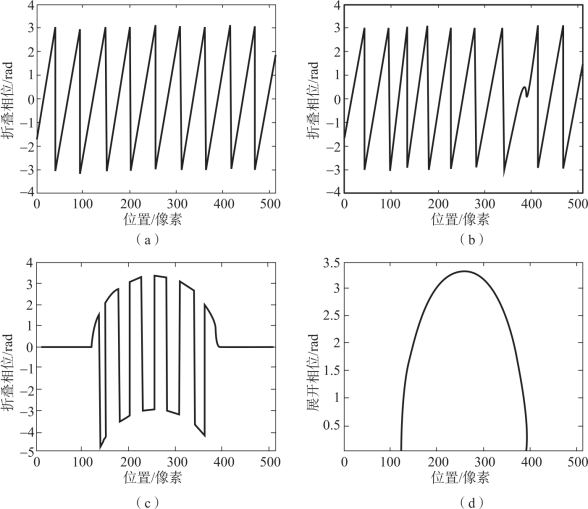
图5.34　相位分布

（a）参考面相位；（b）球体表面相位；（c）包裹相位；（d）解包裹相位