莫尔测偏法：简介与应用示例

5.3.2.1　简介

莫尔测偏法也是一种非接触式光学检测法。该法产生于1980年，其基本原理是根据被测物体所引起的莫尔条纹偏移量来测量被测物的特性。该法适用于镜面反射物体，如光学非球面等，因此常与干涉法进行比较。与干涉仪相比，莫尔测偏法装置简单，对振动不敏感，造价低廉，适于现场检测。此外，莫尔测偏法具有可调整的灵敏度，可针对不同的用途调整为不同的测量精度，同时，测量范围较大，可达几毫米，这是一般干涉仪所不能比拟的。应该指出的是，该法的精确度较之干涉法相对较低，这是它的原理所致。但由于它具有上述众多的特点，尤其是抗干扰能力强，因此有望用于非球面零件的现场在线检测。

5.3.2.2　测量原理

简单的莫尔测偏仪如图5.11所示，它由光源和两块朗奇光栅（Ronchi Grating）构成。两块光栅G1、G2 以一定的间距d 平行放置，它们的栅线相对于X 轴各形成θ/2 和-θ/2 的倾角。在光源的照射下，第一块光栅的阴影投射到第二块光栅上，形成平行于Y 轴的莫尔条纹（图5.12），条纹的间距为

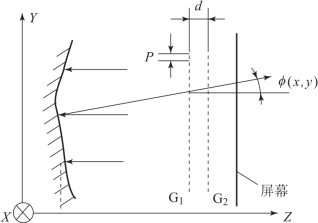
图5.11　莫尔测偏仪原理

图5.12　莫尔条纹形成原理

式中，P 为栅距。

当有被测表面存在于光栅后面时，照射光线受被测表面反射会引起莫尔条纹偏离其未受扰动的位置。其偏移量δh（x，y）反映了被测表面特性。光线偏移角φ（x，y）与偏移量δh（x，y）之间有如下关系：(www.xing528.com)

式中，θ≪1。由此可见，根据条纹偏移量δh（x，y）以及栅线偏角θ 和光栅之间距离d 则可计算偏移角φ（x，y）。而光线偏移角φ（x，y）从本质上而言表示了被测面某点（x，y）处的梯度，有如下公式：

式中，H（x，y）表示物体在点（x，y）处的表面高度。

由此可见，在求取x、y 两方向上的偏移角φ（x，y）之后，进行曲线积分，便可求得某点的高度。而求取φ（x，y）的关键，则是从莫尔偏移图上求得莫尔条纹的偏移量δh（x，y）。图5.13是一幅莫尔偏移图。为得到偏移量δh（x，y），通常采用如强度法、自动条纹检测法、外差读取法等，直接计算得到像素或亚像素偏移量。上述方法受限于条纹宽度和探测器分辨率，一般来说精度较低。

图5.13　有限宽条纹莫尔偏移图

引进移相技术是对传统的莫尔测偏法的一大改进。我们已经知道，在干涉条纹测量系统中广泛使用着相位计算技术，这种方法的优点是具有很高的精度，由于它能精确计算整幅干涉图各点的相位，因此其评价精度比条纹数字化技术高出

数十倍到上百倍。另外，它能整幅处理被测图像，具有很高的速度。从本质上讲，莫尔条纹可写成光强的形式：

式中，Ψ（x，y）为莫尔偏移图上各点的相位，是与光线偏移角φ（x，y）直接相关的一个量，α（x，y）为由于光栅X 方向上的位移引起的附加相位角。为求得Ψ（x，y）可将一块光栅移相3 次，相当于α（x，y）变化3 次。则可得3 个方程，由此便可解得Ψ（x，y）。由Ψ（x，y）则可求得φ（x，y），最终可求得被测表面高度。