使用转动法测量曲率半径较小表面的表面形貌

转动法的测量原理如图5.6所示。与平移法不同，转动法测量过程中，检测台不移动，被测面绕其最佳参考圆的圆心C 转动。最佳参考圆的圆心C 和半径R，是以被测面在转动过程中，激光反射光束的最大偏转角度为最小而定，用以减小测量误差。转台带动被测面以一定的角度间隔Δθ 转动，就可测得被测面上间隔Δθ 的各点处的斜率，通过计算得到被测表面的形貌。

图5.6　转动法测量原理图

设S 为光斑位置相对于零点的距离，a 为激光入射方向上被测点与分束镜的距离，b 为入射激光和分束镜的交点与CCD 光敏面的距离，2β 为激光反射后的偏转角，则与平移法相同，被测点处的斜率为

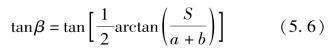
然后就可以根据被测面上各点的斜率，利用式（5.7）计算出被测面的表面形貌：(www.xing528.com)

式中，ρ（θ）为被测面上角度为θ 处的点与最佳参考圆圆心的距离。

与平移法类似，在实际测量中a 是未知的，可以测得的是在激光入射方向上最佳参考圆与分束镜的距离a0，并且a（θi）=a0+R-ρ（θi），a（θi）为θi 处激光入射方向上被测点与分束镜的距离。

所以在计算被测点的高度时，先用a（θi-1）代替式（5.6）中的a，并由式（5.7）计算出ρ1（θi），再将这个ρ1（θi）代入到a（θi）= a0+ R- ρ（θi）中，得出一个a1（θi），再用a1（θi）代替式（5.6）中的a 重新计算tanβ，并再次由式（5.7）计算出一个ρ2（θi）。如此反复迭代计算，逐渐逼近ρ（θi）的真值，直至先后两次计算得出的ρk（θi）与ρk+1（θi）之差小于某个值，则将ρk+1（θi）作为计算出的ρ（θi）值。

这种方法适用于测量曲率半径较小的表面。