基于迭代变换的PDPR算法优化

1998年美国加州大学喷气推进实验室（JPL）的研究人员在探索“下一代空间望远镜”（Next Generation Space Telescope，NGST，后更名为James Webb Space Telescope，JWST）的相关波前传感技术中，提出了一种“稳健”的PDPR 算法——MGS（Modified G-S）算法。之后，研究人员为了使MGS 算法能够具有更大的波前传感动态范围，将多种相位解包裹技术引入算法中，提出了波前传感精度高且动态范围较大的Baseline 算法。

1.MGS 算法

如图4.21所示，MGS 算法除了使用焦面光强数据外，还引入两个离焦面（其离焦位置关于焦面对称）的光强数据，基于式（4.91）并行建立3 组G-S 迭代，每一次循环中各组均使用相同的迭代相位初值，并在完成一次G-S 迭代之后进行加权平均，从而获得下一次循环的迭代相位初值，重复以上步骤直至各组G-S 迭代的焦面（离焦面）光强均收敛至测量值，各组G-S 迭代的瞳面相位趋于一致。

图4.21　MGS 算法流程图

MGS 算法的实质是在不增加变量维数的前提下，通过获得关于待求变量更多的信息，求得唯一、准确收敛的解分布。它的提出标志着迭代变换算法逐步走向成熟应用阶段。

虽然MGS 算法可获得较高的传感精度，但是它未能解决当波前分布PV（峰谷）值大于一个波长时相位分布中出现的2π 不定性问题，这使得该算法的波前传感动态范围受限于一个波长。此外，焦面的光强分布过于集中，以此作为一组G-S 迭代很难获得收敛理想的迭代结果。

2.Baseline 算法

在MGS 算法中，各面的迭代相位估计被包裹在（-π，π] 之中，因此一旦被测波前分布的PV 值大于一个波长，各面的估计就不能直接加权求和，需要通过解包裹获得真实相位估计后才可加权求和。为此，JPL 的研究人员提出Baseline 算法，对MGS 算法做了多处改进，其中最关键的是提出了包括路径无关型相位解包裹算法和无权值最小二乘相位解包裹算法在内的混合解包裹算法。

Baseline 算法框图如图4.22所示。算法包括多个针对不同离焦面采用G-S 算法的内循环和一个外循环，它首先对各个内循环的迭代包裹相位估计，使用混合解包裹算法完成相位解包裹，之后对各解包裹相位分布作加权平均，并把平均相位分布作为下次内循环的初始相位。此外，由于各离焦面引入的离焦“相位变更”不同，在进行G-S 迭代之前和之后需要添加和剔除各面的“相位变更”量φDiversity（d）。同时，光学系统自身的像差也被考虑在内。

综上所述，Baseline 算法不但继承了MGS 算法使用“相位变更”的思路，从而具有解的唯一性和较优的传感精度，又解决了相位包裹对MGS 算法传感波前动态范围的限制，被视为解决相位恢复问题的首选迭代变换算法。但Baseline 算法迭代前期的收敛速度和方向并不十分理想，且不适用于具有大动态范围、光瞳内存在区域遮挡的波前传感。

3.PDPR 模型中的目标函数

使用前S 阶Zernike 多项式，光瞳相位分布φ（x0，y0）可描述为

式中，u 为阶数；Zu（x0，y0）为第u 阶Zernike 多项式的表达式；αu 为第u 阶多项式的系数。

将式（4.93）代入式（4.91），使用FFT 实现傅里叶变换并取模的平方，可获得离焦面fD 上的光强分布IModel（x，y，fD，α），为

(www.xing528.com)

式中，P 代表P（x0，y0）；φ 代表φ（x0，y0，α）；φDiversity代表φDiversity（x0，y0，d）；α 为前S阶Zernike 系数构成的向量；上标∗表示取复共轭。

同时，由探测器测得离焦面fD 上的光强分布为ISensor（x，y，fD），对两光强分布各自进行归一化得和，可建立离散形式下参数最优化算法的目标函数F：

式中，M×N 为离散矩阵的大小。

4.基于梯度计算的参数最优化算法

在最优化理论中，使用目标函数梯度信息计算搜索增量的算法有许多，其中适合相位恢复模型的主要有3 种：最速下降法，共轭梯度法和牛顿法。其中，牛顿法还使用了目标函数的二阶偏导信息，基于它的简化算法有L-M 算法和阻尼高斯-牛顿法。

1982年，Fienup 提出用最速下降法或共轭梯度法求解相位恢复问题，并对各算法的迭代性能作了比较。到20世纪90年代初期，为检测哈勃望远镜的成像系统失调像差，Fienup沿用早前提出的这两种算法，取得了较好的结果。另外，Redding 提出用L-M 算法求解该相位恢复问题，并也取得与之一致的测量结果。

直到今天，最速下降法、共轭梯度法和L-M 算法仍然是最常用的3 种参数最优化算法，并分别适用于不同参数表达形式下的目标函数。其中，对于使用Zernike 多项式描述波前的目标函数，由于各阶模式相对于目标函数的贡献很不一致，使得用前两种方法准确求解各阶模式系数的难度很大，使用L-M 算法较为合适。

L-M 算法是牛顿法的简化算法，它不直接计算目标函数F（α）关于αu 的二阶偏导矩阵（Hessian 矩阵）中的S（α（k））项，而是用一个可调节系数和一个单位矩阵共同构造一个正定对角矩阵来替换它，通过调节系数值使算法在迭代初期具有最速下降方向，在迭代后期具有高斯-牛顿（Guass-Newton）收敛方向。

L-M 的迭代公式为

式中，α（k）为第k 次迭代解向量；d（k）为α（k）的迭代增量；l（k）为第k 次迭代的可调节系数；I为S 阶单位矩阵；H（α（k））是由（m，n）面内各点的h（m，n，fD，α（k））值构成的列向量，长度（维数）为M×N，其中，

J（α（k））为h（m，n，fD，α（k））关于αu 的Jacobi 矩阵。

因此，设定最佳的l（k）值，是L-M 算法收敛的关键。h（m，n，fD，α（k））关于αu 的一阶偏导为

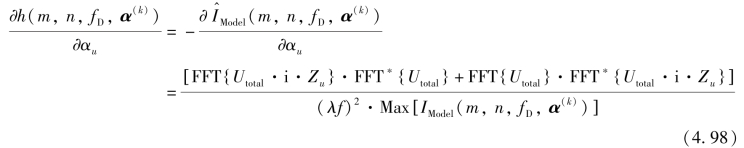
式中，Max [IModel（m，n，fD，α（k））]为IModel（m，n，fD，α（k））分布中的极大值；Zu 代表Zu（x0，y0）；Utotal=P·exp（i·φ）·exp（i·φDiversity）。

由式（4.97），可完成对L-M 迭代公式（4.96）的计算。