相位变更与恢复的模型优化

在相位恢复波前传感中，显然必须确保解的唯一性，但这恰恰是G-S 算法无法保证的。在随后的20年里，研究人员深入探讨了G-S 算法的收敛性以及光瞳相位解的唯一性等问题，并提出了多种修正的G- S 算法。直到1993年，Roddier 将离焦型“相位变更”（phase diversity）引入相位恢复模型中，相位恢复算法才找到了实质性的突破方向。

所谓“相位变更”，其思路是在瞳面上附加已知的相位分布（“相位变更”），从而获得附加前后的多幅焦面光强分布，继而根据数量倍增的已知条件，排除仅满足任何单一条件的解，找到同时满足所有条件的解，从而提高解的唯一性。若瞳面、焦面各采样N 个点，则由式（4.88）可建立N 个方程。但因这两个面上的相位均未知，故有N+N=2N 个未知量，导致解不唯一。通过相位变更，可获得另N 个方程，用这2N 个方程去求解2N 个未知量，原则上便可获得唯一解。

Roddier 提出的离焦“相位变更”引入方法是：通过探测焦面附近已知距离的离焦面光强分布，等效于探测在光瞳面引入离焦“相位变更”后的焦面光强分布，由此获得一系列不同离焦“相位变更”下的焦面光强分布。不同于其他类型的“相位变更”，离焦“相位变更”的实现简单、无须标定，并且能有效扩大探测面光斑（离焦面点扩散函数）尺寸，从而降低对探测器信噪比的要求，增加更多的光强分布信息。

1.（0，fD）相位变更相位恢复模型

对式（4.85）中（d1，d2）取（0，fD），其中fD=f+d，d 为离焦距离，方向沿光传播方向。于是，εd1d2=f+d，式（4.85）变为

其中，式（4.90）右端积分式外的相位因子不体现在光强中。于是，在fD 处探测离焦面PSF 即等效于在光瞳面引入离焦“相位变更”φDiversity（x0，y0，d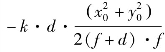）=后在焦面探测PSF。对比式（4.87）和式（4.90），发现两傅里叶变换的唯一差别在于与空间域（x0，y0）对应的空间频域离散采样由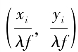变为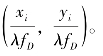

因此，在（0，fD）相位变更相位恢复模型中，对于确定的空间域（x0，y0），不同fD（不同离焦面）对应的空间频域采样间隔应该不同；换言之，需要对探测器在不同离焦面拍摄的光强分布数据进行重采样，以调整各个面上的采样间距。(www.xing528.com)

重采样将带来额外计算量和插值误差是显见的，于是Fienup 运用角谱传播理论提出改进的（0，fD）相位变更相位恢复模型，使各离焦面的采样间距一致。首先，依式（4.90）获得d=d1 处的离焦面复振幅分布U（x，y，fD1）；随后，对U（x，y，fD1）进行空间频率分解获得各平面波分量的角谱，并依角谱公式计算光场从d=d1 处传播到d=d2 处的角谱；最后，由各平面波分量的角谱组合出fD2处的离焦面复振幅分布U（x，y，fD2）。在该模型中计算不同离焦面的光强分布，都需要从fD1焦面开始。

2.（f，fD）相位变更相位恢复模型

对式（4.86）中（d1，d2）取（f，fD），其中fD=f+d，d 的含义同于（0，fD）模型中的叙述。于是，εd1d2=f，式（4.86）变为

同样，在fD 处探测离焦面PSF 即等效于在光瞳面引入离焦“相位变更”φDiversity（x0，y0，d）=- k·d·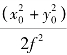后探测焦面PSF，并且不同离焦面上的空间频域采样间隔均保持一致。

（f，fD）相位变更相位恢复模型较之（0，fD）模型更为适用于实际波前传感要求。下文中相位变更相位恢复（Phase Diversity Phase Retrieval，PDPR）模型，若不做特殊说明，均指（f，fD）相位变更相位恢复模型。