相位恢复的基本模型

对于由点光源发出的光波在光学系统瞳面上的波前相位分布，相位恢复算法的思路是基于光瞳面和光瞳频谱面之间的傅里叶变换关系，已知光瞳频谱面的光强分布，求解光瞳面的相位分布。

通常，使用透镜可以实现对光瞳面的频谱变换。首先，我们给出透镜的一般变换公式。如图4.18所示，正透镜焦距为f，物面位于透镜前d1 处，观察面位于透镜后d2 处。设物平面的光场分布为U0（x0，y0），透镜前、后表面的光场分布为U1（x′，y′）和U2（x′，y′），观察平面上的光场分布为U（x，y）。

图4.18　透镜的变换效应

假设光场在d1和d2距离上的传播满足菲涅耳近似条件，通过对光场U0（x0，y0）完成一次菲涅耳积分（遵循自由空间光传播理论）可以获得透镜前表面的光场U1（x′，y′），之后引入透镜的相位变换因子

式中，j2=-1；k 为波矢数。(www.xing528.com)

可以获得透镜后表面的光场U2（x′，y′），再对光场U2（x′，y′）完成一次菲涅耳积分，可以获得观察平面上的光场分布

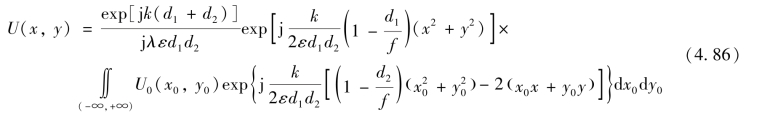
式中，λ 为光波波长；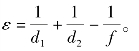

当（d1，d2）取（0，f）或（f，f）时，式（4.86）右端的复杂积分式均可简化为傅里叶变换式，分别为

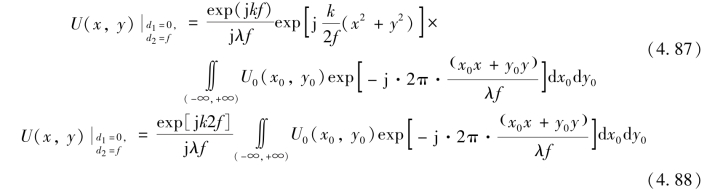
于是，依（0，f）或（f，f）设置瞳面和观察面相对于透镜的位置关系，则观察面即为光瞳频谱面。这就是相位恢复算法中常用的两种数学模型，简称为（0，f）型和（f，f）型。注意到两种模型的光瞳频谱面均取透镜的后焦面，将“光瞳面与光瞳频谱面”直接称为“瞳面-焦面”。

这样，相位恢复问题归结为：已知傅里叶变换对的各自振幅分布，求解相位分布。对于这个求逆问题，英国剑桥大学的两位学者Gerchberg 和Saxton 于1972年提出了经典的迭代傅里叶变换算法，后称为G-S 算法。