使用模式法重构波前相位

1.波前相位展开

区域法估计波前相位是利用子孔径四邻位置的测量数据估计中心点相位的方法。模式法与此不同，它将全孔径内的波前相位展开成不同的模式（例如平移、倾斜、离焦、象散、彗差和球差等），然后用全孔径内的测量数据去求解各模式的系数，得到完整波前展开式，从而重构出波前。

一个复杂的二维波前分布需要用一组正交多项式的线性组合来简化描述，例如，一个完整的波前φ（x，y）可以用多项式展开成F（x，y）：

式中，nk 为归一化常数；ak 为待定系数。

为了方便，使Fk（x，y）的平均值为零，即

相位方差为

式中，a0 为相位的平均值。

多项式Fk（x，y）是正交多项式，即

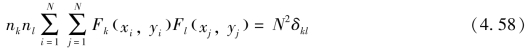
式中，δkl为克罗内克符号。

可供使用的正交多项式种类有很多，光学中最常用的多项式是Zernike 正交多项式，其各阶表达式能很好地与波前像差理论对应。尤其当被描述的波前分布以低阶像差模式为主时，仅仅一组数目有限（多项式的前几十阶）的Zernike 多项式系数就能准确地拟合出被描述的波前分布。

目前，Zernike 多项式常用两套不同的描述形式，分别由Malacara 和Noll 完善，如表4.2所列（仅列前21 阶）。这两套表达式的区别如下：关于极坐标（ρ，θ）的定义不同，参见表中的第2、3 阶表达式；关于各阶多项式相互正交的定义，这两套多项式有不同意义的归一化系数，使得Noll 提出的这套多项式各阶多出一个常系数（角向数m 不为0时）或（角向数m 为0 时），其中为n 径向数；此外，在同一径向数下，这两套多项式的排序也不同。因此，使用Zernike 多项式描述波前分布时，一定要指明采用了哪套定义式，以免重构波前时发生错误。

表4.2　两套Zernike 多项式的表达式对比（前21 阶）

实际工程中，在分析大气扰动的畸变波前分布时，多采用Noll 多项式描述波前分布；在其他的光学测量领域（面形、波像差测量）中，多采用Malacara 多项式描述波前分布。选用Zernike 多项式，波前可展开为

上式是波前相位展开式的连续形式。实际上有用的是离散形式，即

为求解展开系数ak，需要用到波前斜率展开式，从中求得系数ak，再根据波前相位展开式恢复波前相位。

对式（4.60）微分，即得

式中，εx 和εy 为测量误差。因为波前传感器只能测量子孔径（i，j）内的平均斜率，则

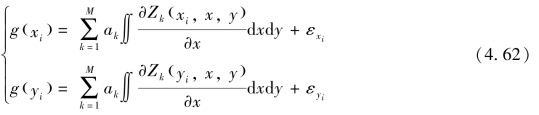
用矩阵符号表示为

式中，Φ 为N×1 维矢量；Dφ 为N×M 矩阵；A 为M×1 维矢量；G 为2N×1 维矢量；Dg 为2N×M 矩阵；Ag 为M×1 维矢量。为了方便，令A=Ag。

因为实际上所取的模的阶数不多，即M≪2N，所以模式法需要的数据量要比区域法的数据量少得多，按模式法构造的自适应光学系统也比按区域法构造的自适应光学系统简单，不过后者具有更高的响应速度。

2.最小二乘解

与区域法求解式类似，方程组可以求最小二乘最小范数解

(www.xing528.com)

由于Zernike 多项式大部分低阶导数的正交性，所以系数A 可以独立地通过对斜率的加权和而得以确定。由此导致的结果是，DTD 是对角线矩阵。对角线矩阵的逆仍然是对角线的，其对角线元素是对应元素的倒数，所以不再需要数值程序。

因为Zernike 多项式的部分低阶不正交，则DTD 不再是对角线的，不过，因为这种情况为数不多，所以DTD 仍是对角线为主的稀疏矩阵，求逆DTD 也能很快完成。

3.格兰-史密特正交解

由于直接求DTD 的计算误差可能会导致矩阵奇异，同时变为法方程系数矩阵De 后，解的条件数会大大增加，故引入格兰-史密特方法。先给定正交函数q，用q 展开波前相位φ，再通过最小二乘法求得展开式系数B，最后根据B 与Zernike 多项式展开系数A 之间的关系，求得系数A。

设正交函数qi （ρ）对全部数据都是正交的，即

式中，δμr是克罗内克符号。用qi （ρ）展开波前相位，有

使

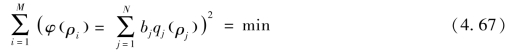
可得到最小二乘解

式中，Q 为2M×N 阶矩阵，列间正交，则

将矩阵Dg 分解为Dg=QR，其中R 为N×N 阶上三角矩阵，于是

有了新函数系bj 和三角矩阵R，再用矩阵求逆法，即可求得Zernike 函数的系数Ag。因为R 是三角的，R-1易于求解，故

还可以采用简单迭代法，求解三角方程，从中求得Zernike 系数Ag。

4.奇异值分解法

使用一系列选主元的Householder 变换和带原点移位的QR 方法对矩阵A 施行奇异值分解

式中，U（M×R 阶）和V（N×R 阶）为次酉矩阵（R 个标准正交列矢量并排构成的矩阵），U 和V 分别为矩阵的左、右奇异值矢量；S（R×R 阶）为含有A 矩阵奇异值的对角矩阵。

并有

于是，描述方程的最小二乘最小范数解的广义逆有如下形式：

奇异值分解是一种数值稳定性相当好的算法，不管矩阵条件数如何，用奇异值分解得到的广义逆求解方程，在最小二乘最小范数下都能得到稳定解。

5.直接积分解

假设波前离散化的采样点是均匀分布的，则可以从Zernike 多项式的正交关系直接求得展开式系数a，即

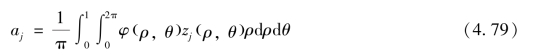
这是展开系数aj 的真正定义值。至于由式（4.64）和式（4.73）求得的都是aj 近似值。为了提高后者的精度，要求采用高阶多项式。这样做会导致奇异方程，因而无法求解。鉴于一般的波前展开用低阶项近似的精度已经足够，同时计算较为简单，故得到广泛应用。式（4.79）的二维积分是很复杂的，有理论意义却并不实用。