自基准哈特曼检测方案探究

通常测量仪器都会基于一个全局坐标系进行测量。被测物体被置于全局坐标系中，测量时仪器不断获得物体上的采样点在这个全局坐标系中的坐标，最后通过这些采样点的坐标重构出物体的形状。但有些测量系统没有全局坐标系，而是利用已经测出的曲线形状进行仪器自身的定位，并以此确定的位置为基准进行下一点的测量，得出采样点相对于这个基准的位置，然后再以新测出的曲线部分加上已知的曲线部分来确定仪器的方位，不断进行上述循环，直至测出全部曲线的形状，称为自基准测量。

自基准测量在难以建立高精度大型基准或空间工作等场合有重要应用，如：以地面目标为被测对象的卫星相机在轨工作时，由于受失重和温度变形等因素的影响，常常引起光学零件变形和光学系统失调，影响成像质量。采用主动光学技术进行校正，需要准确探测相机的波像差。如采用上节介绍的夏克-哈特曼波前传感器进行波前误差测量，需要提供一个无限远的点光源作为信标。选用自然星作为信标，需经常改变卫星的飞行姿态，增加卫星的能耗，且检测状态与使用状态不完全一致会影响校正效果。选用激光导星信标，所需脉冲激光的功耗很大，也不适用于太空条件下的工作的卫星系统。此时，如何解决波前传感器的信标问题，便成为卫星相机能否成功应用主动光学技术的关键问题。

基于波前径向斜率测量原理的新型哈特曼波前传感器是一种无须任何外部信标而利用机内自身信标的方法，其原理如图4.14所示。点光源发出的光波经被测光学系统后，形成有波前畸变的平面波。五棱镜P1可单独沿被测物镜光瞳的半径方向平移，也可与五棱镜P2一起绕被测物镜的光轴转动。P1和P2的主截面彼此平行，并与光轴方向一致。当P1沿径向平移时可实现对被测物镜出射光束的离散采样。采样光束通过P1和P2后，被会聚成像在CCD相机靶面上。

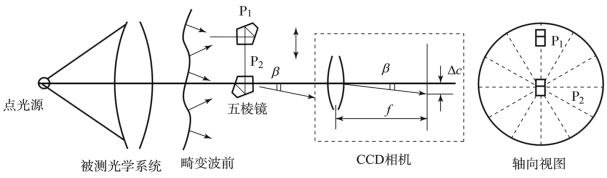
图4.14　自基准哈特曼波前传感器的光路原理图

测出P1处于光瞳面内不同位置（ρ，θ）时所对应的像斑质心坐标和相对偏移量的径向分量，由式（4.24）即可求得被测物镜出射波前斜率的径向分量：

对于以离散波像差形式表示的原始测量数据，通常用Zernike 多项式作最小二乘拟合求出被测波前的形状，这已为大家所熟知和广泛采用。对于以离散径向斜率值形式表示的原始测量数据，改用Zernike 多项式的径向斜率形式作最小二乘拟合，同样可以求出被测波前的形状。(www.xing528.com)

理论分析和计算机仿真结果表明，在采样密度足够的情况下，根据已知波前径向斜率分量的离散采样值也完全可以以足够高的精度重构出原始波面的形状。如果径向斜率离散采样值包含有一定的随机误差，也仍能重构出精度与波前径向斜率采样精度相当的波前形状。用Zernike 径向斜率多项式作最小二乘拟合具体过程如下。对波面上每一点的径向斜率测量数据可分别写出

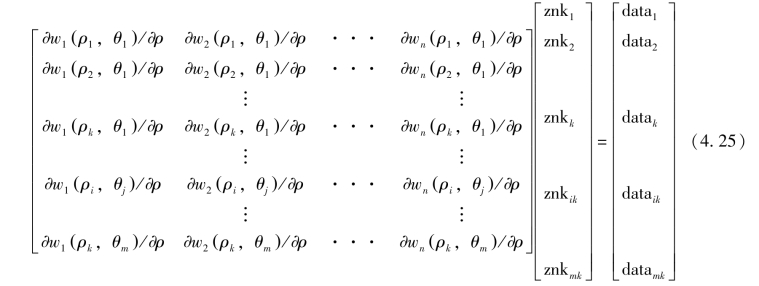
式中，∂wn（ρi，θj）/∂ρ为单位圆上（i，j）点处第n 项Zernike 多项式的径向斜率值，也就是以Zernike 多项式形式表示的基元波面的斜率值；znk1…znkk 为第1～n 项Zernike 多项式的系数；data1…datamk为被测波面上各采样点处的径向斜率测量值；k 和m 分别为半径方向和圆周方向的采样点数。上式也可以用简单的矩阵形式表示为

由于测量点数k×m 总是大于Zernike 多项式的项数n，所以由上式可写出最小二乘解为

基于波前径向斜率测量原理的新型哈特曼波前传感器，无须另外提供检测基准就可以对光学系统像质进行检测，省去大口径标准面或大口径平行光管，也无须用自然星作点目标。扫描机构快速无冲击，简单、稳定、可靠，波前测量灵敏度与干涉仪相当，而对工作环境和光源并无苛刻要求。此技术不仅可用于卫星相机主动光学系统的高精度波前传感，而且可用于地基天文望远镜和其他大口径光学成像系统的像质检测。