探究夏克-哈特曼测量原理

夏克-哈特曼测量原理由帕特拉和夏克于1971年提出，该方法放弃使用带有子孔径阵列的光阑，代之以使用微透镜阵列状的光阑。这种方法与传统的哈特曼检验法相比有很细微但又非常重要的区别。

（1）传统哈特曼检验方法中，哈特曼图案是由一束靠近焦点的会聚光得到的，在夏克-哈特曼传感器中则是在一束近乎准直的光束中进行检验。

（2）夏克-哈特曼检验法能够轻易检验并测量出正负离焦，而传统哈特曼法则不行。

（3）夏克-哈特曼检验中，子光斑聚焦在探测器上，光能量密度比传统哈特曼检验中的光能量密度高出若干数量级，更适用于弱光探测。

其测量原理如图4.13所示，入射波面到达微透镜阵列后被子透镜划分为子孔径阵列，进入每个子孔径的细光束经微透镜聚焦到探测器靶面上，形成光斑阵列。入射波面是理想波前，即平面波时，CCD 得到的光斑阵列刚好位于微透镜阵列光轴与CCD 芯片的交点附近位置处，如图4.13（a）中的虚线位置所示；若入射波面含有波前畸变，则焦面CCD 上得到的光斑位置将偏离理想位置，形成不规则的光斑阵列，如图4.13（a）中的实际光束与CCD芯片的交点位置。这些散乱光斑与理想位置的偏离量包含了波面的畸变信息，每一个子孔径内的平均波前斜率正比于光斑偏移理想位置的距离。计算这些散乱光斑的二维质心位置偏离理想位置的距离，除以焦距，便可得到各子孔径的波前二维斜率，运用波前重构算法即可重构出入射波前相位分布。

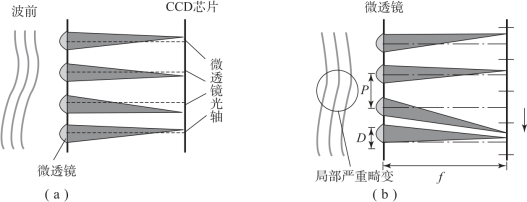
图4.13　夏克-哈特曼测量原理

（a）局部波前斜率误差较小；（b）局部波前斜率误差较大

微透镜口径较大时，波前采样分辨率低，由子孔径平均斜率重构波前的精度受限；微透镜口径较小时，波前采样分辨率提高，但每个子孔径对应的探测器区域变小，即斜率误差测量范围变小。当波前局部斜率误差较大时，某些子透镜形成的光斑会落入周边子孔径对应的探测器区内，如图4.13（b）所示，造成斜率测量出错。

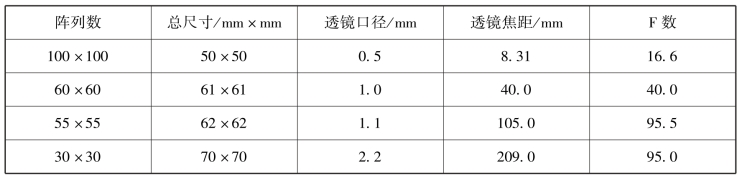
夏克-哈特曼检验的透镜状光阑最初由两层完全相同且相互垂直的柱状透镜构成，现在可以使用塑料、玻璃等制作微透镜阵列。常见的夏克-哈特曼阵列是一个10 ×10～100 ×100 的微透镜阵列，每块透镜的直径大约在0.2～2 mm。近年来，甚至有超过1 000 ×1 000微透镜产品出现。微透镜典型焦距F 数在F10～F200。表4.1给出了常见的夏克-哈特曼传感器中微透镜阵列的主要参数。(www.xing528.com)

表4.1　典型夏克-哈特曼传感器中微透镜阵列的主要参数

透镜衍射光斑的半径ρ 由式（4.21）表示：

式中，d 和f 分别为透镜的直径和焦距；λ 为光波的波长。

夏克-哈特曼传感器的测量范围定义为在确保光斑不交叉或重叠的情况下能够测得的最大局部波前偏角。因为光斑偏离量的最大允许值是d/2-ρ，所以角度动态范围为

探测器的像素大小σ 决定了传感器的角度灵敏度，该灵敏度定义为对最小可测得角斜率求导数，可由式（4.23）表示：

系数k 与光斑位置计算方法有关，采用质心等计算方法时，光斑定位精度通常可达到亚像元水平，即k 可以小于1。由于探测器上的光斑位移等于波前斜率乘上小透镜的焦距，焦距越短波前斜率测量动态范围就越大，但灵敏度也随之降低。