相位解包裹方法简介

在式（4.13）中，相位是通过反正切函数求得的，目前几乎所有的移相算法都是以反正切的形式给出的。反正切函数的值域在（-π/2，π/2] 区间内，根据正、余弦等的正负可将值域扩大到（-π，π]，超出该区间的原始相位值会被加减2π 的整数倍压缩到该区间内。我们把通过反正切运算得的、丢失了相位整数级次信息的，限制在（-π，π] 的相位称作包裹相位，如图4.2所示。

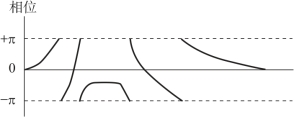
图4.2　包裹相位

设待测面是光滑的，相位也应该是连续的。实际干涉条纹中大多含有多条明暗条纹，意味着相位变化超过2π。当真实相位超过2π 时，运用反正切求解相位会有2kπ 的整数相位丢失，造成相位跃变。为了消除包裹相位的跃变，需要对包裹相位数据进行处理，使计算得到的波面连续，称为相位解包裹，图4.3表示解包裹后的相位。

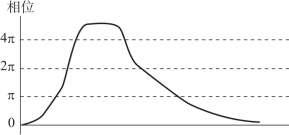
图4.3　解包裹后的相位

解包裹的方法分为路径法与全局法两大类，其中路径法较为清晰易懂。一个包裹的相位图可以看作由一个平滑的相位图被压包在（-π，π] 之内得来。理想干涉图中含有多条条纹时，每条条纹的相位变化在-π～π，总的相位变化大于2π。选某一基准点为0 相位，将平滑相位图中大于π 的相位减去2kπ，小于- π 的相位加上2kπ，使所有的相位分布在（-π，π] 区间内，即形成包裹相位图，其中k 为整数。同一级次干涉条纹的k 相同，不同级次k 不同，相邻级次k 相差1。(www.xing528.com)

由以上分析不难发现如下规律：

（1）k 和干涉条纹级次一一对应，可以直接作为条纹级次使用；

（2）处于同一级条纹的相位被压包在一个连续区域，不同级条纹的相位被压包在不同区域，相邻级次条纹交界处存在-π→π 或π→-π 的跃变；

（3）同一级条纹的相位被压缩在-π～π 之间，加上2kπ 即可恢复相位，k 为该条纹的级次。包裹相位φ 和解包裹相位ψ 之间满足

式中，k 为整数。相位解包裹问题即转换成求解干涉条纹级次k 的问题。相邻级次条纹交界处的相位存在跃变，跃变反映在二维图中就是一个明显的边界。边界线将整个包裹相位图划分成若干个区域，每个区域对应一个干涉条纹级次k。