移相干涉技术的工作原理解析

图4.1所示为移相干涉的原理图。图中泰曼-格林干涉仪置于空气中，参考镜由压电晶体带动，可沿光轴方向进行精细（纳米量级）的平移运动。

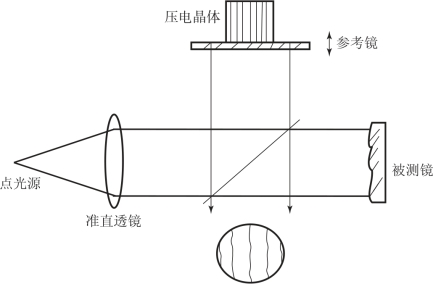
图4.1　移相干涉光路原理图

设某时刻，参考镜相对于初始位置沿光轴方向向上移动li，则参考波前为

被测镜的面形误差分布为W（x，y），则被测波前为

式中，a 为参考波前的振幅；b 为被测波前的振幅；参考光波和被测光波基础光程相等，均为L/2；W（x，y）为被测镜的面形误差分布，当被测镜垂直于光轴时，反射引入的被测波前光程变化量为W（x，y）的2 倍。

参考波前与被测波前经分光镜合束后发生干涉，干涉条纹的光强分布为

式（4.3）表明，对被测波面上所有的点，I（x，y，li）是li 的余弦函数，因此可以写出它的傅里叶级数形式为

式中，a0 为傅里叶级数的直流项；a1 和b1 分别为傅里叶级数基波分量的系数。将式（4.3）进行三角函数展开为

比较式（4.4）和式（4.5）可得

由式（4.6）可以看出，被测面的面形是由傅里叶系数的比值求得(www.xing528.com)

由于式（4.7）中存在a1、b1、W（x，y）三个未知量，要从方程中解出W（x，y）至少需要移相3 次采集3 幅干涉图。

对每一点（x，y）的傅里叶级数的系数，还可以用三角函数的正交性求得

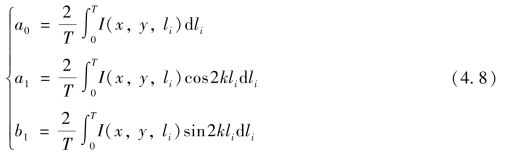
为了便于实际的抽样检测，用和式代替积分，有

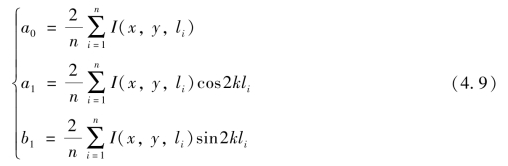
式中，n 为参考镜振动一个周期中的抽样点数。于是，式（4.7）变为

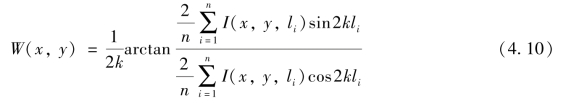
特殊地，取四步移相，即n=4，使，则

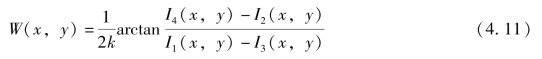
由于式（4.11）中含有减法和除法，干涉场中的固定噪声和面阵探测器的不一致性影响可以自动消除。这是移相干涉技术的一大优点。

相应地，若取n=5 时，被称作五步移相。在实际应用中，三步移相、四步移相、五步移相都被广泛应用，三步移相需要的干涉图数量最少，最方便快捷。但随着相移步数的增加，位相差的求解精度也相应地会提高。

为了提高测量的可靠性，消除湍流、振动及漂移的影响，可以测量傅里叶级数的系数在p 个周期中的累积数据：

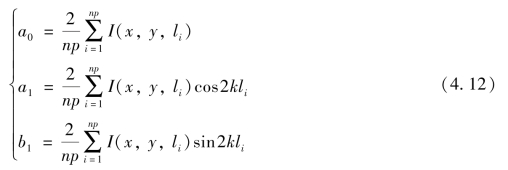
从最小二乘法意义上来看，式（4.10）所表达的傅里叶级数是被测镜轮廓的最佳拟合。再由式（4.7）可得

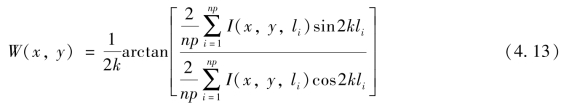
因此，在被测镜面上任意一点（x，y）的波面相位是由在该点的条纹轮廓函数的n ×p个测定值计算得到的。部分求和的形式要求数据无限地积累，通过最小二乘法拟合，使相位误差或波面误差减少至原来的。对被测面上的每一点（x，y），由每次所累加的数据（a0，a1，b1），可按式（4.13）求出W（x，y），画出被测镜的面形误差分布图。