光频梳绝对距离测量技术优化

1.光频梳基本原理

2005年，美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）的Hall 教授与德国马克斯·普朗克光学研究所的Hansch 教授，因以下研究工作而分享了当年的诺贝尔物理学奖：对飞秒激光器载波包络相移频率及重复频率的锁定，研制光学频率梳，光频梳在光学频率测量方面的成功应用。从原理上看，光频梳是将各纵模频率锁定至频率基准的锁模激光器，其光谱由一系列分立的纵模组成，重复频率即为激光器的纵模间隔，L 为谐振腔的长度，c 为真空中光速。如图3.34所示，任一纵模的频率为fm=mfr+f0（f0 称为偏置频率），由谐振腔内色散和相位调制作用决定。fr 和f0 可以直接锁定至微波频率基准，通过正整数m 的桥接作用，光频fm 也实现了与微波频率基准的锁定。

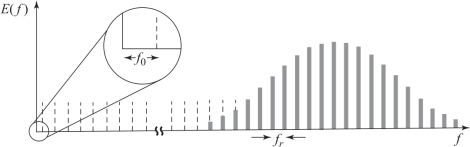
图3.34　光频梳光谱

由图3.34可知，在频域上光频梳的电场可以表示为

式中，A（f-fc）为光谱包络函数，fc 为光谱中心频率。

单纵模线宽远小于总的光谱宽度，因此使用δ 函数对其进行模拟。将式（3.61）中频率转变为角频率，并对其进行傅里叶变换，可以得到光频梳光场的时域表达式

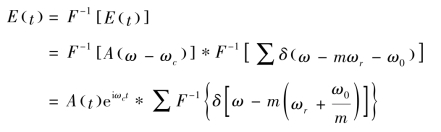
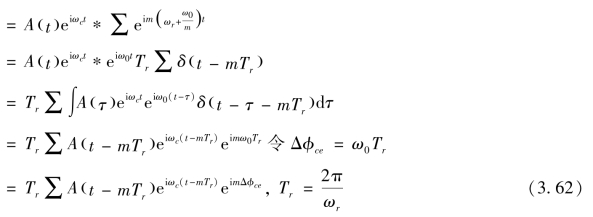
式中，A 为脉冲包络；Tr 为重复周期；ωc 为光谱中心频率对应的角频率；Δφce为载波包络相移，表示包络峰值与载波峰值的相位差。

由式（3.62）可以看出，光频梳电场的时域形式为周期性脉冲序列，重复周期为Tr，图3.35示出了其时域电场。

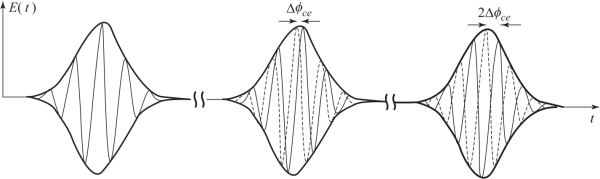
图3.35　光频梳时域电场

因此，光频梳在时域上为一系列等时间间距的脉冲，在频域上为一系列等频率间距且相位锁定的纵模，并且其各个纵模都可以溯源到频率基准。长度基准基于光在真空中的传输速度，而时间基准基于原子钟的频率，因此光频梳将两个基本物理量的基准结合在了一起，可以作为非常高精度的频率基准，从而可以在精密计量领域发挥重大作用。人们也利用光频梳频域上精准的频率特性以及时域上周期脉冲特性，研究出一系列绝对距离测量的方法。此类技术的优势体现在两方面：①光频梳实现了时间基准和长度基准的连接，从而可以实现绝对距离测量结果直接溯源到米的定义；②光频梳具有的宽广谱、窄脉冲特性为实现新型激光绝对距离测量提供了更多可行的方向。

2.光频梳绝对测距技术

根据测量原理的不同，可将光频梳测距的方法分为5 类：光频梳频标合成波长法、模间拍频合成波长法、脉冲对准时间飞行法、色散干涉法以及双光梳法。

1）光频梳频标合成波长法

这种方法不使用光频梳直接测量，而是将其作为一个频率标准，利用其精确的频率特性为传统合成波长法中的可调谐激光器提供频率参考。如图3.36所示，将可调谐激光器通过拍频鉴相的方式锁定至光频梳，作为测量光源。可调谐激光器频率为fcw=mfr+f0+fb，其中m 的数值可以通过光波长计来确定，通过将fr、f0 及fb 锁定至微波频率基准，实现对可调谐激光器频率的精确锁定。锁定之后，通过调谐fr 产生合成波长，然后根据频率（波长）扫描干涉的方法进行绝对距离测量。

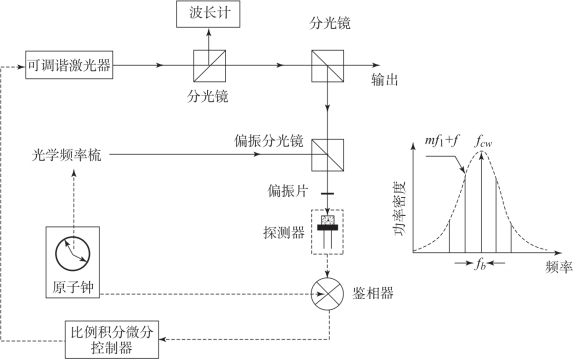
图3.36　光频梳频标合成波长法测距系统原理图

使用光频梳作为频率标准的合成波长法进行绝对距离测量精度可以达到8 nm，并且测量结果可以溯源到频率基准，在测量精度以及溯源性上相对于传统的方法都有提升。但是扫描时需进行多波长分时测量，测量时间长，要求被测目标的位置基本不变，并且合成波长链的建立依赖于初始值的测量。因此，这种方法不适用于初值未知的大尺寸绝对距离测量；此外，由于要分时串行测量，其测量速度也受到一定限制。

2）模间拍频合成波长法

光频梳本身具有多个纵模，并且各纵模之间有着稳定的相位关系，因此可以直接通过这些纵模来产生合成波长链进行绝对距离的测量。相对于以光频梳作为频标的系统，此方案中光源得到简化，并且无须频率扫描，能够实现短时测量，适合实现对运动目标的绝对距离测量。如图3.37所示，光频梳重复频率为fr，因此纵模之间的拍频值为fr，2fr，…，n fr，在射频上表现为一系列间隔为fr 的频率分量。这些拍频频率及相位稳定，因此可以利用不同的拍频组合形成波长链来进行绝对距离的测量。

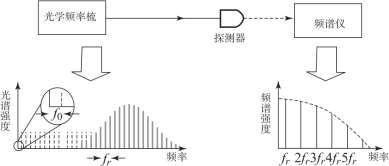
图3.37　纵模间拍频合成波长原理

此方法于2000年由日本科学家Minoshima 提出，并且在240 m 的距离上实现了标准差50 μm 的绝对距离测量。但是由于使用的拍频频率低，拍波波长长，对于确定的相位细分能力，仅依靠纵模间拍频形成的合成波长链测量精度有限。为进一步提高测量精度，使用声光移频外差干涉的方式，将合成波长的最后一级精化到光波波长，实现亚微米的距离分辨测量。

模间拍频合成波长法利用光频梳分立频谱的特性，直接产生合成波长链，不依赖外部辅助激光器，简化了光源结构。此外，可使用不同波长的拍波对目标进行并行测量，测量时间短。但是此方法并不能解决合成波长法对初始值的依赖性问题，不适用于待测距离未知的大尺寸绝对距离测量。

3）脉冲对准时间飞行法

2004年，美国实验天体物理联合研究所（Joint Institute for Laboratory Astrophysics，JILA）的华裔物理学家叶军（Jun Ye）提出了一种结合脉冲飞行时间测距原理和脉冲互相关干涉条纹辨析测距原理的绝对距离测量方法。其测量原理如图3.38所示。

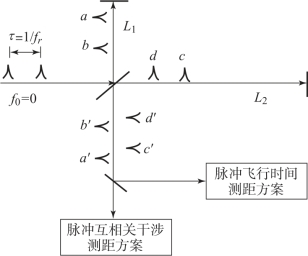
图3.38　脉冲飞行时间与互相关干涉联合测距法系统结构

图中，飞秒光频梳入射至迈克尔逊干涉测量系统，脉冲周期满足，参考臂和测量臂的长度分别为L1 和L2，a′、b′为参考臂的反射脉冲，c′、d′为测量臂的反射脉冲，探测光路由分光镜分为两路，分别进行时间飞行和相关分析的测量。对于未知距离的粗测是基于脉冲飞行时间测距原理。如图3.38所示，第一次测量时，光频梳重复频率设定为fr1，对应的脉冲间隔为τ1，激光脉冲序列经分光镜分别进入参考臂和测量臂，被反射镜反射后于分光镜处合束，测量臂和参考臂反射的脉冲到达探测器的时间间隔为Δt1。此时测量臂与参考臂之差（即待测距离）为

式中，n 为脉冲数。

同理，第二次测量时，调整脉冲重复频率为fr2，脉冲的间隔变为τ2，脉冲序列经参考臂和测量臂反射后到达探测器的时间间隔为Δt2。此时待测距离可以表示为(www.xing528.com)

由式（3.63）、式（3.64）以及已知的光频梳脉冲时间间隔τ1、τ2 和时间延迟Δt1、Δt2，即可确定脉冲数n 以及粗测距离值ΔL，此即为脉冲飞行时间法绝对距离测量。受限于光电传感器及信号处理速度，延迟时间测量的分辨率仅能达到3 ps，对应的距离粗测精度可达1 mm 左右。

在采用脉冲时间飞行法进行距离粗测之后，需要采用脉冲互相关法进一步实现对被测距离的精确测量，这个过程需要对光频梳的重复频率进一步调节，使得参考臂和测量臂反射回的脉冲能够相互干涉。此时光频梳的重复频率为fr3，脉冲间隔相应变为τ3。由图3.39可知，对重复频率连续调节可以得到测量臂和参考臂反射脉冲完全重合的情况，此时Δt3≈0，对应的待测距离为

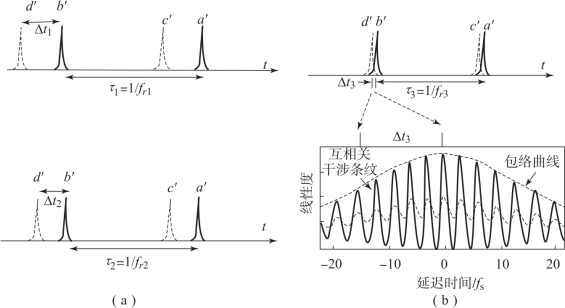
图3.39　脉冲飞行时间与互相关联合测距法原理示意图

（a）基于脉冲间隔扫描的飞行时间距离粗测；（b）基于脉冲互相关干涉条纹辨析的距离精测

在之前脉冲时间飞行法中已经将脉冲数n 确定，因此通过精确测量fr3得到τ3 即可对待测距离ΔL 进行精确计算。在实际的测量过程中，为抑制延迟时间测量分辨率对精测过程中确定脉冲序列重合点所带来的误差，精确地确定脉冲重合所对应的重复频率，通常如图3.39（b）所示，利用脉冲互相关干涉曲线的几个极大值进行曲线拟合，拟合曲线的最大值作为脉冲完全重合点。最终，使用该方法实现了10～106 m 测量范围且测距分辨率小于一个波长的测量结果。

非相干时间飞行法和相干条纹辨析相结合的测量方法为绝对距离测量开启了新思路，可以测量从几米到超过106 m 的任意距离，并具有亚波长的测量精度，对以后的飞秒脉冲激光器绝对距离测量的研究具有十分重要的指导意义。但是该方案的缺点是测量过程中要求对光频梳重复频率进行高精度的扫描，延长了测量时间，降低了数据的更新速率。在进行短距离测量时，需要对重复频率进行更大范围的调节。另外，光频梳重复频率稳定度以及偏置频率的相位误差稳定度都会导致脉冲干涉信号强度的降低，进而影响到测量精度，且此方案未考虑到空气折射率的影响，未考虑激光脉冲在空气中传播的色散和脉冲展宽问题，空气环境测量精度难以保证。

4）色散干涉法

韩国科学技术院（KAIST）的科学家Joo 和Kim 等人于2006年提出了光频梳色散干涉测距法。该方法的光路采用迈克尔逊干涉光路基本结构，图3.40示出了其测量原理图。

针对脉冲重合法对距离测量量程的限制，在色散干涉法系统中，利用F-P 腔进行光学滤波，能够穿过F-P 腔的光频梳只包含频率为滤波腔自由光谱区范围整数倍的梳齿，因此极大地增大了光学频率梳的剩余梳齿间距，随后再利用光栅将F-P 腔滤波后的光频梳中各频率成分进行空间分离，调整会聚透镜与线阵CCD 的位置，使得每一个频率成分分别对应CCD 上的一个像素点，以此来实现对光频梳特定梳齿的干涉测量相位，并利用波长和相位的关系得到最终的待测距离。这种方式利用色散的方式解除了各纵模之间的相位关系，将脉冲探测转化为直流干涉信号的探测，因此不受时域脉冲重合要求的限制，可在连续范围内实现绝对距离测量。

图3.40中，合光时参考臂和测量臂电场可分别表示为

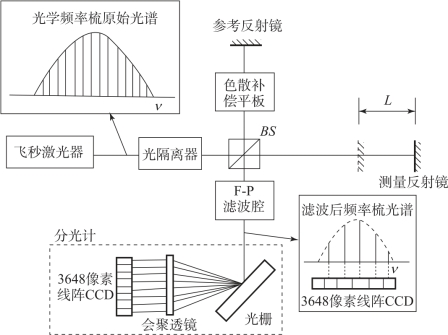
图3.40　光频梳色散干涉法测距原理图

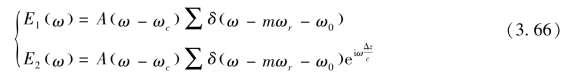
式中，Δz 为参考臂和测量臂的光程差。经色散元件分光后，不同频率的连续光在CCD 上不同像素点上干涉，干涉电场E （ω）=E1 （ω）+E2 （ω），CCD 上探测到的干涉强度I （ω）可表示为

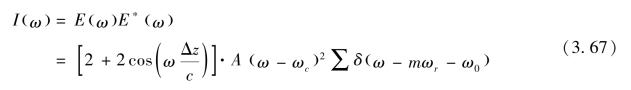
式中，为干涉信号的周期。

在计算距离时，首先对测得的干涉光谱进行傅里叶变换。由于函数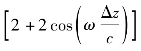的傅里叶变换包含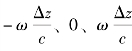三个频率分量，通过带通滤波选出频率分量并对其进行逆傅里叶变换。对逆变换得到的函数通过虚部与实部的除法求出相位，最后通过直线拟合求解斜率，得到待测距离。

使用色散干涉法进行绝对距离测量，将周期脉冲信号转化为不同频率的连续光干涉，有效地解决了脉冲对准时间飞行法量程的限制。理论上，在实现对光谱单纵模分辨的情况下，光频梳色散干涉法的固有量程为，并可以通过改变重复频率的方式实现量程拓展。但是受色散元件分光能力限制，实际应用中很难实现对单纵模的频率分辨，通常需要使用重复频率大于1 GHz 的固体飞秒激光器作为光源，使用F-P 腔滤波才能实现单纵模分辨，但此时出射光的功率会有很大的衰减，也会对绝对距离测量带来新的限制因素。

5）双光梳测距法

美国NIST 的研究人员提出采用两台重复频率略有差异的光频梳作为光源来进行绝对距离测量，这种方法利用重频差引起的游标效应实现脉冲之间的时域扫描，保证了对任意时刻脉冲的光学采样，从而解决了脉冲重合引起的量程受限问题。

双光梳测距的系统装置示意图见图3.41，两台光频梳锁定至经超稳腔稳频的窄线宽激光器上，其重复频率分别为fr+Δfr 和fr，使用重复频率为fr+Δfr 的光频梳的脉冲以时间间隔的形式记录半透半反镜与角锥之间的距离。经半透半反镜和角锥的反射脉冲与重复频率为fr 的脉冲在PBS 上合光，利用Δfr 的重频差实现对反射脉冲的线性光学采样，进而求出反射脉冲的峰值位置，进一步计算出待测距离。

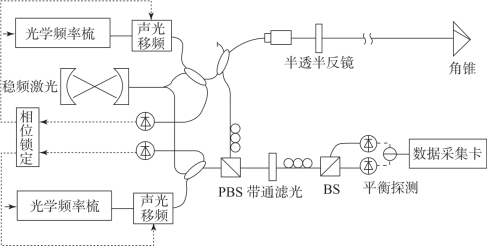
图3.41　双光梳绝对距离测量

在PBS 上合光时，半透半反镜反射光电场Eref （t）、角锥反射光电场Etar （t）以及采样光电场ELo （t）分别可以表示为

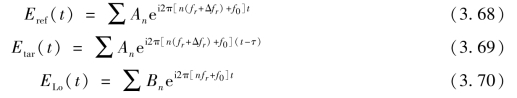
式中，An、Bn 为相应梳齿的强度；τ 为角锥反射信号相对于半透半反信号的时间延迟。式中假设两台光频梳的偏置频率均为f0，光谱中第一根纵模频率差为Δfr。此外，由于测量距离的变化，假设各电场的初始相位均为0。由式（3.68）～式（3.70）可知，参考信号与测量信号的互相关强度均包含一系列分布在0、fr、2fr 等附近间隔为Δfr 的拍频，通过低通滤波的方式选取零频附近的拍频，因此滤波之后的参考信号和测量信号互相关强度为

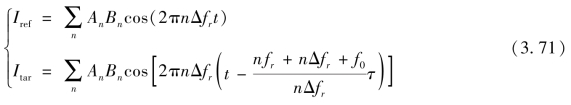
其中假设了光谱中第一根纵模频率差为Δfr，两台光频梳光谱中包含的纵模数量相同，通过测量两信号的相位差就可以计算出待测距离。对于第一根纵模频率差不为Δfr 的情况，相当于对Iref和Itar的频谱进行平移，不影响相位差的计算。对于光谱中纵模数量分别为NA 和NB的情况，受低通滤波的限制，n 的最大值为NA 和NB 中较小的数，同样不会影响相位差的计算。

通过对Iref和Itar进行傅里叶变换，求出相位谱φref和φtar。由式（3.71）可知，两个干涉信号的相位差为

其中，φ（nΔfr）代表第n 个拍频的相位。通过相位差φ 对Δfr 差分，得到相位变化斜率

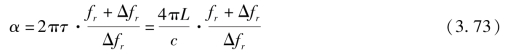
由式（3.73）可求出待测距离L。由于相位解调的方法只能求解半波长之内的距离，实际测量时先使用时间飞行法测量Iref和Itar的时间间隔，然后再使用傅里叶变换求解相位谱，得到半波长之内的精确结果。