合成波长法优化方案：合成波长技术解析

合成波长激光干涉测试技术是在小数重合法的基础上发展而来的。以双波长为例，设参与干涉测量的两束光的波长分别为λ1 和λ2（λ1>λ2），分别用这两个波长测量待测的距离L，可得

由此可以进一步推导出

式（3.31）与式（3.30）形式一致。令，ms=m2-m1，εs=ε2-ε1，则有

式中，λs 为两波长的合成等效波长，简称合成波长；ms 和εs 分别为λs 干涉级次的整数部分和小数部分。

两个不同波长（λ1 和λ2）单色波的电场表达式为根据波的叠加原理，合成波的电场表达式为

式中，

若令A=2a cos（ksz-ωst），则式（3.34）可以写作

表示合成波是一个频率为、振幅为A 的波，其振幅随着时间在-2A～2A 变化，振幅的调制频率为ωs，调制波的波长为。因此式（3.32）中的合成波的波长物理含义即为两个波长的拍频所得到的调制波的波长。图3.28给出两个单色波及其叠加所得到的合成波电场，可见，合成波的波长比任何一个单独的波长都要大很多。

图3.28　两个单色波的叠加

单个波长测量距离时满足

由于相位测量只能确定其小数部分，因此单个波长的测量范围被限制在以内，所以由于λ1 和λ2 的合成波λs 的波长比任何一个单独的波长都要大很多，因此测量的范围能够大幅增加。进一步，如果采用多个测量波长产生一个或多个大于单波长的合成波长，并以此作为新的测量标准时，干涉测量法的单值测量范围将被继续扩大。

合成波长链的形成就是用几个波长相近、间隔均匀的单波长进行适当的逐级组合，得到一个波长由小至大的波长链的过程。在两个单波长组成的合成波长的计算公式中，若比λ1、λ2都小，则λs 必然大于λ1、λ2。将λs 与其他单波长组成的合成波长再进行组合，就可以得到更高一级的合成波长，且该合成波长要比λs 大许多。这种组合可以继续进行下去，直到最后得到一个最高一级的合成波长。将该过程中得到的合成波长由小到大逐级排列，就会得到形状类似金字塔的合成波长链，塔顶是最高一级合成波长，塔底是零级合成波长，即单波长。针对具体的光源，可以采用与之适应的组合方式，以达到最好的测量效果。

在待测距离为L 的双光束干涉仪中，采用N 个波长进行测量，可以得到测量方程组

式中，mi（i=1，2，…，N）为不同波长干涉级次的整数部分；εi（i=1，2，…，N）为不同波长干涉级次的小数部分；L 为待测的光程差或距离。

方程组（3.37）中L 与mi（i=1，2，…，N）为未知，εi（i=1，2，…，N）可以直接测量获得，因此N 个方程共有N+ 1 个未知数。方程组（3.37）有无穷多个解，但是mi（i=1，2，…，N）只能取正整数，因此该方程组的解具有周期性。令波数，则方程组（3.37）可以改写为

取整数权因子Ai 来求解3.38 式（Ai 可取零和正负整数），以保证mi 在处理后仍然保持整数，由此可得

(www.xing528.com)

因此由式（3.39）可得

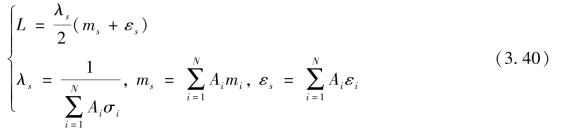
式（3.39）形式与式（3.30）一致，因此称λs 为合成波的波长。不同的Ai 组合会给出不同的合成波长λs 的值，从而构成了解的周期结构。由两个波长构成的空间频率为

依此类推，三个波长构成的空间频率为

N 个波长所构成的空间频率为

式中，（i=1，2，…，N）为二项式系数；ΓN-1=（ΓN）-1为利用方程组确定的长度的空间周期。

综合考虑式（3.40）和式（3.43）可知，使得λs=Γ-1N 的条件是

根据上述讨论，利用多个波长可以组合成比任意一个单波长大得多的合成波长。如图3.29所示，可以形成一个合成波长链，先由最高级次的合成波确定一个最初的初测值，然后再根据级次依次减小的合成波逐步得到精确值。

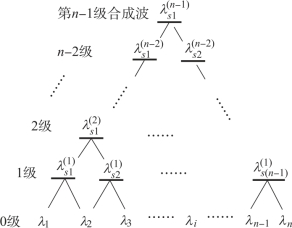
图3.29　多个波长合成波长链

逐级精化过程就是根据粗测值从合成链最高一级合成波长开始逐级提高被测长度测量值的精度，实现高精度测量。在此逐步提高测量精度的过程中需要保证整数级次的唯一性，即

式（3.45）两式相减可得

式中，δ（εi-1）为小数级次的测量误差。需要保证整数级次的唯一性要求式（3.46）中，因此可得

式中，ΔLi 为初测的不确定度；λs（i-1）为本次测量的合成波长；δLp 为本次测量的小数级次带来的不确定度。

当满足式（3.47）时，ms（i-1）的值可以表示为

由式（3.48）计算得到的整数级次以及相位计测量得到的小数级次εs（i-1）即可计算出被测距离。

每一级次的测量不确定度来自其小数级次部分的不确定度，因此由式（3.48）可以推导出采用相邻两级合成波长进行测量时需要满足的“级间过渡条件”为

式（3.49）是多波长合成波长链相邻两个级次间的测量能够连续，从而实现进一步提高测量精度的条件，也是保证测量结果唯一性的条件。多波长绝对距离测试技术应用于测量物体表面形状、台阶结构、圆度等短程测量，其由环境变化带来的误差较小。如要进行大尺度范围内的测量，采用多个单波长组成程度逐级增加的合成波长链，依据初测值和各干涉级次小数相位从最高合成波长开始逐级求解，并利用相应的整小数结合的方法确定待测距离。