莫尔测量技术的原理和应用

1.几何光学原理

要形成莫尔条纹至少需要包括两块光栅，其中较长的作为光栅尺，又称为主光栅，较短的作为指示光栅，两者组成一对光栅副。如果所用的光源为非相干光源，光栅为栅线间距（栅距）较大的光栅，一般来说，栅距不应小于0.01 mm，称为黑白光栅。而光栅副栅线面之间间隙较小时，通常可以按照光是直线传播的几何光学原理，利用光栅栅线之间的遮光效应来解释莫尔条纹的形成，并推导出光栅副结构参数与莫尔条纹几何图形的关系。更小栅距的光栅形成的莫尔条纹一般是衍射干涉形成的。下面讨论黑白光栅的性质。

设光栅对的栅线夹角为θ，取栅线竖直的主光栅A 的零号栅线为y 轴，垂直于主光栅A的栅线的方向为x 轴。倾斜了θ 角的指示光栅B 的零号栅线与y 轴的交点为原点，如图2.22所示。

图2.22　黑白光栅莫尔条纹形成原理

从图2.22容易看出，主光栅与指示光栅各栅线交点的连线即构成了莫尔条纹。如果主光栅栅线序列用i=1，2，3，…表示，指示光栅栅线序列用j=1，2，3，…表示，则两光栅栅线的交点为[i，j]。莫尔条纹1 由两光栅各同栅线交点[0，0]，[1，1]，…的连线构成。又设主光栅A 的栅距为P1，指示光栅B 的栅距为P2。由图中看出，主光栅A 的栅线方程为

指示光栅B 的栅线j 与x 轴交点的坐标为

莫尔条纹1 是由A、B 两光栅i=j 栅线的交点连接而成，所以其条纹的方程为

莫尔条纹1 的斜率为

莫尔条纹1 的方程可表示为

同样可以求得莫尔条纹2 和3 的方程分别为

由式（2.98）、式（2.99）、式（2.100）可以得出结论：莫尔条纹是周期函数，其周期T=P2/sin θ。它也被称为莫尔条纹的宽度B。当P1=P2时，由式（2.98）可得

就得到横向莫尔条纹。横向莫尔条纹与x 轴的夹角为θ/2。实用中两光栅的夹角θ 很小，因此可以认为莫尔条纹几乎与y 轴垂直，如图2.23（a）所示。

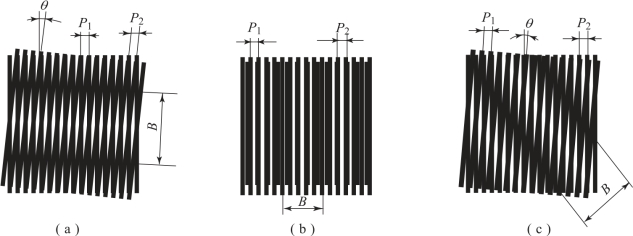
图2.23　不同形式的长光栅莫尔条纹

（a）横向莫尔条纹；（b）纵向莫尔条纹；（c）斜向莫尔条纹

当θ≠0，而P2=P1cosθ 时，就得到了严格的横向莫尔条纹。因此，当两光栅栅距不同时，总能找到一个θ 角，得到横向莫尔条纹。

当θ=0，而P2≠P1 时，就得到如图2.23（b）所示的纵向莫尔条纹。

其他情况都是斜向的莫尔条纹，如图2.23（c）所示。

在计量光栅中取P1=P2，且栅线夹角很小。当主光栅相对于指示光栅移动一个栅距时，莫尔条纹就移动了一个条纹间隔。在某一点观察时，能看到光栅的移动，某点的透过光强作明暗交替变化，这就是莫尔条纹的调制作用。莫尔条纹把光栅位移信息转换成光强随时间变化的信号。在空间上光栅移动的周期为P1，而莫尔条纹移动的周期是B。可见，莫尔条纹有放大作用，放大系数K=B/P1。虽然光栅栅距很小，但是它移动一个栅距，则莫尔条纹一个周期在空间尺寸就要大几百倍，这样就便于安装光电测量头进行测量。此外，莫尔条纹是由一系列光栅栅线交点组成的，光电器件接收莫尔条纹的透过能量。这样既能得到足够的光能量，有很高的信噪比，而且还能对栅线的工艺误差有平均作用，平均的结果使栅线误差在测量中的影响减小。

2.衍射原理

单纯利用几何光学原理，不可能说明许多在莫尔测量技术中出现的现象。例如，在使用相位光栅时，这种光栅处处透光，它对入射光波的作用仅仅是对其相位进行调制，然而，利用相位光栅亦能产生莫尔条纹，这就不可能用栅线的遮光作用予以说明；当使用细栅距光栅时，在普通照明条件下就很容易观察到彩色衍射条纹。两块细栅距光栅叠合形成的莫尔条纹中，往往会出现暗弱的次级条纹，这些现象必须应用衍射原理才能解释；在莫尔测量技术中用到的光栅自成像现象也是无法用几何光学原理解释的。

使用衍射原理分析莫尔条纹原理主要分为两个步骤：①入射光在光栅副上的衍射；②衍射光的干涉。

1）光栅副的衍射

由物理光学可知，当一束单色平面波入射到光栅G1上时，将发生衍射，产生方向不同的各级平面衍射光，如图2.24所示。若在这块光栅后面再放置一块光栅，这两块光栅便形成一光栅副。一束单色平行光先入射到第一光栅上，由第一光栅产生的每一级的衍射光对第二光栅来说又是一入射光束，此入射光束通过第二光栅后又将产生不同级的衍射光束。因此，由光栅组合出射的每一衍射光束应由它在两个光栅上的两个衍射级序数表示。如果第一光栅G1的第n 级衍射光经G2后产生第m 级衍射光，此衍射光束的级序可表示为（n，m）。

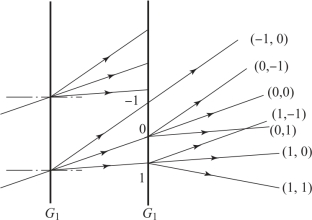
图2.24　双光栅的衍射级

若G1最多可产生N 级衍射光，G2最多可产生M 级衍射光，则总出射光束为N ×M。尽管衍射光束有N×M 个，但衍射光束的方向远小于N ×M 个，在G1和G2相同时，衍射级序满足n+m=r 的出射光束的方向总是相同的，这一方向称为光栅副的第r 级方向，在这个方向上包含多个衍射光束。当光栅副中G1和G2的栅距相差很小并且栅线夹角θ 很小时，在同一级组光束中，各光束的出射方向基本相同。

2）衍射光的干涉

光栅副衍射光有多个方向，每个方向又有多个光束，它们之间相互干涉形成的条纹很复杂，形成不了清晰的莫尔条纹。可以在光栅副后面加透镜L，在透镜焦点处用一光阑只让一个方向的衍射光通过，滤掉其他方向的光束，以提高莫尔条纹的质量，如图2.25所示。

(www.xing528.com)

图2.25　光栅副衍射光的干涉

在同一方向上的光束中，由于它们的衍射级次不同，相位和振幅不同，它们相干的结果仍很复杂。通常光栅低级次衍射的光能量要比高级次大得多，因此实际应用中常选用衍射级序数r=1 的一级组工作。至于在一级组中，两相干衍射光束的选定则应按照等效衍射级次最低的原则确定。所谓等效衍射级次是指每一束光两衍射级次绝对值之和，衍射级次越低则光能量越大。例如，在r=1 的一级组中，（0，1）和（1，0）这两束光的能量最大，为一级组中主要分量，一级组的干涉图主要由此两分量相干决定。

由一级组（0，1）和（1，0）两光束相干所形成的光强原理分析的结果较理想。但是在考虑同一组中各衍射光束干涉相加的一般情况下，莫尔条纹的光强分布不再是简单的余弦函数。通常，在其基本周期的最大值和最小值之间出现次最大值和次最小值，即在其主条纹之间出现次条纹、伴线。在许多场合，例如，对莫尔条纹信号做电子细分时要求莫尔条纹光强分布的数学表达式为较严格的正弦或余弦函数。此时，应当采用空间滤波或者其他措施，以除去莫尔条纹光强变化中的谐周期变化成分。

3.傅里叶分析方法

莫尔条纹的形成基于光栅副的叠加作用。光栅可被看作一种对入射光波振幅和相位进行调制的装置。在数学上，光栅可被描述为一种空间周期函数，由此，可用傅里叶分析的方法分析光栅的特性及讨论莫尔条纹的形成原理。傅里叶分析方法可分析莫尔条纹的方向和宽度，又可计算出莫尔条纹的光强分布，并且分析过程灵活、简便。

1）单光栅的透射特性及其傅里叶表达式

a）标准表达式

设X，Y 平面为光栅栅线所在的平面，取直角坐标如图2.26（a）所示。设X 轴垂直于栅线的方向，栅线结构对称于Y 轴分布。此透射光栅透过率的傅里叶级数表达式为

式中，f 为光栅的空间频率，f=1/P，P 为栅距；An为傅里叶系数。

式中，α 为光栅的占宽比，α=a/P，即光栅上透光的孔宽a 与栅距P 之比。

b）平移光栅表达式

设光栅栅线沿X 轴方向平移s，如图2.26（b）所示。此时，光栅透过率的傅里叶级数为

c）旋转光栅表达式

设光栅绕垂直光栅自身平面的轴转动θ 角，如图2.26（c）所示，光栅透过率的傅里叶级数表达式为

图2.26　单光栅投影

（a）光栅透过率分布；（b）光栅平移；（c）光栅旋转

2）莫尔条纹的光强分布

设G1和G2两个光栅的空间频率分别为f1=1/P1，f2=1/P2。G2为旋转平移光栅，G1 和G2的透过率傅里叶级数分别为

当G1与G2叠合，两栅间无间隙或间隙很小时，其透过率为

如果入射光栅副G1 和G2 的入射光强为I0（x，y），出射光强为I（x- s，y），取m=-n，则

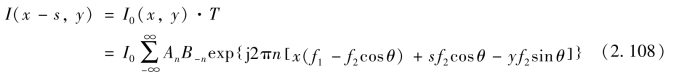
已知两个不同频率的正弦波以加或乘的形式叠加时，产生和频项和差频项。任意光栅均可视为具有一定空间频率的周期性结构，两光栅叠合时，其组合透过特性可表达为两个具有不同空间频率函数的乘积，因此，即产生空间频率概念上的和频与差频（拍频）项。一般认为，莫尔条纹的空间频率低于原光栅的空间频率，所以莫尔条纹即为两光栅叠合产生的拍频部分，莫尔条纹的空间频率就是拍频频率，空间频率最低（周期最大）的部分即为莫尔条纹的基波。莫尔条纹的形状由基波决定，其他谐波频率成分则只影响莫尔条纹的光强分布。

由以上分析，令式（2.108）中f1-f2cosθ=Fx，-f2sin θ=Fy，则式（2.108）变为

式中，Fx和Fy为莫尔条纹在X，Y 轴上的分量。

用傅里叶分析方法分析两光栅叠合所产生的莫尔条纹时，可先将两光栅的频率分别在所选定的坐标轴上分解，然后在相应的坐标轴上作它们的差频，从而得到莫尔条纹在各个坐标轴上的频率分量Fx和Fy，则莫尔条纹的频率和方位分别为

如果两光栅的频率分别为f1=10 lp/mm，f2=9 lp/mm，纵向莫尔条纹（θ=0）的频率为

f=f1-f2=10-9=1

莫尔条纹宽度W=1/f=1 mm。

可见，在分析莫尔条纹的频率（或周期）和方位，而不考虑其强度分布时，用空间频率的概念分析更为方便、简单。